백준 10830 행렬 제곱[JAVA]

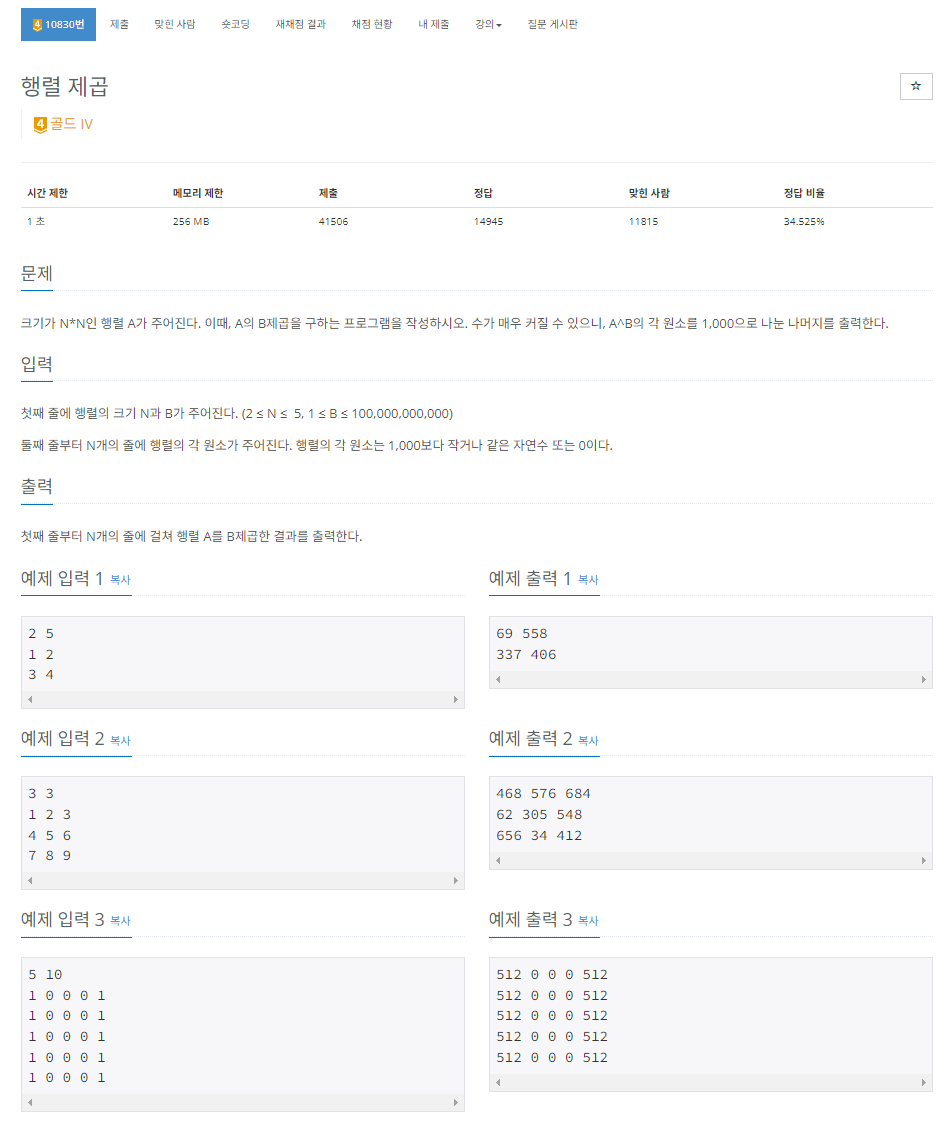
문제 해석

• 문제는 백준2740행렬 곱셈문제와 비슷한 문제로 행렬의 제곱을 구하면 된다.
• 첫번째 줄에서 행렬(NxN)의 크기인 N과 제곱 횟수 B를 입력받는다. ( 2 <= N <= 5, 1 <= B < 100,000,000,000)
• 두번째 줄부터는 N개의 줄을 거쳐 행렬의 원소를 입력 받는다. (단, 0 < 원소 < 1,000)
• 행렬 A를 B제곱한 행렬을 뽑아낸 다음 각 요소를 1000으로 나눈 값을 출력하면 된다.
• 행렬 A를 B제곱한다는 것은 자기 자신을 B번 곱한다는 것이므로 전 포스트였던 행렬 곱셈과 비슷하다.
  

코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    final static int MOD = 1000;
    static int[][] originA;
    static int N;
    public static void main(String[] args) throws IOException {
        BufferedReader br =  new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        StringBuilder sb = new StringBuilder(); //출력 값 쌓아두고 한꺼번에 출력하기 위해
        
        N = Integer.parseInt(st.nextToken()); //행렬 A의 NxN
        long B = Long.parseLong(st.nextToken()); //행렬 A의 제곱해야하는 수

        originA = new int[N][N]; //행렬 A

        for(int i = 0; i < N; i++) { //행렬 A 값 넣기
            st = new StringTokenizer(br.readLine(), " ");
            for (int j = 0; j < N; j++) {
                //만약 1제곱의 경우 그대로 나오게 되는데 만약 행렬 A의 원소중에 1000인 원소가 있다면 오답이 된다.
                // => 그러한 이유로 1000을 기존 원소에 1000을 나눈 나머지로 초기값
                originA[i][j] = Integer.parseInt(st.nextToken())%MOD;
            }
        }

        br.close();

        int[][] result = pow(originA, B);

        for(int i = 0; i < N; i++){
            for(int j =0 ; j < N; j++){
                sb.append(result[i][j]).append(" ");
            }
            sb.append("\n");
        }

        System.out.println(sb);

    }

    public static int[][] pow(int[][] A, long exp){ //파라미터 행렬(A), 지수(exp)
        if(exp == 1L){ //지수가 1이라는 것은 이제 더이상 제곱할게 없음!
            return A;
        }

        //지수를 분할하여 계산! (두번 계산하는 것을 방지)
        int[][] divid = pow(A, exp/2);

        //해당 분할 계산한 행렬을 두개 파라미터로 보내서 곱을 진행 
        divid = multiPly(divid, divid);
        
        if(exp % 2 != 0L){ //만약 지수가 홀수라면 초기값을 한번 더 곱해줘야 함
            divid = multiPly(divid, originA);
        }

        return divid;
    }

    public static int[][] multiPly(int[][] A1, int[][] A2){ //행렬 곱
        int[][] gop = new int[N][N];

        for(int i = 0; i < N; i++){
            for(int j = 0; j < N; j++){
                for(int k = 0; k < N; k++){
                    gop[i][j] += A1[i][k] * A2[k][j];
                    gop[i][j] %= MOD;
                }
            }
        }
        return gop;
    }
}

결과

느낀 점

처음에는 곱셈을 여러번 진행하다가 분할정복이라는 카테고리에 맞게 분할 후 곱셈을 했더니 큰 어려움은 없이 풀 수 있었다.