문제 해석
-
바이토닉 수열은 증가 -> 감소의 형태를 띤 수열을 의미한다.
-
하나의 수열을 가지고 바이토닉 수열로 만들어서 가장 긴 바이토닉 수열을 만들려면 왼 -> 오, 오 -> 왼로 각각의 인덱스별 증가하는 수열의 길이 값을 구해서 왼 -> 오, 오 -> 왼의 배열을 각 인덱스의 길이 값을 더함으로써 긴 바이토닉 수열을 만들 수 있다.
-
말로 정리하기엔 이해의 어려움이 있을 수 있어서 아래에서 사진과 글로 설명하고자 한다. (저도 글로만 정리하기에 완벽하게 설명을 못할 것 같은...)
-
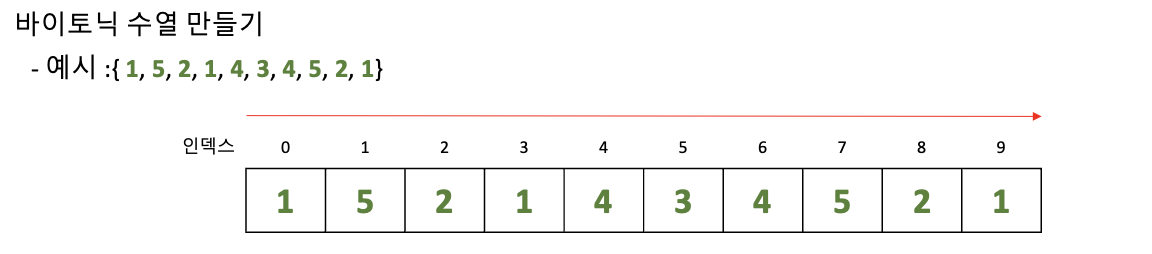
일단 아래와 같이 수열이 주어졌다고 치자.
-
각 인덱스의 값들의 증가하는 수열 길이(왼->오로 증가하는 수열)를 구하면, 아래와 같은 수열이 생긴다.
인덱스 0>> {1} -> 길이 1
인덱스 1>> {1, 5} -> 길이 2
인덱스 2>> {1, 2} -> 길이 2
인덱스 3>> {1} -> 길이 1
인덱스4>> {1, 2, 4} -> 길이 3
인덱스5>> {1, 2, 3} -> 길이 3
인덱스6>> {1, 2, 3, 4} -> 길이 4
인덱스7>> {1, 2, 3, 4, 5} -> 길이 5
인덱스8>> {1, 2} -> 길이 2
인덱스9>> {1} -> 길이- 왼->오로 증가하는 인덱스별 길이 수열을 왼오수열이라고 치자.

- 다음은 오->왼으로 증가하는 수열의 각 인덱스별 길이 수열 오왼수열을 만들어야 한다.
- 왼->오와 반대로 증가방향의 화살표가 거꾸로다.
- 즉, 인덱스 9 -> 인덱스 0의 순서로 길이를 구해야한다.

인덱스9>> {1} -> 길이 1
인덱스8>> {1, 2} -> 길이 2
인덱스7>> {1, 2, 5} -> 길이 3
인덱스6>> {1, 2, 4} -> 길이 3
인덱스5>> {1, 2, 3} -> 길이 3
인덱스4>> {1, 2, 3, 4} -> 길이 4
인덱스3>> {1} -> 길이 1
인덱스2>> {1, 2} -> 길이 2
인덱스1>> {1, 2, 3, 4, 5} -> 길이 5
인덱스0>> {1} -> 길이 1
-
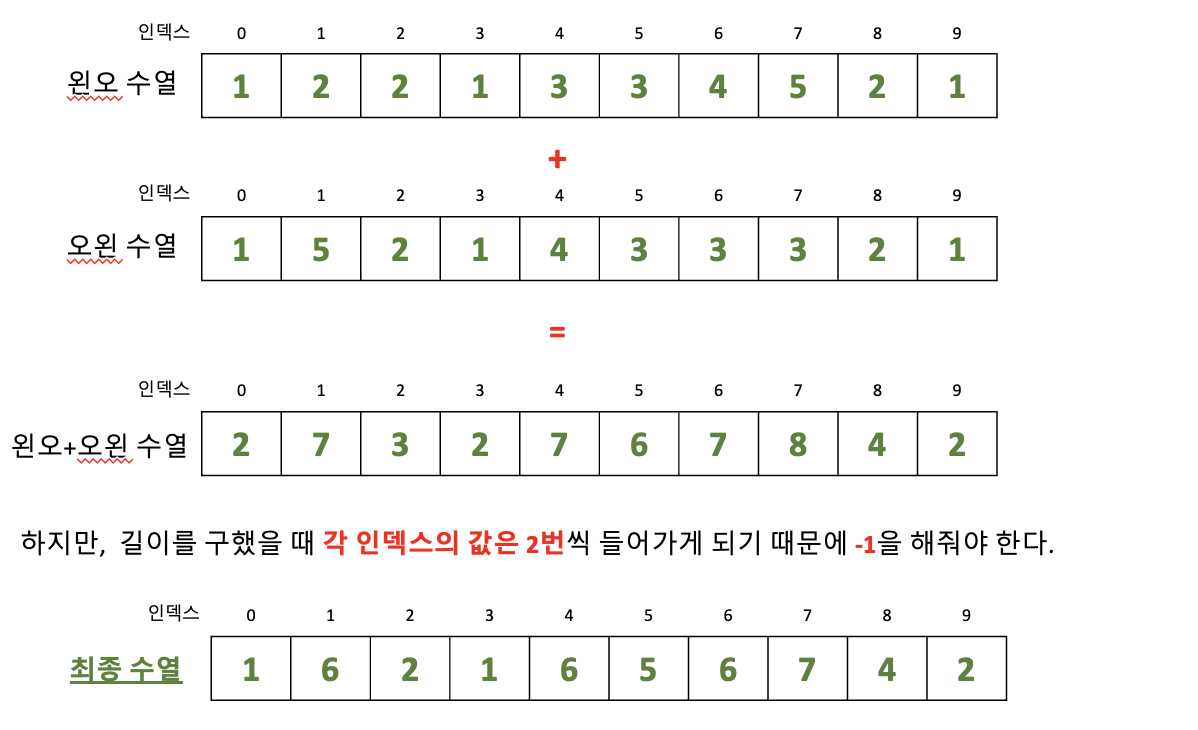
이렇게 왼오수열과 오왼수열을 더했다면 각 인덱스별로 서로 더해주면 된다. (각 인덱스의 값들은 2번씩 들어가므로(중복) -1을 해줘야한다.)
-
이런식으로 구해서 가장 긴 바이토닉 부분 수열의 길이는 7이 된다.
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
static int[] arr;
static Integer[] dp_right; //왼->오 수열
static Integer[] dp_left; //오->왼 수열
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
arr = new int[N];
dp_right = new Integer[N];
dp_left = new Integer[N];
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for(int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// 각각의 위치에 해당하는 길이를 구함
for(int i = 0; i < N; i++) {
solution_right(i);
solution_left(i);
}
int max = -1; //최솟값(-1은 나올 수 없는 구조이기 때문에 초기값 -1)
// 최댓값 찾는 코드
for(int i = 0; i < N; i++) {
max = Math.max(max, (dp_right[i]+dp_left[i]-1));
}
System.out.println(max);
br.close();
}
//왼->오의 각 인덱스별 수열 길이 찾기
static int solution_right(int depth) {
// 조회하지 않는 것일 경우
if(dp_right[depth] == null) {
dp_right[depth] = 1; // 1로 초기화
// 현재 위치보다 작은 값들을 찾고 카운트해서 넣는 방식
for(int i = depth - 1; i >= 0; i--) {
if(arr[i] < arr[depth]) {
dp_right[depth] = Math.max(dp_right[depth], solution_right(i) + 1);
}
}
}
return dp_right[depth];
}
//오->왼의 각 인덱스별 수열 길이 찾기
static int solution_left(int depth) {
// 조회하지 않는 것일 경우
if(dp_left[depth] == null) {
dp_left[depth] = 1; // 1로 초기화
// 현재 위치보다 작은 값들을 찾고 카운트해서 넣는 방식
for(int i = depth + 1; i < dp_left.length; i++) {
if(arr[i] < arr[depth]) {
dp_left[depth] = Math.max(dp_left[depth], solution_left(i) + 1);
}
}
}
return dp_left[depth];
}
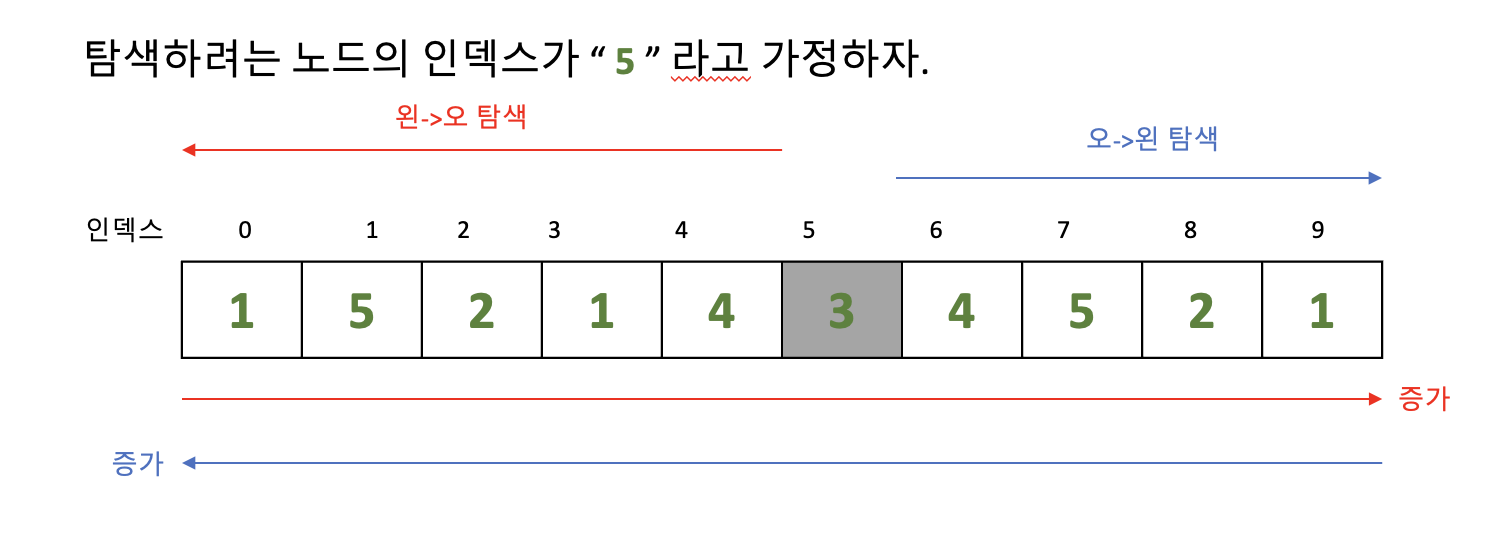
}- 왼->오의 경우 기존 방식대로 탐색하려는 노드의 이전의 노드로 순서대로 조회하여 수열을 구하면 된다.
- 오->왼의 경우 기존 방식과 약간 다르게 탐색하려는 노드의 이후의 노드로 순서대로 조회하여 수열을 구하면 된다.
- 사진으로 설명하면 아래와 같다.
결과

느낀점
- 문제를 이해하는데 시간이 오래 걸렸다... 전에 풀었던 문제에서 살짝만 추가하면 되는 문제인데도 헤맸다...
