문제 해석
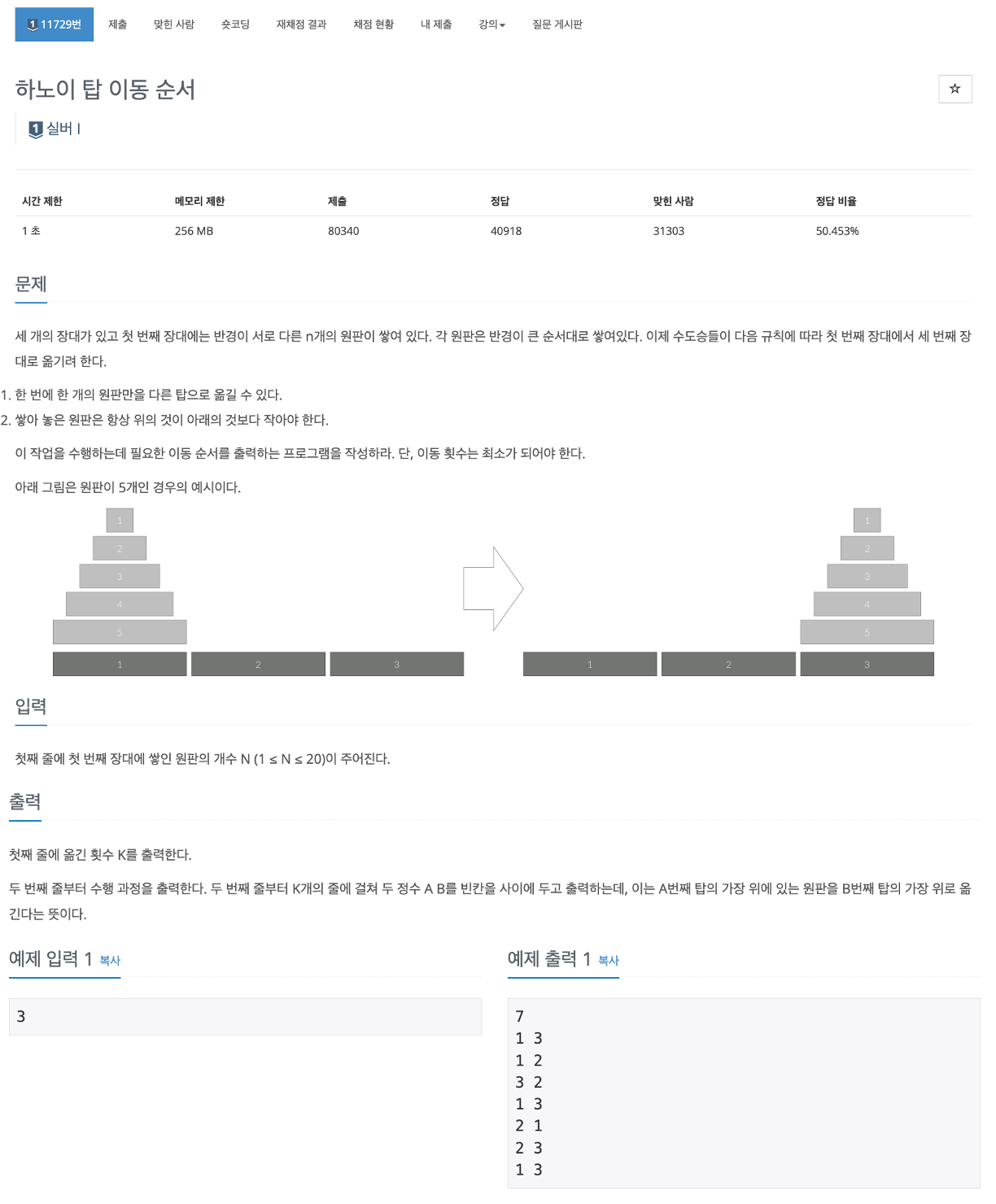
- 입력 값은 단 하나이다. 장대에 쌓이는 원판 개수(N)이다.
- 해당 원판이 장대1에서 위에서부터 아래로 1 2 3 4 5으로 쌓여 있다. 이 원판 순서 그대로 장대3으로 옮기면 된다. (장대2는 사용해도 된다)
- 그리고 출력 값으로는 첫번째 줄에 옮긴 횟수(최소여야함) K를 출력하고 그 다음 줄부터는 A B의 값을 사이에 공백을 두고 출력하는데 A번째(장대 숫자) 탑의 가장 위에 있는 원판을 B번째(장대 숫자) 탑의 가장 위에 올린다는 의미다. 즉 A와 B는 장대의 숫자로 생각하면 된다. 그렇게 K번째까지 출력한다.(A B의 형태로)
하노이의 최소 이동 수 구하는 방법
[초기 값] 위 ~ 아래
장대1 : 1 2 3 4 5
장대2 :
장대3 :
[얻고자 하는 결과 값] 위 ~ 아래
장대1 :
장대2 :
장대3 : 1 2 3 4 5
하노이 법칙에 따라 정리하자면, 작은 숫자 위에 큰 숫자가 오지 못한다.
그렇기 때문에 장대1에 있는 가장 아래 값 5(가장 큰)이 장대3에 가려면,
장대1의 1 2 3 4는 장대2에 가야하고 hanoi(N-1)번
장대1의 5는 장대3에 가니까 1번
그 후 장대2에 있는 1 2 3 4는 장대3에 가야하므로 hanoi(N-1)번
총 횟수는 2Xhanoi(N-1) + 1이 된다.
예시로 공식을 만들면,
원판 = 1
[초기 값]
장대1 : 1
장대2 :
장대3 :
[수행]
장대1 :
장대2 :
장대3 : 1
=> 총 1회
원판 = 2
[초기 값]
장대1 : 1 2
장대2 :
장대3 :
[수행]
장대1 : 2
장대2 : 1
장대3 :
장대1 :
장대2 : 1
장대3 : 2
장대1 :
장대2 :
장대3 : 1 2
=> 총 3회
원판 = 3
[초기 값]
장대1 : 1 2 3
장대2 :
장대3 :
[수행]
장대1 : 2 3
장대2 :
장대3 : 1
장대1 : 3
장대2 : 2
장대3 : 1
장대1 : 3
장대2 : 1 2
장대3 :
장대1 :
장대2 : 1 2
장대3 : 3
장대1 : 1
장대2 : 2
장대3 : 3
장대1 : 1
장대2 :
장대3 : 2 3
장대1 :
장대2 :
장대3 : 1 2 3
=> 총 7회
원판 = 4
[초기 값]
장대1 : 1 2 3 4
장대2 :
장대3 :
[수행]
장대1 : 2 3 4
장대2 : 1
장대3 :
장대1 : 3 4
장대2 : 1
장대3 : 2
장대1 : 3 4
장대2 :
장대3 : 1 2
장대1 : 4
장대2 : 3
장대3 : 1 2
장대1 : 1 4
장대2 : 3
장대3 : 2
장대1 : 1 4
장대2 : 2 3
장대3 :
장대1 : 4
장대2 : 1 2 3
장대3 :
장대1 :
장대2 : 1 2 3
장대3 : 4
장대1 :
장대2 : 2 3
장대3 : 1 4
장대1 : 2
장대2 : 3
장대3 : 1 4
장대1 : 1 2
장대2 : 3
장대3 : 4
장대1 : 1 2
장대2 :
장대3 : 3 4
장대1 : 2
장대2 : 1
장대3 : 3 4
장대1 :
장대2 : 1
장대3 : 2 3 4
장대1 :
장대2 :
장대3 : 1 2 3 4
=> 총 15회
원판 = 1 총 1회 [2^1 - 1 = 1]
원판 = 2 총 3회 [2^2 - 1 = 3]
원판 = 3 총 7회 [2^3 - 1 = 7]
원판 = 4 총 15회 [2^4 - 1 = 15]
규칙을 찾아 공식으로 바꾸면 2^N-1인 것을 확인할 수 있다!!
코드
import java.io.*;
public class Main {
static StringBuilder sb;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
sb = new StringBuilder();
int N = Integer.parseInt(br.readLine()); //원판의 개수
sb.append((int) (Math.pow(2, N)-1)).append("\n");
hanoi(N, 1, 2, 3);
br.close();
System.out.println(sb);
}
//hanoi 솔루션 메소드
// 파라미터 : 원판 개수(N), 시작 공간(start), 임시 공간(tmp), 목적지(to)
static void hanoi(int N, int start, int tmp, int to){
//이동할 원판의 개수가 1개면 start to 출력하면됨(차피 1개니까 로직 처리X)
if(N == 1){
sb.append(start + " " + to + "\n");
return;
}
/*
hanoi(N, start, tmp, to);
원판이 3이라고 가정하면,
(1)-1 hanoi(2, 1, 3, 2);
(1)-2 hanoi(1, 1, 2, 3);
** if N=1 print("1 3")
(2)-2 ** print("1 2");
(3)-2 hanoi(1, 3, 1, 2);
if N = 1 ** print("3 2");
(2)-1 ** print("1 3");
(3)-1 hanoi(2, 2, 1, 3);
(1)-2 hanoi(1, 2, 3, 1);
if N = 1 ** print("2 1");
(2)-2 ** print("2 3");
(3)-2 hanoi(1, 1, 2, 3);
if N = 1 ** print("1 3");
*/
// start -> to로 옮긴다고 가정하면
//(1) N-1까지는 tmp로 옮긴다.(start에 있는 요소들)
hanoi(N-1, start, to, tmp);
//(2) 1개(숫자 N자체; 가장 큰 숫자)를 start -> to로 이동한다.
sb.append(start+" " + to + "\n");
//(3) N-1을 tmp -> to로 옮긴다.(중간에 있는 것 N-1까지 옮긴 것을 to로)
hanoi(N-1, tmp, start, to);
}
}
결과

느낀 점
- 생각하면 간단한 문제인데 수행 순서(?)를 생각했을 때 머리가 복잡해져서 어이없지만 꽤 오래걸렸다.
