백준 1193 분수 찾기[JAVA]

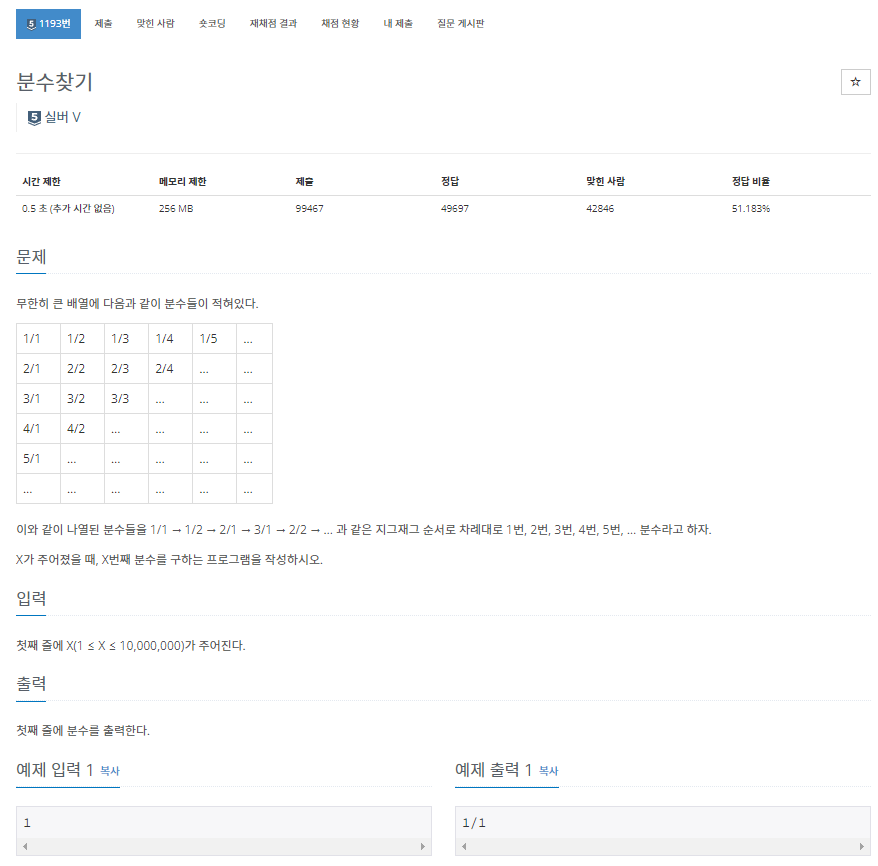
문제 해석

• 문제 자체는 이해하기 쉬운 문제이지만, 구현이 좀 어렵다.(개인적으로)

• 다음 배열(2차원 배열)에 아래처럼 적혀져 있다.
  

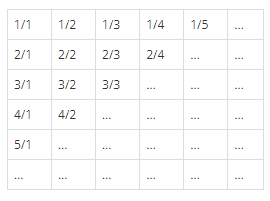
• 이 나열된 분수들은 지그재그식으로 순회하는데, 어떤 식이냐면 1/1은 위쪽방향으로 순회하고, 그 다음 대각선인 1/2, 2/1은 1/2 -> 2/1 방향(아래방향)으로 순회한다.

• 그에 관한 그림은 아래에 있다.

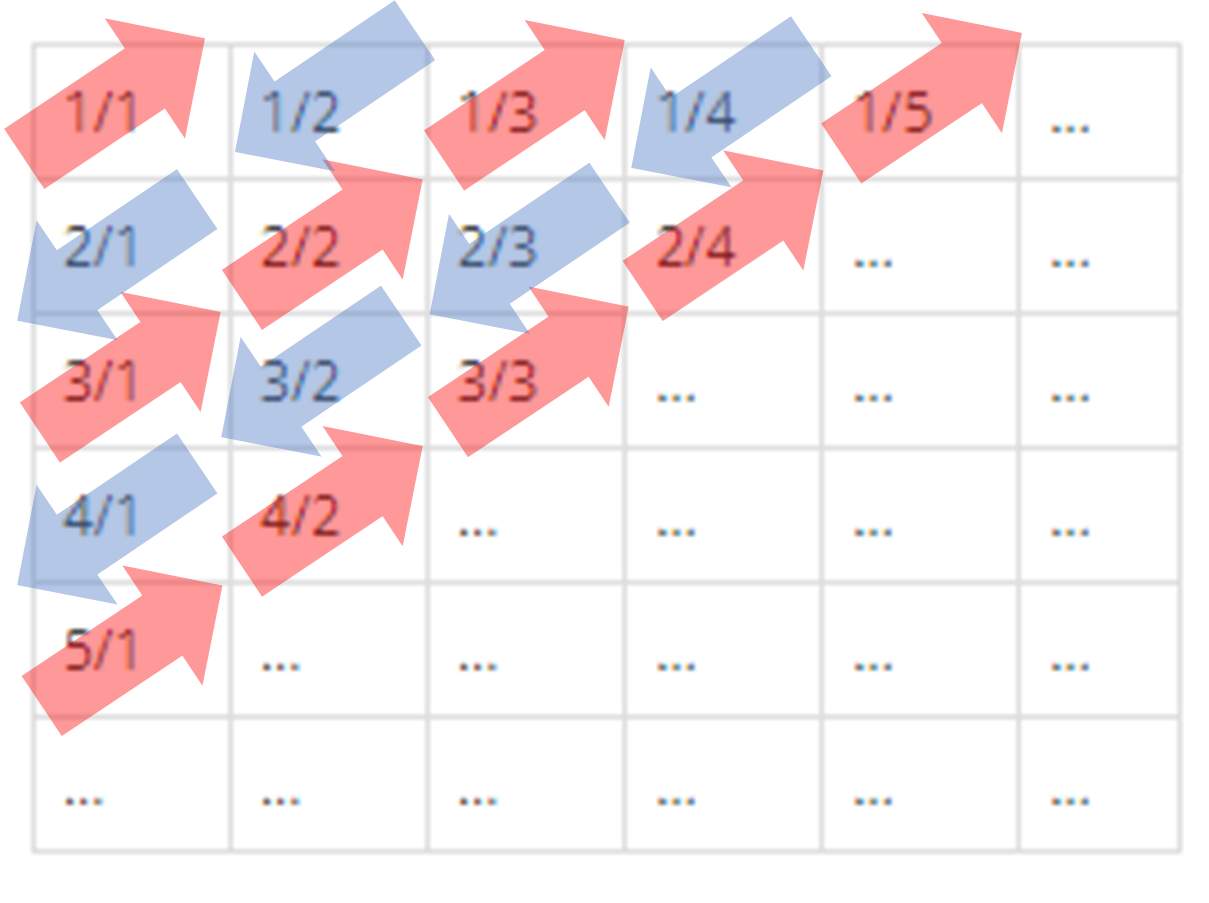
-> 규칙성을 찾으면 아래와 같다.

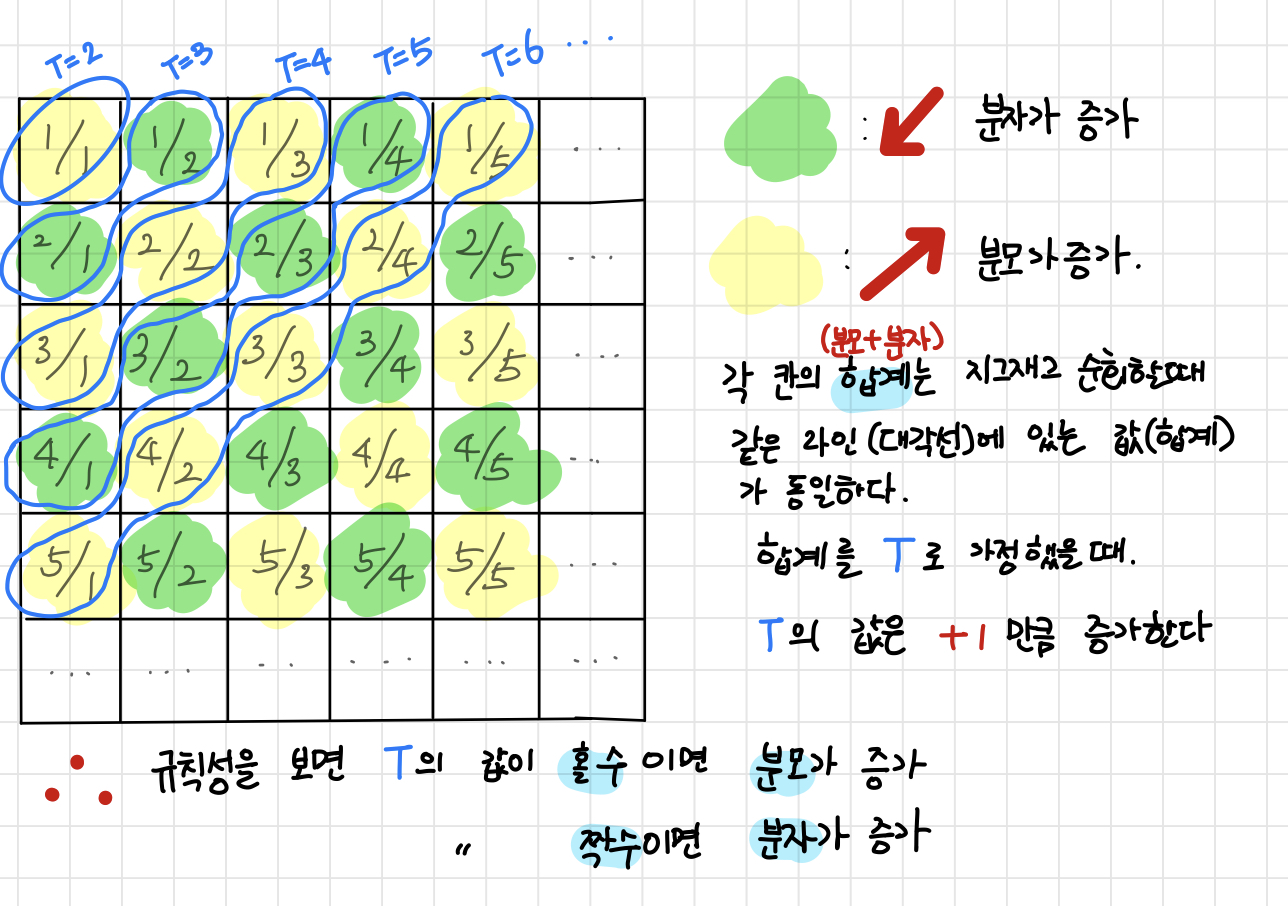
-> 다시말해 콘솔로부터 순서는 다음과 같은데, 콘솔로부터 X(몇번째 분수인지)를 입력받아 해당 분수를 출력하면 되는 문제이다.

문제 다시 정리

• T 가 짝수이고, 대각선 칸의 개수가 홀수 일 때는 위 방향 ( ↗︎ ) 으로 순회
• T 가 홀수이고, 대각선 칸의 개수가 짝수 ) 일 때는 아래 방향 ( ↙︎ ) 으로 순회

이 알고리즘을 풀기 전!

• 일단 T가 짝수일때, 홀수일때로 나눴다.(나누지 않고 하는 방법을 생각해내지 못했기 때문)

• T가 짝수일때 분자가 감소하고, 분모가 증가한다.

• 분자를 구하기 위해!

• 감소값(분자)을 나타내기 위해서는 아래와 같은 방법이 있다.
  1) 고정값 - 증가값
  2) 감소값 - 증가값
  3) 감소값 - 증가값

• 분모를 구하기 위해!

• 증가값(분모)을 나타내기 위해서는 아래와 같은 방법이 있다.
  1) 고정값 - 감소값
  2) 증가값 - 고정값
  3) 증가값 - 감소값

• 현재 알고있는 값은 X, T이고 / 알아낼 수 있는 값은 전 대각선의 칸 누적합, 현재 라인에 있는 대각선의 칸의 개수가 있다.

• 그 중 감소값은 분자말고 없고, 증가값 분모말고는 X값, 고정값은 직전 대각선의 칸의 누적합, 현재 라이에 있는 대각선의 칸의 개수, T가 있다. (실질적으로 전 대각선의 칸의 누적합과 현재 라인에 있는 대각선의 칸의 개수, T값은 증가하긴 하지만 현재 알고리즘을 T를 기준으로 나누기 때문에 고정값이 된다.)

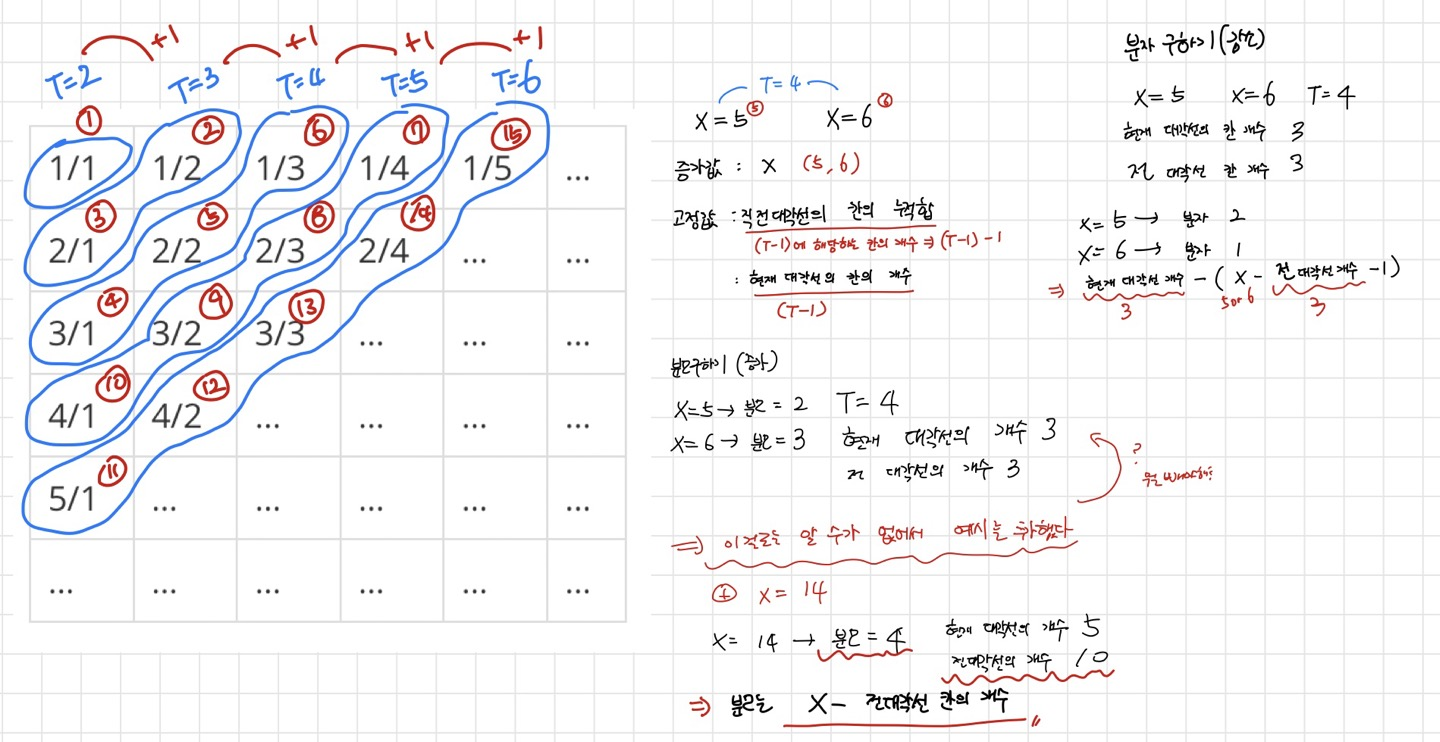
• 글씨가 알아보기 힘들 수 있지만, 해당 규칙으로 공식을 알아낸 것은 위의 사진과 같다.

/*T가 짝수일 때*/
//분자 (감소) => 고정값 - 증가값(= 증가값 - 고정값 - 고정값)
int 분자 = 현재대각선의_개수 - (입력받은_X - 전_대각선의_칸의_누적합_개수 -1);

//분모 (증가) => 증가값 - 고정값
int 분모 = 입력받은_X - 전_대각선의_칸의_누적합_개수;

• T가 홀수일때,분자가 증가하고, 분모가 감소한다.
  

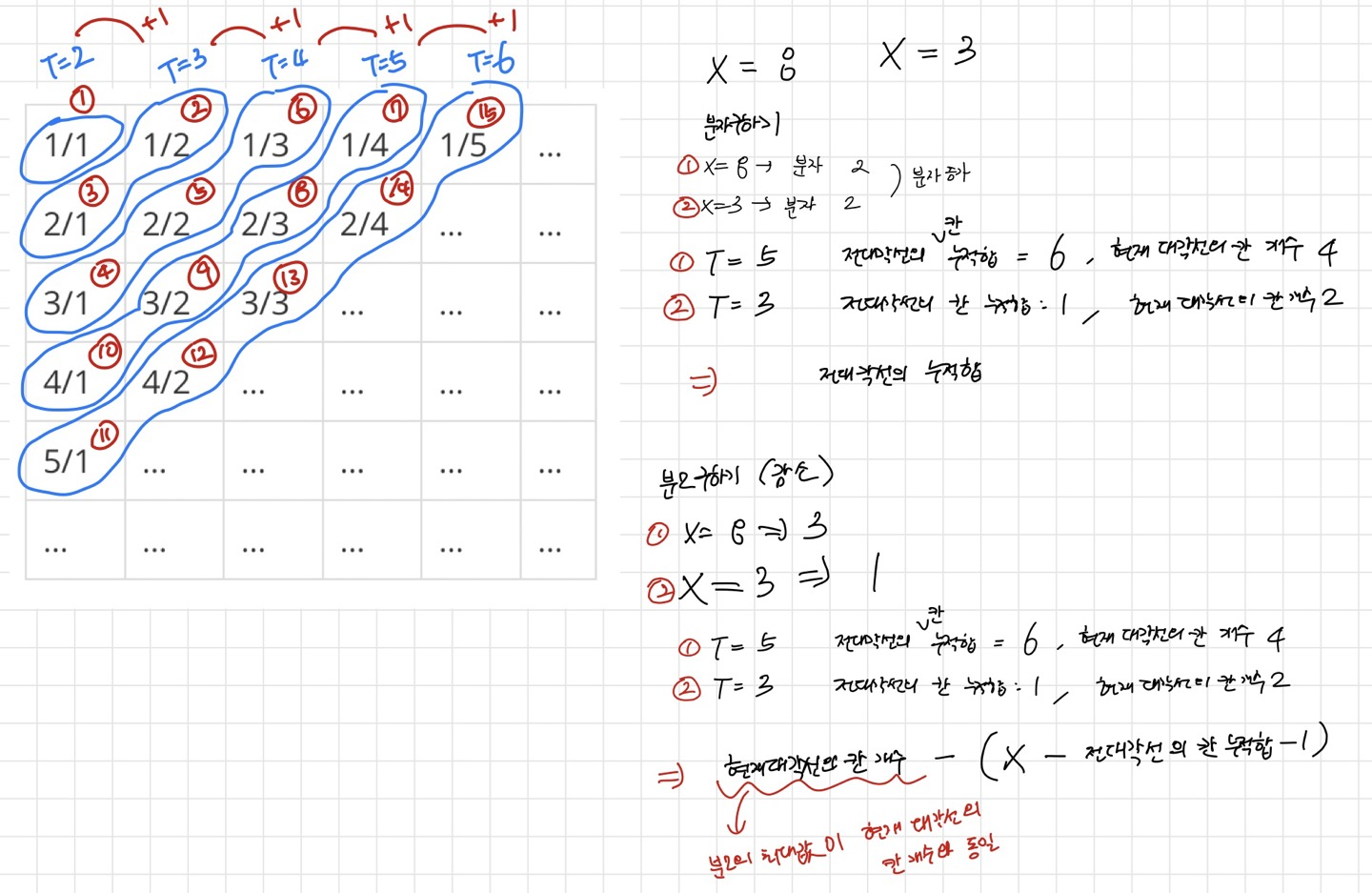
• T가 짝수일때랑 반대임으로 따로 설명할 것은 없다.

/*T가 홀수일 때*/
//분모 (감소) => 고정값 - 증가값(= 증가값 - 고정값 - 고정값)
int 분모 = 현재대각선의_개수 - (입력받은_X - 전_대각선의_칸의_누적합_개수 -1);

//분자 (증가) => 증가값 - 고정값
int 분자 = 입력받은_X - 전_대각선의_칸의_누적합_개수;

코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int X = Integer.parseInt(br.readLine()); //몇번째 분수인지.
        br.close();

        // 분수는 1/1부터 시작하는데, 해당 1/1의 대각선 라인에 칸의 개수는 1 => 초기값 1
        int squareCount = 1; // 해당 대각선(순회하는 대각선)에 있는 칸의 개수
        int squareSum =  0; // 해당 대각선의 전 대각선 칸을 누적 더하기 해서 저장하는 변수 (1/1보다 전은 없으니까 0)

        while(true){
            //  해당 대각선의 전 대각선 칸의 누적 칸 + 현재 해당하는 대각선의 칸의 개수보다 X번째가 작다는 것은
            // 현재 해당하는 대각선에 해당 X번째의 분수가 있다는 것!
            if(X <= squareSum + squareCount){
                if(squareCount % 2 == 1){ //해당 공식은 T와 같다. (해당 대각선의 칸 개수가 홀수, 분자+분모(T) = 짝수)
                    //대각선의 개수가 홀수인 범위 내에서는 위쪽(↗︎) 으로 순회 -> 분자 감소, 분모 증가
                    // ︎분자는 대각선에 있는 모든 칸의 개수 - (X - 해당 대각선의 전 대각선 칸누적 개수 -1)
                    System.out.println((squareCount-(X - squareSum -1) + "/" + (X - squareSum)));
                    break;
                }else{ //(해당 대각선의 칸의 개수가 짝수, 분자+분모(T) = 홀수)
                    //대각선의 개수가 짝수인 범위 내에서는 아래쪽(↙︎︎) 으로 순회 -> 분자 증가, 분모 감소
                    // ︎홀수와 반대로 계산하면 된다
                    System.out.println((X - squareSum) + "/" + (squareCount-(X - squareSum -1)));
                    break;
                }
            }else{ //아직 X번째 분수가 해당 대각선에 포함하지 않는 경우
                squareSum += squareCount;
                squareCount++; //대각선이 늘때마다 해당 칸의 개수도 +1늘기 때문에 +1
            }
        }

    }
}

• 코드의 설명은 주석으로 작성해놓았고, 자세한 설명은 위에 정리해놨기 때문에 코드설명은 따로 생략!

결과

느낀점

• 사실 이문제는 내 힘으로 푼 문제가 아니었다... 규칙은 찾았는데 코드 구현이 어려워서 정리되어있는 블로그에 가서 공부한 다음에 이해를 토대로 자세하게 설명을 했다.
• https://st-lab.tistory.com/74
  -> 참고한 블로그인데 정말 깔끔하게 설명되어있어서 이 문제 구현에 큰 도움이 되었다. (코드적으로는 이분이랑 똑같아서 거의 따라한 수준이긴하지만, 그래도 그걸 토대로 공부했고, 내 것으로 만들었다고 생각하기 때문에 보람있었다!)
  
• 언젠간은 이런 문제 참고하지 않고 내 힘으로 풀 수 있을 날이 오겠지...?