백준 1463 1로 만들기 [JAVA]

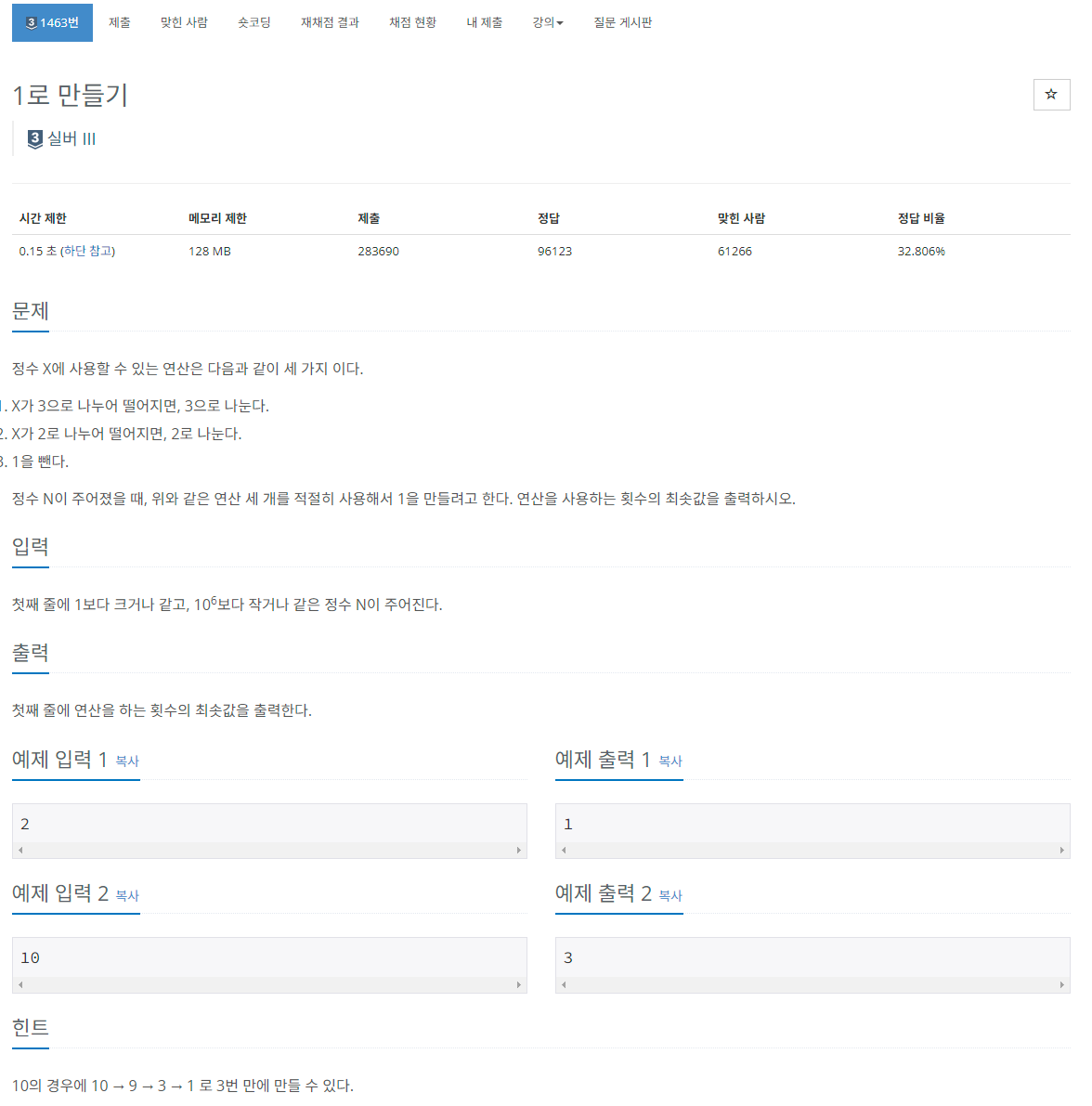
문제 해석

• 입력 받은 숫자(N)를 아래의 연산자를 통해 1을 만든다.
  1) X가 3으로 나누어 떨어지면, 3으로 나눈다.
  2) X가 2로 나누어 떨어지면, 2로 나눈다.
  3) 1을 뺀다.
• 단, 중요한 점은 1로 만드는 최소 횟수를 출력해야한다!.

입력 값 : 10

value = 10 dp[10] = ?
value%6 == 0 false
value%3 == 0 false
value%2 == 0 true
  dp[10] = Math.min(solution(value/2), solution(value-1))
  	> (solution(5), solution(9)) + 1

  	   > solution(5)
	     > value = 5 dp[5] = ?
	       > value%6 == 0 false
	       > value%3 == 0 false
	       > value%2 == 0 false
	       > value-1 => solution(4) + 1

		 > solution(4) 
		   > value = 4 dp[4] = ?
                     > value%6 == 0 false
		     > value%3 == 0 false
		     > value%2 == 0 true => (solution(2), solution(3)) + 1

			> solution(2) 
			  > value = 2 dp[2] = ?
			    > value%6 == 0 false
			    > value%3 == 0 false
		 	    > value%2 == 0 true => (solution(1), solution(1)) + 1
				> solution(1)
				  > *value = 1 dp[1] = ? = 0 not null

				> Math.min(solution(1), solution(1)) + 1 = Math.min(0, 0)+1 = 1
			 > *** solution(2) = 1

  			> solution(3)
			  > value = 3 dp[3] = ?
			    > value%6 == 0 false
			    > value%3 == 0 true => (solution(1), solution(2)) + 1
				> solution(1)
 				   > *value = 1 dp[1] = ? = 0 not null

			    > Math.min(solution(1), solution(2))+1 = Math.min(0, 1) + 1 = 1
			> *** solution(3) = 1 

		    > Math.min(solution(2), solution(3)) + 1 = Math.min(1, 1) + 1 = 2

		> *** solution(4) = 2

	      > *** solution(4) + 1 = 3

	     > *** solution(5) = 3

	     > value = 9 dp[9] = ?
	       > value%6 == 0 false
	       > value%3 == 0 true => (solution(3), solution(8)) + 1

		 > solution(3)
		   > value = 3 dp[3] = ? 
		    > 위의 과정 중 solution(3) 이미 진행 
		 => *** solution(3) = dp[3] = 1

		 > soltution(8)
		   > value = 8 dp[8] = ?
	  	    > value % 6 == 0 false
		    > value % 3 == 0 false
		    > value % 2 == 0 true => (solution(4), solution(7)) + 1

		      > solution(4)
			> 위의 과정 중 solution(4)는 이미 진행
		      => solution(4) = 2

		      > solution(7)
			> value = 7 dp[7] = ?
			  > value % 6 == 0 false
			  > value % 3 == 0 false
			  > value % 2 == 0 false
			  > value -1 => solution(6) + 1
			
			> solution(6)
		         > value = 6 dp[6] = ?
			   > value % 6 == 0 true => (solution(2), solution(3), solution(5)) + 1

			   > solution(2)
			     > 이전에 이미 solution(2) 진행 
                                           > *** solution(2) = 1
				
			   > solution(3)
			     > 이전에 이미 solution(3) 진행
			   > *** solution(3) = 1

			   > solution(5)
			     > 이전에 이미 solution(5) 진행
			    > *** solution(5) = 3

                                      > Math.min(solution(2), solution(3), solution(5)) + 1 => solution(1, 1, 3) + 1

		       > *** solution(6) = 2

		    > *** solution(7) = 3

                > Math.min(solution(4), solution(7)) + 1 => solution(2, 3) + 1 

              > *** solution(8) = 3

            > Math.min(solution(3), solution(8)) + 1 => solution(1, 3) + 1 
  	  
	  > *** solution(9) = 2

       > Math.min(solution(5), solution(9)) = solution(3, 2) + 1 
    
    > *** solution(10) = 3 => dp[10] = 3

		     

• 입력 값이 10일 경우를 예시로 들어 진행을 해보았다.
• 그렇게 되니 끝에 +1을 더하는 것은 연산을 진행하는 횟수와 같다. (얼마나 더 깊이 들어가는지 확인할 수 있음...)

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;

public class Main {

    static Integer[] dp;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

         dp = new Integer[N+1];

         dp[0] = dp[1] = 0; //dp[0]의 값은 쓰지 않는다.

        System.out.println(solution(N));

    }

    //최소 횟수를 구하는 솔루션 함수
    public static int solution(int value){
        if(dp[value] == null){
            // 여기서 중요한 점은 무조건 큰 수로 나눈다고 적은 횟수가 아님!
            // => 즉, 각 연산 별 최소값을 구해야 함!
            if(value % 6 == 0) { //2, 3 나누는 거 다 되고 -1도 됨(-1은 안되는 경우가 없음)
                dp[value] = Math.min(Math.min(solution(value/3), solution(value/2)), solution(value-1))+1;

            }else if(value % 3 == 0){ //나누기 3과 -1만 되는 경우
                dp[value] = Math.min(solution(value/3), solution(value-1))+1;

            }else if(value % 2 == 0){ //나누기 1과 -1만 되는 경우
                dp[value] = Math.min(solution(value/2), solution(value-1))+1;

            }else{ //-1만 되는 경우
                dp[value] = solution(value-1)+1;
            }
        }

        return dp[value];
    }
}

결과

느낀 점

• 처음에 무조건 큰 숫자 순서대로 나누면 최소 횟수가 나올거라고 생각했다가 예시처럼 출력이 안돼서 좀 헤맸었지만 그래도 어찌저찌 풀었다.