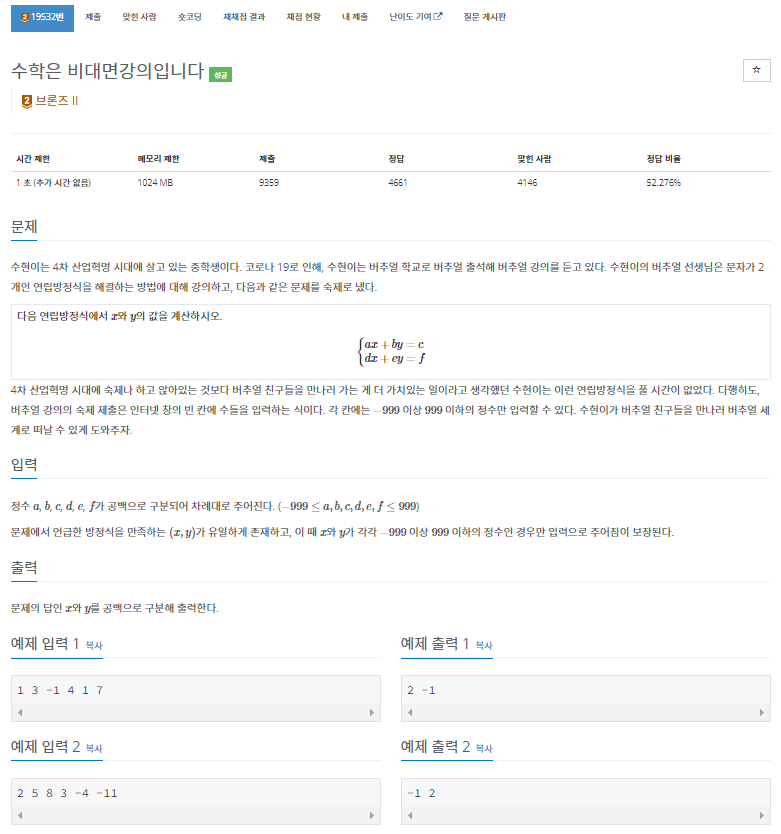
문제 풀이
- 문제는 간단한 연립방정식문제이다.
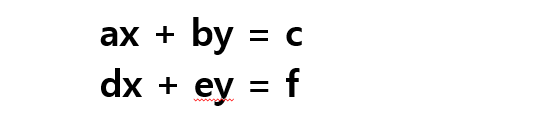
- a, b, c, d, e, f 순으로 입력받아, 해당 x와 y의 값이 무엇인지 찾으면 되는 문제이다.
- x와 y는 -999이상 999이하이므로 해당 범위만큼 반복하여 대입하여 풀면 된다.
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
br.close();
//첫번째 식
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
// 두번째 식
int d = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int f = Integer.parseInt(st.nextToken());
//각각의 x, y가 -999 <= x, y <= 999이기 때문에
for(int i = -999; i <= 999; i++) {
for(int j = -999; j <= 999; j++) {
if(a*i + b*j == c){ // ax + by 가 C이고(x = i, y = j)
if(d*i + e*j == f) { // dx + ey가 f일 때(x = i, y = j)
bw.write(i + " " + j + "\n");
break;
}
}
}
}
bw.flush();
bw.close();
}
}결과

-
-999 ~ 999 까지의 범위를 해를 찾을 때까지 반복하다보니까, 시간이 너무 많이 걸리는 것을 볼 수 있다.
-
그래서, 다른 분의 코드를 찾아봤는데, 연립방정식을 풀때 쓰는 공식인 가감법을 사용하여 소요 시간을 줄일 수 있다고 설명되었다.
-
가감법은 수학으로 풀 수는 있지만, 코드로 칠때는 솔직히 이해가 되지 않는다.

-
가감식으로 풀때의 공식은 아래와 같다고 한다.
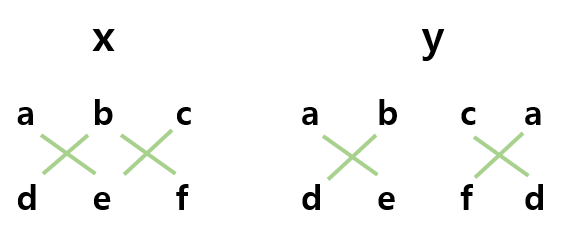
-
사실 이 공식이 어떻게 나왔는지는 아직 이해하진 못했다.
코드2
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
br.close();
//첫번째 식
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
// 두번째 식
int d = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int f = Integer.parseInt(st.nextToken());
bw.write((c*e- b*f) / (a*e - b*d) + " "); //x축
bw.write((c*d - a*f) / (b*d - a*e) +""); // y축
bw.flush();
bw.close();
}
}- 가감법을 사용한 코드는 위의 코드와 같다.
결과2

- 훨씬 빠르다....
느낀점
- 요즘 느끼는 건 코드를 짤 때 무엇이 최적인지 구분을 못하는 것과 수학적으로 푸는 게 많이 부족하다는 것을 깨닫고 있다.(문해력도...)
- 그 감을 잡기 위해서는 뭘 해야할지도 아직 감이 잡히지 않지만... 수학식을 코드로 녹여내는 그런 스킬도 많이 배워야겠다고 생각이 들었다. (전혀 이 문제에서 먼저 가감법을 생각해내지 못했다.) => 물론,, 가감법 공식 계속 보고 있는데 어떻게 하면 그 공식이 나오는지 이해도 되지 않는다...


가감법 공식
첫번째 방정식 양변에 d를 곱함, 두번째 방정식 양변에 a를 곱함
위에서 나온 두 식을 가감