백준 24060 알고리즘 수업 - 병합 정렬 1 [JAVA]

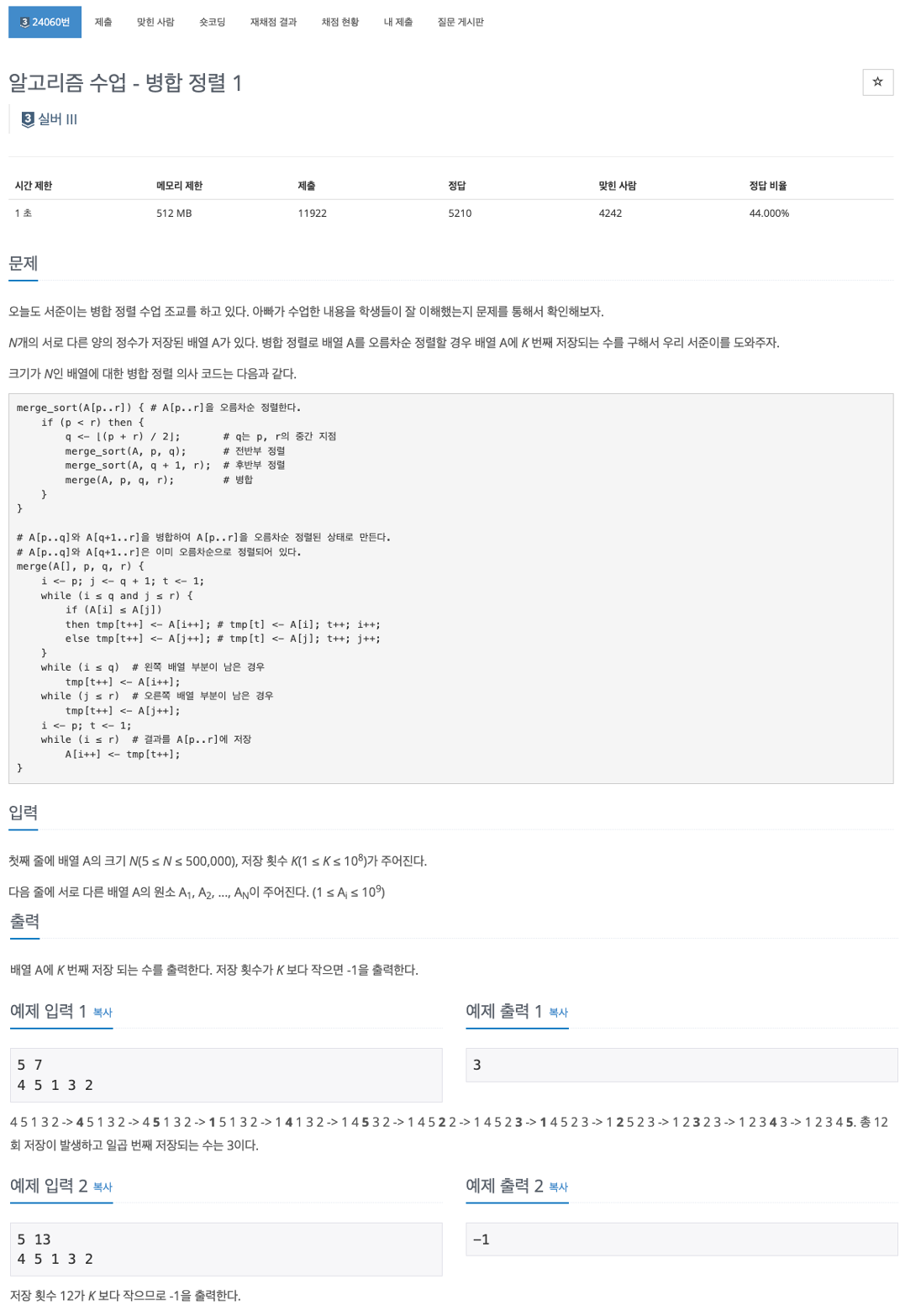
문제 해석

• 문제는 제목 그대로 병합 정렬을 하여 오름차순으로 정렬하는 것이다.
• 그렇다면, 병합 정렬(= 합병 정렬, merge sort)은 무엇일까?
• 분할(Divide) : 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
• 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
• 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다
  
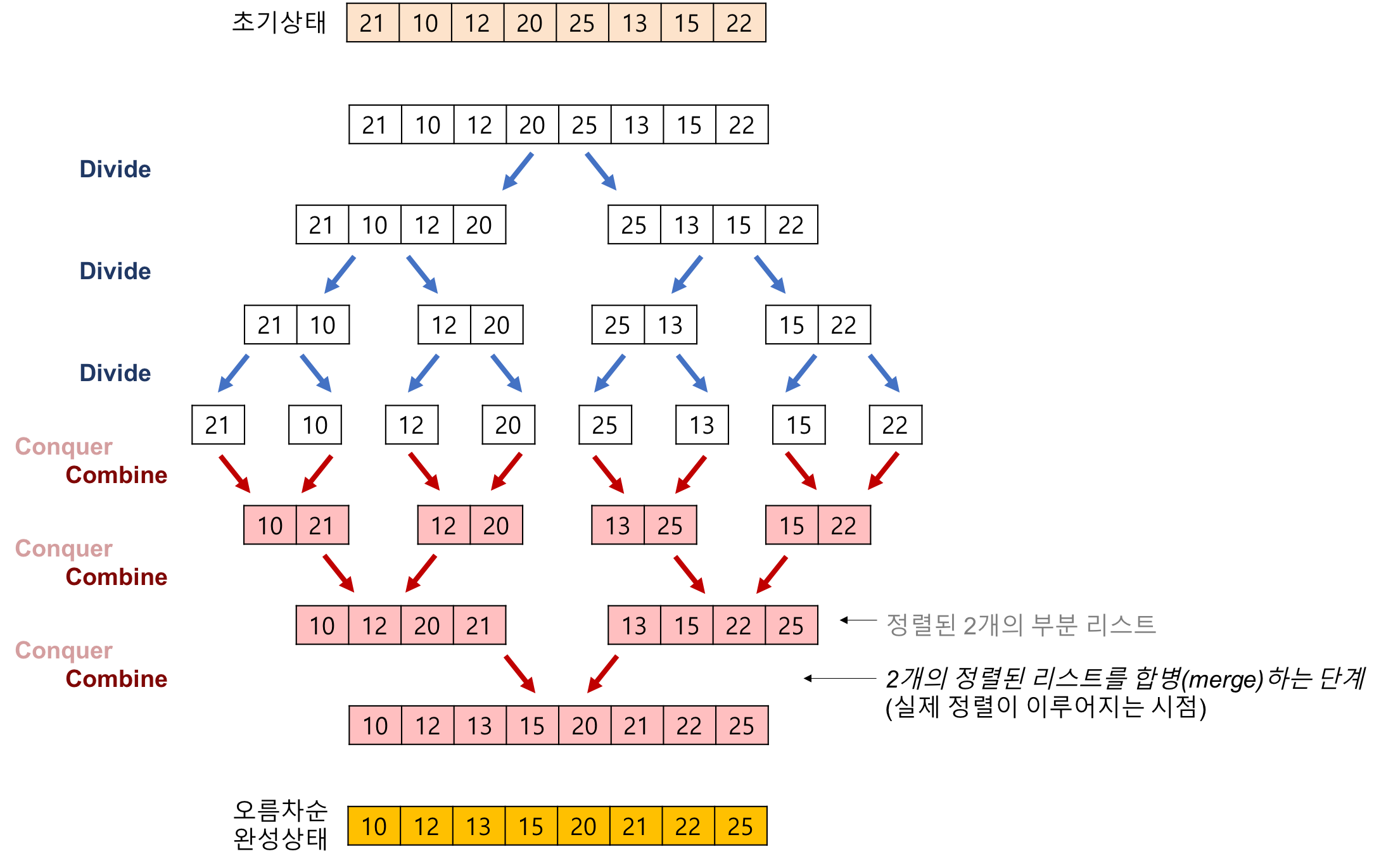
  출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
• 다시 문제로 넘어오면, 첫번째 줄에서 배열의 크기(N)과 저장 횟수(K)를 입력받는다.
• 입력받았다면 N개만큼 배열의 원소를 입력받는다.

코드

import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    int[] A; //입력받은 배열
    static int[] tmp; //정렬 후 저장하는 배열
    static int result = -1; //결과 저장 (실패시 -1)
    static int cnt = 0; //저장 횟수 누적 저장
    static int K; // 저장 횟수

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken()); // 배열의 크기
        K = Integer.parseInt(st.nextToken()); // 저장 횟수

        int[] A = new int[N];
        tmp = new int[N]; //오름차순 정렬해서 저장할 배열 초기화

        st = new StringTokenizer(br.readLine());

        for(int i = 0; i < N; i++){ //배열의 요소 입력 받기
            A[i] = Integer.parseInt(st.nextToken());
        }

        merge_sort(A, 0, N-1); //처음 시작점 0, 마지막 인덱스 : N-1(배열은 0부터 시작하기 때문)

        System.out.println(result);
    }

    //오름차순 정렬하는 메소드
    static void merge_sort(int A[], int p, int r){
        if(cnt > K) return; //저장 횟수가 진행 횟수보다 넘어가게 되면 더이상 분해 or 병합 진행X
        if(p < r){
            int q = (p+r)/2; //중간으로 쪼갠다.
            merge_sort(A, p, q);   //전반부 정렬
            merge_sort(A,q+1, r); //후반부 정렬
            merge(A, p, q, r); //병합
        }
    }

    //병합하는 메소드
    /*
     [파라미터]
     p : 시작 점 (인덱스)
     q : 중간 점 (인덱스) _ 쪼갠 배열의 첫번재 배열
     r : 마지막 점 (인덱스)
    */
    static void merge(int Array[], int p, int q, int r){
        int i = p;
        int j = q + 1; //쪼갠 배열(2번째) 시작 인덱스
        int t = 0;

        //시작 인덱스가 중간 인덱스(1번쨰)보다 작고,
        //중간인덱스(2번째)가 마지막인덱스보다 작을 경우 반복
        while(i <= q && j <= r){
            if(Array[i] < Array[j]){ //만약 Array[i](=앞의 값)이/가 Array[j](=뒤의 값)보다 작을 경우
                tmp[t++] = Array[i++]; //작은 값을 넣어주고
            }
            else{//만약 Array[i](=앞의 값)이/가 Array[j](=뒤의 값)보다 크거나 같을 경우
                tmp[t++] = Array[j++]; //작은 값이 Array[j]이므로 작은 값을 차근차근 쌓는다.
            }
        }

        //다 정렬하고도 남은 경우
        while(i <= q){ //왼쪽 배열이 남은 경우
            tmp[t++] = Array[i++]; //tmp배열에 저장하는 정수
        }

        while(j <= r){ //오른쪽 배열이 남은 경우
            tmp[t++] = Array[j++]; //tmp배열에 저장하는 정수
        }

        i = p;
        t = 0;
        while(i <= r){ //결과를 배열 A에 저장한다. i(시작), r(끝)
            cnt++;

            if(cnt == K){ //저장횟수가 같다면
                result = tmp[t]; //해당 증가한 만큼의 t인덱스의 값을 result변수에 담고
               break;
            }

            Array[i++] = tmp[t++]; //A에 순서대로 정렬된 값을 저장
        }
    }
}
        

• 콘솔에 찍힌 결과.(수행 절차)
  

 /* 
  	예를 들어, 입력 값이 아래의 정수이라고 가정할 때,
  	5 7
	4 5 1 3 2 
*/
  
Array 배열 (2) : 4 5 1 3 2 
tmp 배열 (2): 4 5 0 0 0 
Array 배열 (2) : 4 5 1 3 2 
tmp 배열 (2): 4 5 0 0 0 
Array 배열 (2) : 1 5 1 3 2 
tmp 배열 (2): 1 4 5 0 0 
Array 배열 (2) : 1 4 1 3 2 
tmp 배열 (2): 1 4 5 0 0 
Array 배열 (2) : 1 4 5 3 2 
tmp 배열 (2): 1 4 5 0 0 
Array 배열 (2) : 1 4 5 2 2 
tmp 배열 (2): 2 3 5 0 0 
Array 배열 : 1 4 5 2 2  -> 정렬을 하다가 cnt = K를 만나 종료되는 것을 알 수 있다. (즉, 정렬이 되다 끝남...)
tmp 배열 : 2 3 5 0 0 
- 이 아래부터는 재귀함수를 썼기 때문에 merge_sort에서 if(cnt > K) return 안걸린 부분을 수행하는 것을 알 수 있다.
Array 배열 (2) : 1 4 5 2 2
tmp 배열 (2): 1 2 2 4 5 
Array 배열 (2) : 1 2 5 2 2 
tmp 배열 (2): 1 2 2 4 5 
Array 배열 (2) : 1 2 2 2 2 
tmp 배열 (2): 1 2 2 4 5 
Array 배열 (2) : 1 2 2 4 2 
tmp 배열 (2): 1 2 2 4 5 
Array 배열 (2) : 1 2 2 4 5 
tmp 배열 (2): 1 2 2 4 5   
- merge_sort에서 if(cnt > K) return에 걸려 분리와 정렬은 완전히 끝이 난다.

결과

느낀 점

• 의사코드를 보고 코드로 그대로 옮기면 금방 풀 수 있었겠지만 그냥 가져다 쓰기보단 로직을 이해하고 싶었다...
• 그 덕분에 이 로직을 이해하는데 3일 연속으로 보고 또 봤고... 생각보다 너무 오래걸렸다. (머리가 많이 굳었긴 했나보다... 꾸준히 해야하는데😩)