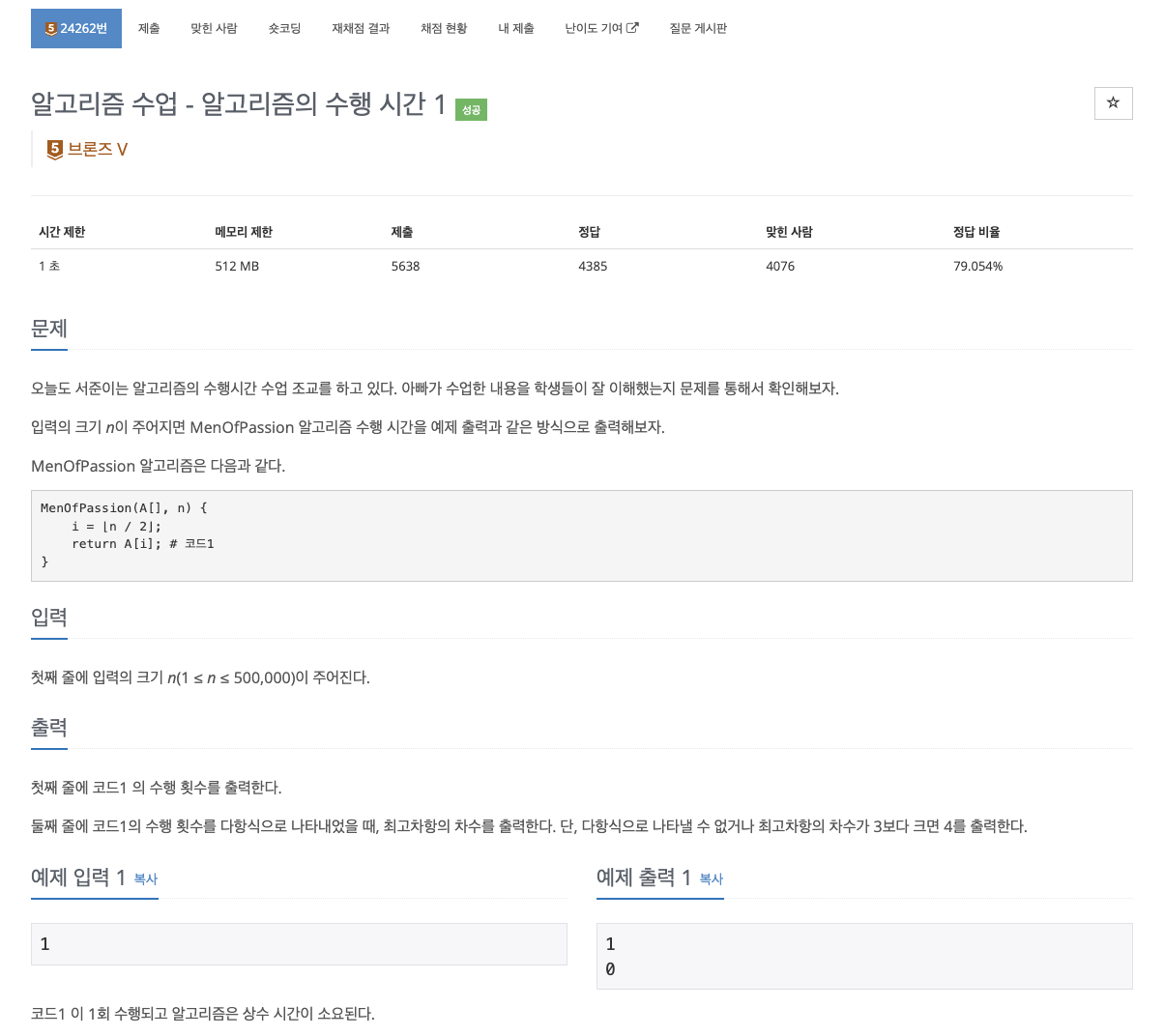
문제 해석
- 이 문제의 코드 어처구니 없이 심플 그 자체인데, 사실 문제를 이해하는 것이 어려웠다.
- 말이 어렵게 느껴지는 건 기분 탓일까...?
- 암튼 문제 해석을 해보자면, 콘솔로부터 입력 크기 n을 입력받아 해당 위의 알고리즘의 수행횟수와 알고리즘 수행 시간을 예제로 출력하면 되는 문제이다.
이 문제를 이해하기 위해선 위의 코드를 분석해야 한다.
- 일단, 코드를 살펴보면
//MenOfPassion 알고리즘
MenOfPassion(A[], n) { //n이 입력받은 입력 크기이고
i = ⌊n / 2⌋; // 입력 크기를 반을 나눈 것은 i변수에 저장한 후
return A[i]; # 코드1 // A[i] 번째의 값을 반환한다.
}- 코드를 보면 딱 한번 실행되는 것을 알 수 있다. (그 이유 : 반복문이 없고 반환하기 때문에!)
- 그렇기 때문에 어떤 수가 들어와도 딱 1번 수행되는 것을 알 수 있다.
-> 주어진 코드만 봤을 때! - 그 다음은 수행 시간을 알면되는데, 밑에 설명에 보면,
둘째 줄에 코드1의 수행 횟수를 다항식으로 나타내었을 때, 최고차항의 차수를 출력한다. 단, 다항식으로 나타낼 수 없거나 최고차항의 차수가 3보다 크면 4를 출력한다.
- 나는 이 문장이 빅오표기법의 시간 복잡도로 표현하라 라고 이해했다.
- 그래서, 맞게 이해한건지는 모르겠지만, 일단 수행은 1번만되기 때문에 수행시간은 O(1)로 상수 시간이 걸린다! => 쉽게 풀어서 말하면 위의 코드를 수행하는 데 오직 한 단계만 처리하는 것을 의미한다.
빅오 표기법_시간 복잡도
O(1) – 상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
*O(log n)** – 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
O(n) – 직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
O(n log n) : 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼의 수행시간을 가진다. (선형로그형)
O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
O(C^n) – 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱.
-
정말 깔끔하게 정리하신 분의 블로그(덕분에 다시 공부했다.)
-
너무 돌아왔지만, 다시 말해 둘째 줄에 출력하는데, 최고차항의 차수는 빅오표기법의 시간 복잡도의 제곱승을 의미한다.
만약, 해당 시간복잡도 식이 n^5 + 2n^3 + 10; 이 나왔다고 가정했을 때
빅오표기법의 시간복잡도롤 나타내면 O(n^5)이다.
=> 빅오표기법의 시간복잡도의 계산자체가 최고차항의 차수만 남기고 버리니까(?) 아마 이걸 말하는게 아닌가? 싶다!
=> 다시 문제로 돌아가면,> 다항식으로 나타낼 수 없거나 최고차항의 차수가 3보다 크면 4를 출력한다.- 위 문장은 해당 시간 복잡도를 위와 같은 식으로 나타내지 모하거나 최고차항 차수가 3보다 크면 그냥 다 4로 출력해라라는 것!
=> n^5 + 2n^3 + 10 을 이 24262번 문제에 적용하면 4가 나와야한다.
- 위 문장은 해당 시간 복잡도를 위와 같은 식으로 나타내지 모하거나 최고차항 차수가 3보다 크면 그냥 다 4로 출력해라라는 것!
-
설명이 너무 길어졌지만, 사실 이 문제는 이렇게 장황하게 설명할 필요가 없다.
-
이미 답은 나왔기 때문!
-
위에 설명한 바와 같이 이 24262번 문제는 어떤 숫자를 입력해도 수행횟수가 1번이고, 수행시간은 O(1)이다.
-
그냥, 1과 0을 줄바꿈해서 출력하면 됨....
코드
public class Main {
public static void main(String[] args) {
//어떤 수가 들어와도 값은 똑같기 때문에 입력받지 않아도 됨
System.out.println(1);
System.out.println(0);
}
}결과

느낀점
- 이 문제 덕분에 빅오표기법에 대해 다시 공부할 수 있는 기회가 되었다.
- 문제 코드가 이렇게 간단한건 "Hello World!" 문제 이후로는 처음인 것 같아서 신선했다!
