백준 24265 알고리즘 수업 - 알고리즘 수행 시간4 [JAVA]

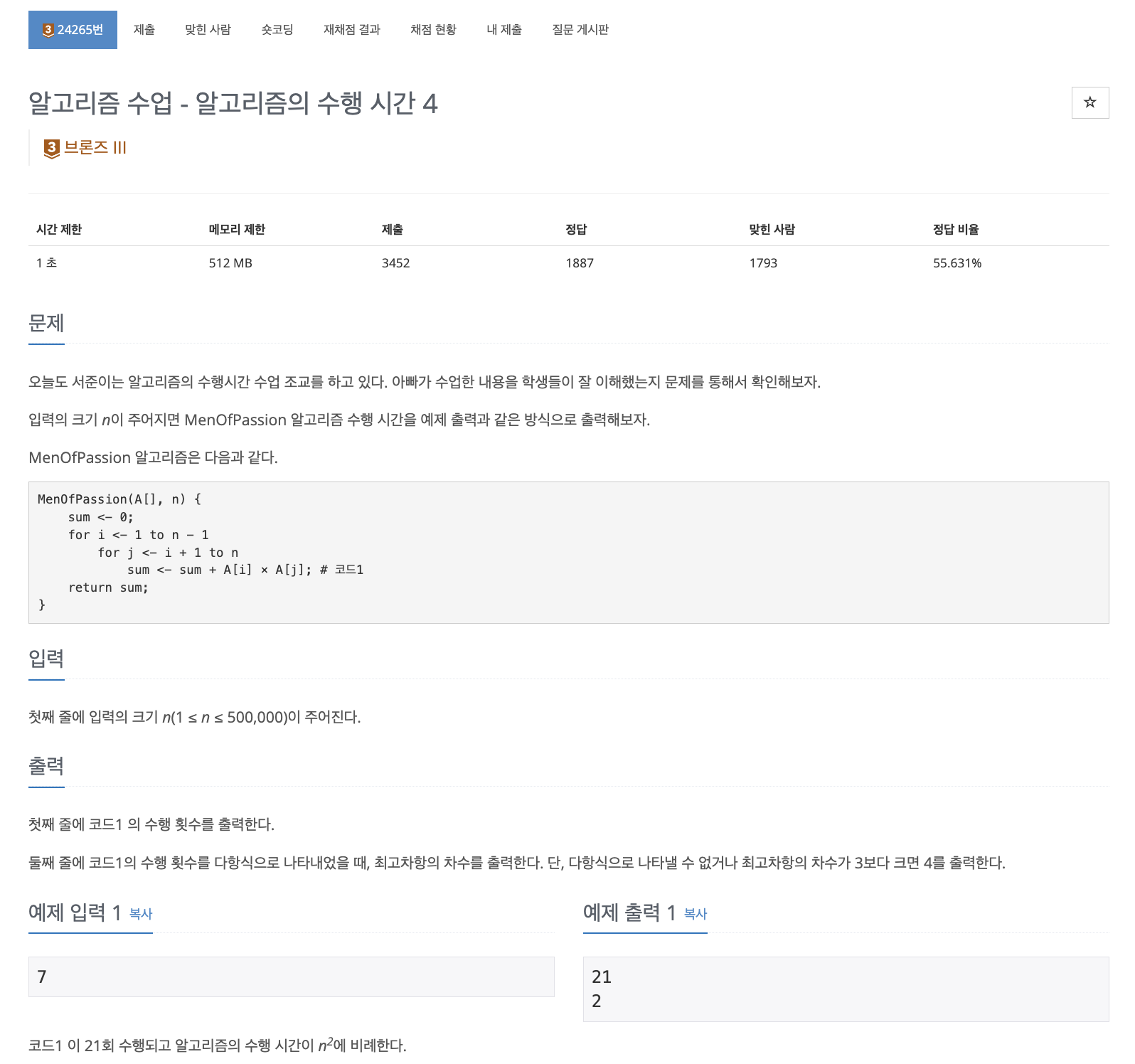
문제 해석

• 이번 포스트 또한 전 포스트의 연장선이 되는 문제이다.

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n - 1
        for j <- i + 1 to n
            sum <- sum + A[i] × A[j]; # 코드1
    return sum;
}

• 주어진 코드는 위의 코드와 같은데, 사실 조금 불편하다. (그래서 익숙한 언어인 자바로 바꿔보았다. 수행 횟수를 출력하는 코드로)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());

        int count = 0; //수행 횟수를 저장하는 변수

        for(int i = 1; i <= n-1; i++){
            for(int j = i+1;  j <= n; j++){
                count++;
            }
        }

        System.out.println(count);

    }
}

• 해당 코드는 반복문이 한번 돌때마다 카운트를 해서 입력받은 숫자를 기준으로 수행하는 횟수를 출력하는 코드인데, 수행 횟수에 규칙성이 보인다!
• 이해하기 쉽게 7로 가정해보자.

  n = 7
  i는 1부터 n-1으로, 즉 1~6만큼 돈다.
  j는 i+1부터 n까지 반복문을 도는데, j 반복문은 i 반복문 내부에 있으므로 i가 1번 돌때 j는 i+1 ~ n만큼 도는 것을 알 수 있다.

  		i = 1         j = 2 ~ 7 [2, 3, 4, 5, 6, 7] => 6번
  		i = 2		  j = 3 ~ 7 [3, 4, 5, 6, 7] => 5번
          i = 3 		  j = 4 ~ 7 [4, 5, 6, 7] => 4번
          i = 4		  j = 5 ~ 7 [5, 6, 7] => 3번
          i = 5 		  j = 6 ~ 7 [6, 7] => 2번
          i = 6		  j = 7		[7] => 1번

  • 1 ~ 6까지 더한 값이 수행 횟수이다.
  • 이 공식은 익히 알고 있을텐데 1 ~ n까지 합을 구하는 공식은 n(n+1)/2의 공식을 사용하면 된다!
  • 그렇다면 6은 어떻게 나온 것일까?
  • 바로 i의 마지막 반복번호(?)이다.
  • 즉, n-1값이고 그것을 공식에 대입하면, (n-1)((n-1)+1)/2 = n(n-1)/2이다

정리

• 수행 횟수 : n(n-1)/2
• 시간 복잡도(=최고차항) : O((n^2 - n)/2) => 최고차항빼고 다 무시하면 O(n^2) 이다.

코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(br.readLine());
        br.close();

        bw.write(n*(n-1)/2 + "\n" + 2);
        bw.flush();
        bw.close();
    }
}

결과

느낀점

• 고등 수업 과정이였던 등차수열의 합공식이 나왔는데, 진짜 기억이 가물가물했다... 지겹도록 했던 것인데도 말끔하게 까먹고 있었다는게 엄청난 충격이고 코딩공부도 고등 수학처럼 되지않도록 진짜 꾸준히 해야겠다 싶었다.