백준 24267 알고리즘 수업 - 알고리즘 수행 시간6 [JAVA]

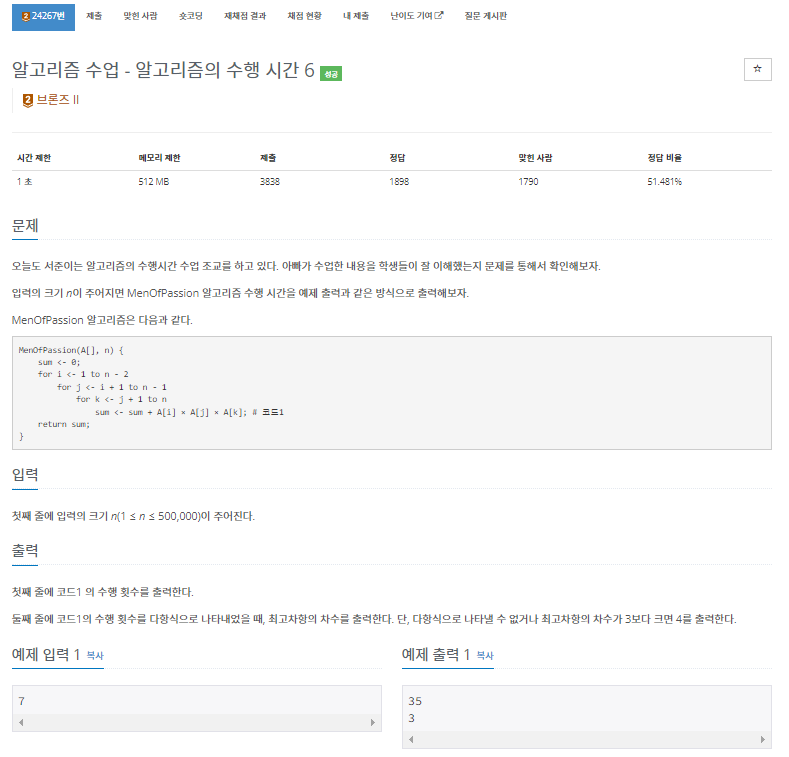
문제 해석

• 이번 포스트 또한 <알고리즘 수업 - 알고리즘 수행 시간1~5>의 연장선인 내용이다.
• MenOfPassion 알고리즘을 JAVA 코드로 바꾸면 아래와 같다.

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        long n = Long.parseLong(br.readLine());

        int count = 0;

        for(int i = 1; i <= n-2; i++){
            for(int j = i+1; j <= n-1; j++){
                for(int k = j+1; k <= n; k++){
                    count++;
                }
            }
        }

        br.close();

        bw.write(count+"\n" + 3);
        bw.flush();
        bw.close();

    }
}

• 이 코드를 제출해도 정답이긴 하겠지만, 시간 단축을 위해 알고리즘 규칙을 찾아 코드를 작성할 예정이다.

n이 7이라고 가정했을 때,
i는 1부터 5까지 반복,
j는 i+1 부터 6까지 반복,
k는 j+1 부터 7까지 반복,

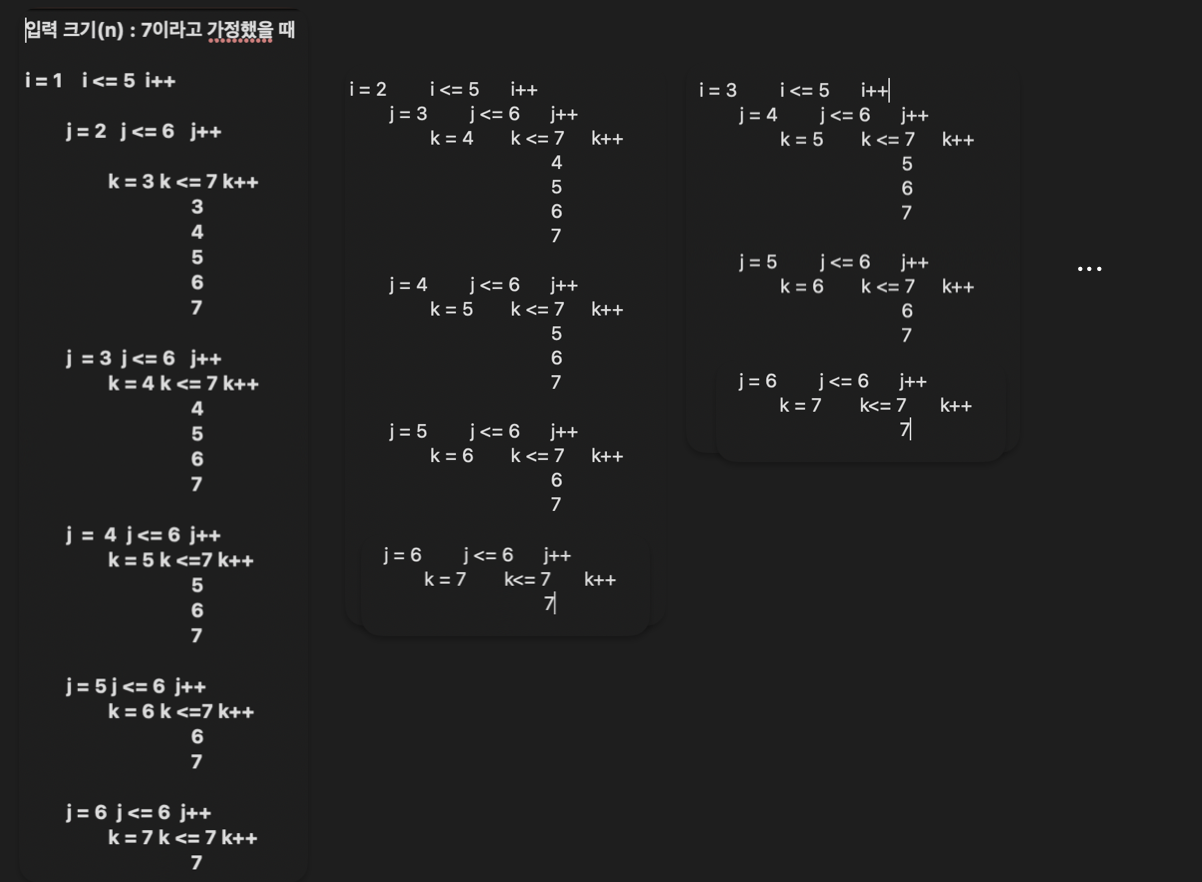
• 이런식으로 수행하고, 수행 횟수는 i를 기준으로, 15, 10, 6, 3, 1으로 점점 감소한다.
• -5, -4, -3, -2으로 줄어든다라는 규칙성은 찾았지만, 식으로 바꿀 수 없었다.
• 그래서, 다른 분의 해석을 참고하였다.

  • 1 부터 n까지의 숫자중 3가지(i, j, k에서 하나씩 뽑는거라 볼 수 있음)를 뽑아 중복 없이, 크기 순으로 작성하는 경우의 수가 수행 횟수이다.

  • 즉, 이 공식은 고등과정 학률과 통계-조합부분에 해당되는데,
    

  • 이 공식을 사용하면,
    

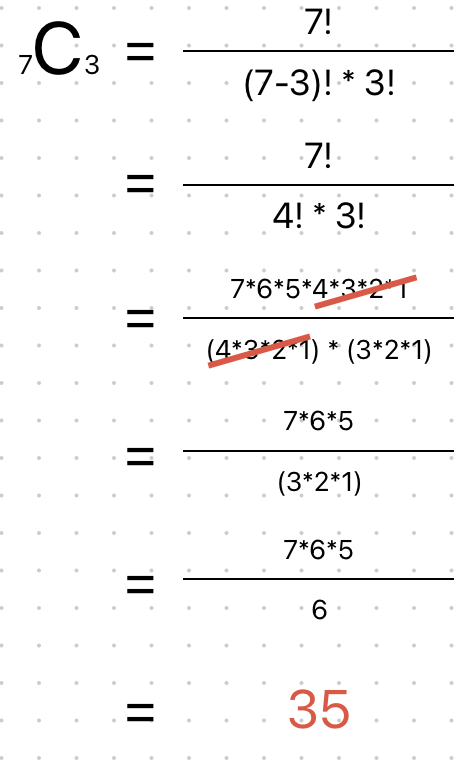
  • 즉 수행 횟수는 35이고, 공식을 정리하면, 아래와 같다.

    

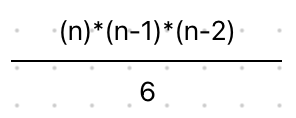
  • 시간 복잡도는 O(n X (n-1) X (n-2)/6)의 최고차항 차수인 3이 된다.

코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        long n = Long.parseLong(br.readLine());

        br.close();

        bw.write((n*(n-1)*(n-2)/6)+"\n" + 3);
        bw.flush();
        bw.close();

    }
}

결과

느낀점

• 고등 수학 다 까먹어서 수학을 다시 공부해야하나...싶다.