백준 2485 가로수 [JAVA]

Ga0·2023년 5월 23일

Java beakjoon 백준 자바

baekjoon

목록 보기

54/137

문제 해석

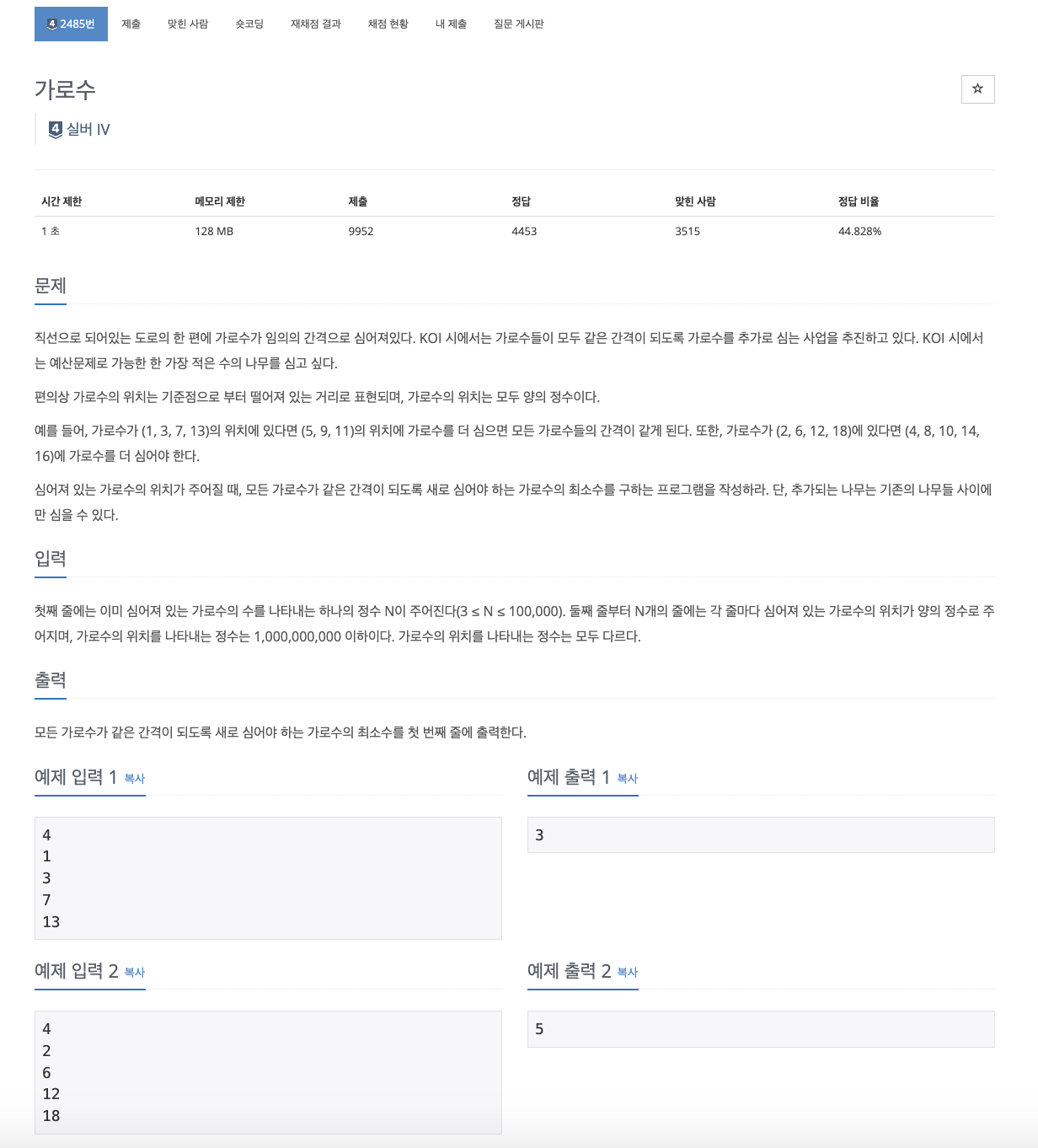
가로수의 개수(N)을 입력받고, 가로수의 개수만큼 가로수의 좌표(위치)값을 입력받는다.
현재 심어진 가로수의 좌표(위치)값을 모두 입력받았다면, 그 값들을 가지고 가로수와 가로수 사이의 간격이 모두 동일하도록 가로수를 추가하여, 최소로 추가할 수 있는 가로수의 개수를 구하면 된다.
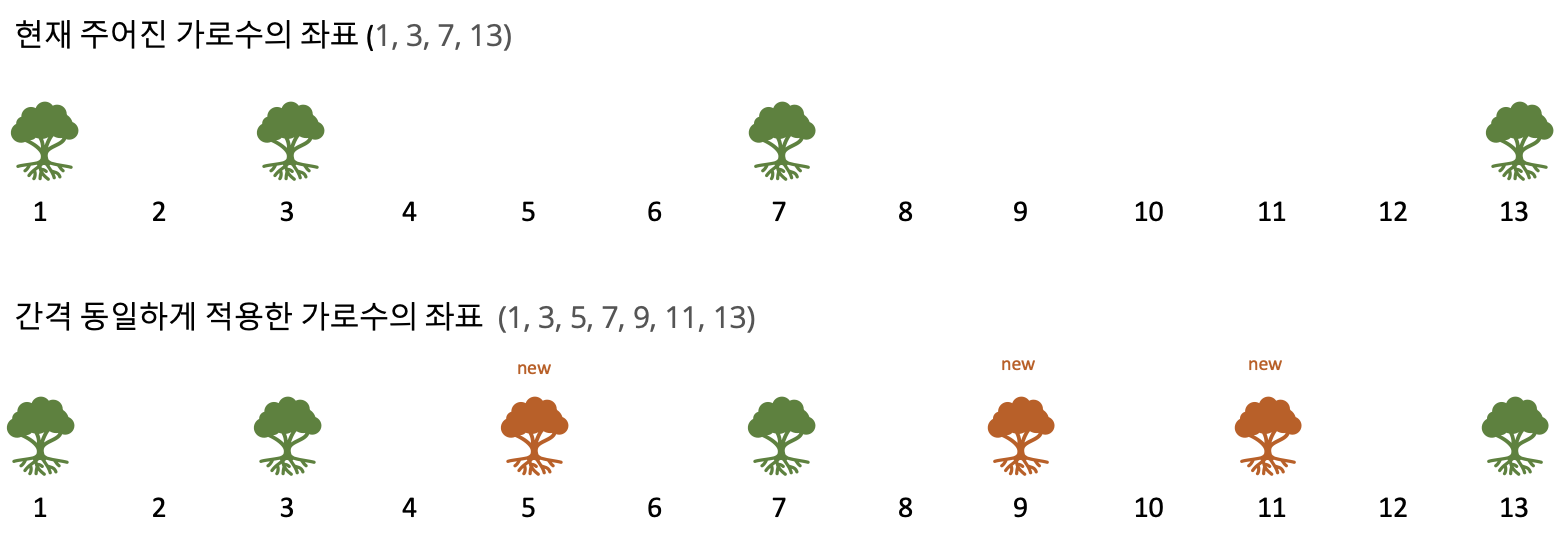
이런 식으로 간격을 동일하게 가로수의 나무를 심고, 새로 심은 나무의 개수를 반환하면된다. (위의 예시로는 3이 된다.)

어려웠던 점

최대 공약수로 풀어야하는 문제인데, 계산을 해서 풀려고 했다. 그래서 어려움이 존재했는데,,,
간격들의 최대 공약수를 구해야하는 이유는 간격이 일정하면서 간격은 최대한 커야 된다 라는 조건이 있기 때문이다.
단순하게 생각했을 때에는 거리를 구해서 간격의 최대공약수를 구하게 되면, 거리마다 최대 공약수가 갱신되니 최대니까
이러한 경우 최대 간격이 7 ~ 13인 6이 되는데 1 ~ 3인 경우와 3 ~ 7인 경우는 그 간격을 가질 수 없으니 문제되는게 아닌가? 싶었지만, 너무 단순하게 생각하는 바람에 생긴 오해였다.
아래 코드를 보면 gcd값이 보일 것 이다. 즉 gcd는 가로수의 간격들의 최대 공약수를 정하는 변수인데, 실질적으로 보면 가로수의 좌표(위치)의 최대 공약수를 구하는게 아니라 가로수의 간격의 또 다른 가로수의 최대 공약수 값의 최대 공약수를 구하는 것이다.

        int gcd = 0; //가로수 간격의 최대 공약수를 저장하는 변수

        for(int i = 0; i < N-1; i++){
            int distance = streetTree[i+1] - streetTree[i];
            gcd = findGCD(distance, gcd); //가로수 간격의 최대 공약수
        }

말이 어려운데 그림으로 설명하면, 아래와 같다.
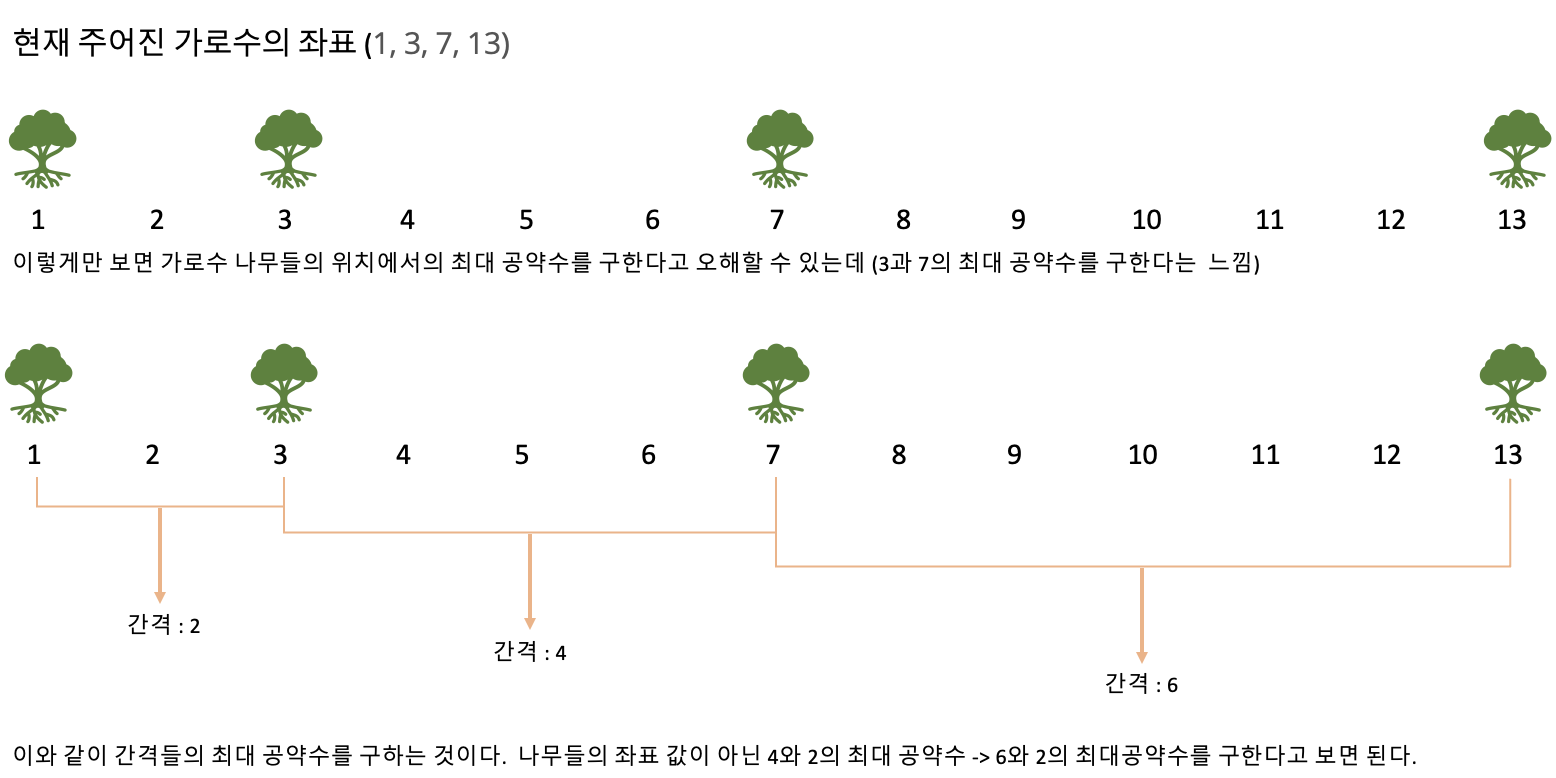
코드에서 볼 수 있듯이 처음은 2와 0(0은 모든 수의 최대 공약수이다.)의 최대 공약수를 구하고 그걸 gcd1이라고 하면 다음은 4, 2의 최대 공약수를 구하는 것이 아니라 4와 gcd1의 최대 공약수를 구한다.
이를 통해, 2와 0의 최대 공약수와의 최대 공약수를 구하기 때문에 2와의 최대공약수도 보장받을 수 있다. (=> 유클리드 호제법 공식에 의하면)
위와 같은 증명을 통해 최대공약수를 보장받는 것을 확인할 수 있다.

코드

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main {
    public static void main(String[] args) throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());

        int[] streetTree =new int[N];

        for(int i = 0; i < N; i++){
            streetTree[i]=Integer.parseInt(br.readLine());
        }

        br.close();

        int gcd = 0; //가로수 간격의 최대 공약수를 저장하는 변수

        for(int i = 0; i < N-1; i++){
            int distance = streetTree[i+1] - streetTree[i];
            gcd = findGCD(distance, gcd); //가로수 간격의 최대 공약수
        }

		//(streetTree[N-1]-streetTree[0])/gcd은 간격의 수니까
        //가로수의 나무의 개수를 구하려면 간격의 수에서 + 1을 해야한다. 
        bw.write((streetTree[N-1]-streetTree[0])/gcd+1-(streetTree.length) + "");
        bw.flush();
        bw.close();

    }

    //최대 공약수 구하기
    static int findGCD(int A, int B){
        while(B != 0){
            int R = A%B;
            A = B;
            B = R;
        }
        return A;
    }
}