백준 25682 체스판 다시 칠하기2 [JAVA]

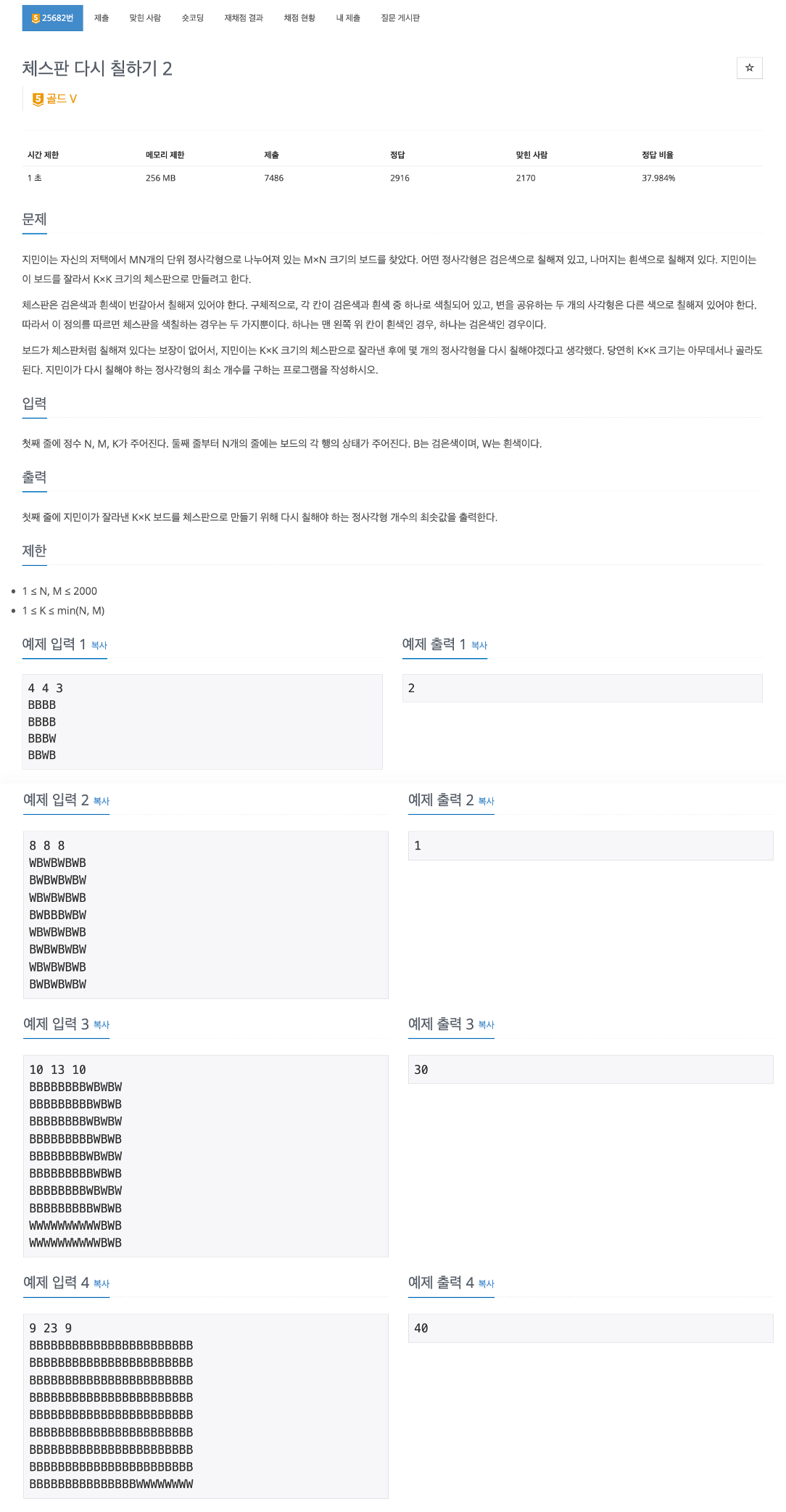
문제 해석

• 첫번째 줄에서는 총 체스판의 행의 수(N), 열의 수(M), 만들어야하는 체스판의 규격(KxK)의 값을 입력받는다.
• 두번째 줄 부터 N 줄까지 현재 체스판의 상태를 입력 받는다. (블랙의 경우 'B', 화이트의 경우 'W')
• 모두 입력받았다면 K*K 체스판의 다시 칠해야하는 칸이 최소인 값을 구하면 된다.
• 해당 로직을 글로 설명하긴 어려워서 아래와 같이 그림을 포함해서 정리해봤다.
  
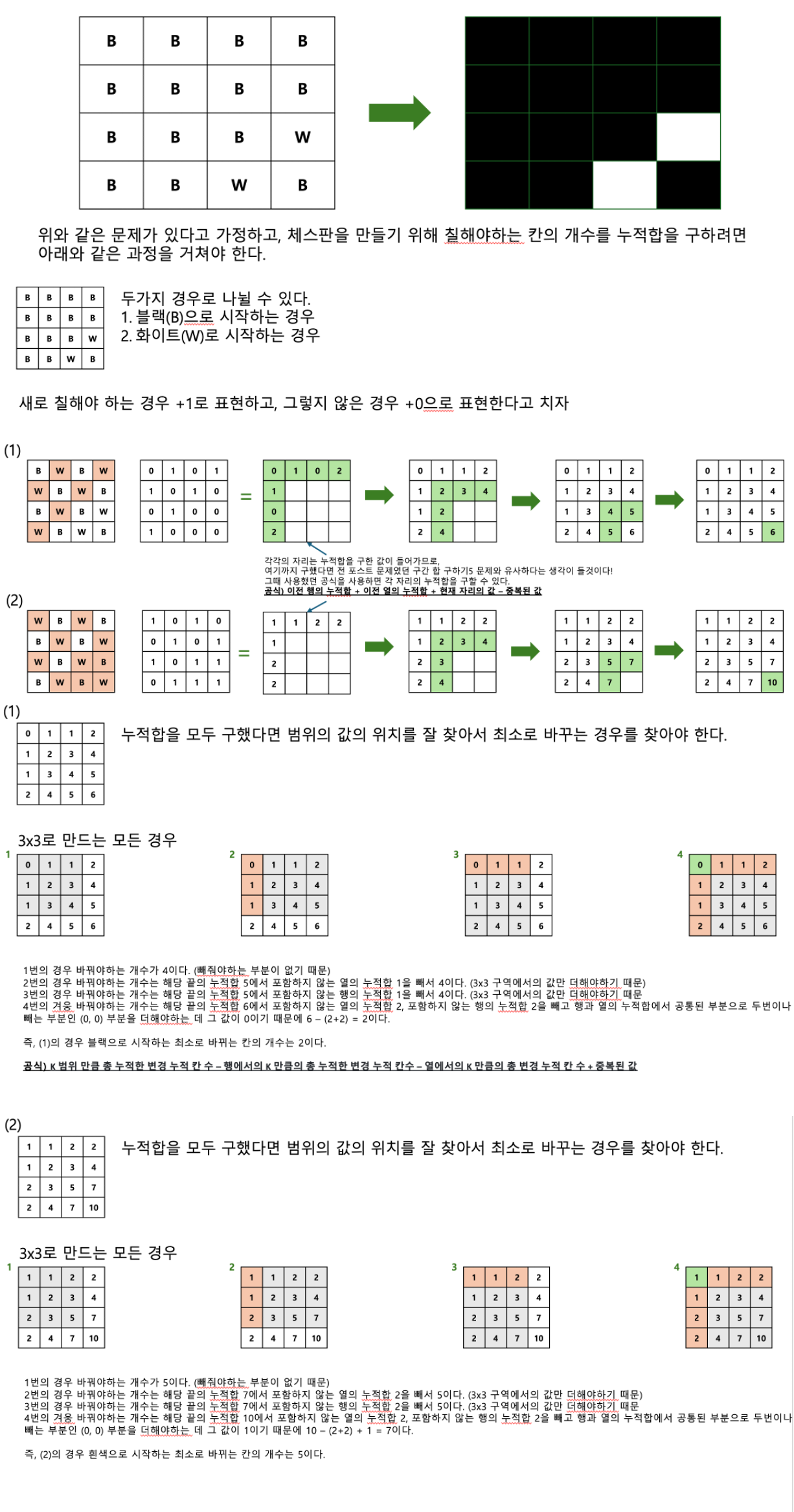
• 로직대로라면 식은 2가지가 나온다.

1. 누적합 공식

	이전 행의 누적합 + 이전 열의 누적합 + 현재 자리의 값 – 중복된 값
    temp[i-1][j] + temp[i][j-1] + + currentValue- temp[i-1][j-1]

2. 체스판 자르는 공식

	K 범위 만큼 총 누적한 변경 누적 칸 수 – 행에서의 K 만큼의 총 누적한 변경 누적 칸수 – 열에서의 K 만큼의 총 변경 누적 칸 수 + 중복된 값
    -> sum[i + K][j + K] - sum[i + K][j] - sum[i][j + K] + sum[i][j]

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int N, M, K;
    static char[][] chessBoard;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken()); //입력받는 체스판의 행
        M = Integer.parseInt(st.nextToken()); //입력받는 체스판의 열
        K = Integer.parseInt(st.nextToken()); //만들어야하는 체스판(K*K)

        chessBoard = new char[N][M];

        char[] tmp;

        for(int i = 0; i < N; i++){
            tmp = br.readLine().toCharArray(); //한줄씩 입력받아서 해당 문자들을 문자열 1차원 배열로 넣음
            for(int j = 0; j < M; j++) {
                chessBoard[i][j] = tmp[j]; //체스판에 하나하나씩 넣음
            }
        }

        int[][] prefixSumBlack = prefixSum('B'); //블랙으로 시작하는 체스판의 누적합(전체)
        int[][] prefixSumWhite = prefixSum('W'); //화이트로 시작하는 체스판의 누적합(전체)

        System.out.println(Math.min(cutChessBoard(prefixSumBlack), cutChessBoard(prefixSumWhite)));
    }

    //체스판 KxK로 자르기
    private static int cutChessBoard(int[][] prefixSum){
        int result = Integer.MAX_VALUE;
        for(int i = 1; i <= N-K+1; i++){
            for(int j = 1; j <= M-K+1; j++){
                int num = prefixSum[i+K-1][j+K-1] - prefixSum[i-1][j+K-1] - prefixSum[i+K-1][j-1] + prefixSum[i-1][j-1];

                result = Math.min(num, result);
            }
        }
        return result;
    }

    //체스 누적합 구하기
    private static int[][] prefixSum(char color){
        int[][] tmp = new int[N+1][M+1];

        for(int i = 0; i < N; i++){
            for(int j = 0;  j < M; j++){
                //현재가 블랙인지 화이트인지에 따라 결정 (해당 파라미터 color에 맞춰 바꿔야하는 경우 1 아닌 경우 0)
                int currentValue = 0;

                if((i+j) % 2 == 0){ //체스판의 격자를 균등하게 칠하기 위해
                    //->(i + j) % 2가 0이면, i와 j의 합이 짝수이므로 짝수 행과 짝수 열이 모두 같은 색으로 칠해짐
                    currentValue = chessBoard[i][j] == color ? 0 : 1;
                }else{
                    currentValue =  chessBoard[i][j] != color ? 0 : 1;
                }

                tmp[i+1][j+1] = tmp[i+1][j] + tmp[i][j+1] - tmp[i][j] + currentValue;
            }
        }
        return tmp;
    }
}

결과

느낀 점

진짜 오래걸린 문제이다. 문제 자체를 이해를 했지만 이를 코드에 녹여내는 부분에서 애를 많이 먹었다... 이렇게 누적합문제는 다 풀었지만 아직 많이 부족한 것 같아서 계속해서 리마인드해야할 것 같다.