백준 2798 블랙잭 [JAVA]

Ga0·2023년 4월 11일

Java baekjoon 백준 자바

baekjoon

목록 보기

26/137

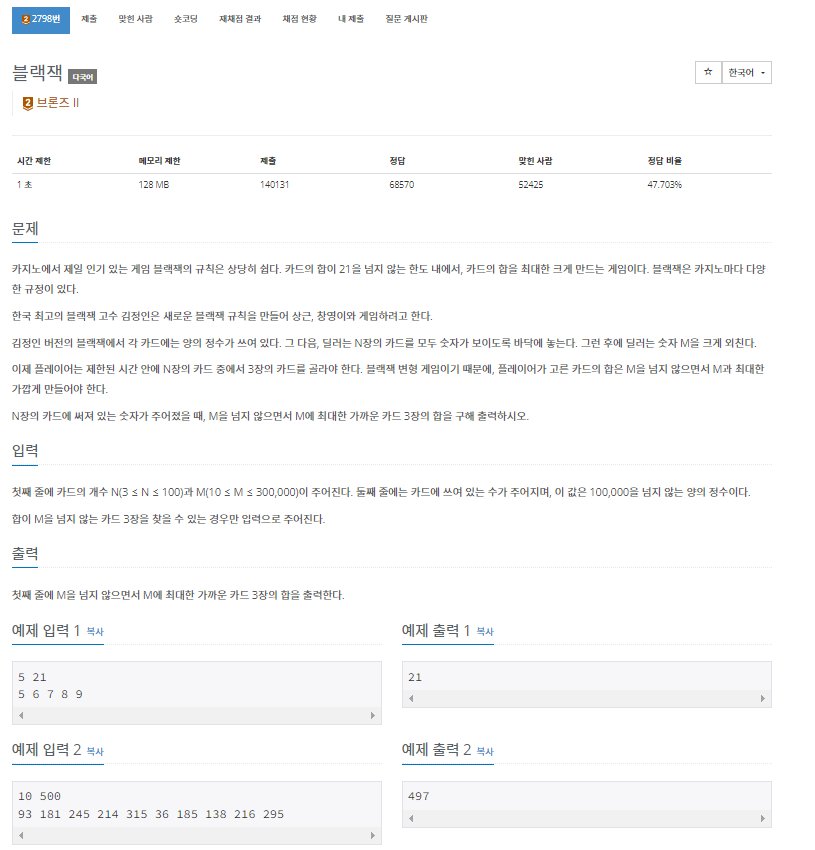
문제 해석

문제가 요구하는 바는 간단하다.
콘솔로 부터 첫째줄에는 카드 개수(N)과 기준이 되는 수(M : 이 값을 기준으로 가까운 3개의 숫자를 입력받아아함)를 입력받는다.
둘째 줄에서는 입력받은 카드의 개수만큼 수를 입력받아, M과 슈 3개를 더했을 때 M과 가장 가까운 수의 합을 출력하면 되는 문제이다.

틀린 코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int [] numberArray = new int[N];

        st = new StringTokenizer(br.readLine());
        br.close();

        for(int i = 0; i < N; i++) {
            numberArray[i] = Integer.parseInt(st.nextToken());
        }

        int sum = 0; //3수의 합을 구하는 변수
        int temp = 0; //근사치를 저장하여 저장하는 변수 (이전 for문의 3개의 합을 더해서 계속 비교해준다.

        for(int i = 0; i < N-2; i++) { //숫자가 겹치면 안되기 때문에 i는 0부터 시작하고 N-2까지
            for(int j = i+1; j < N-1; j++) { // 다음 j는 i+1 부터 시작하고 N-1까지
                for(int k = j+1; k < N; k++) { //다음 k는 j+1부터 시작 N까지 반복
                    sum = numberArray[i] + numberArray[j] + numberArray[k]; //3수를 합쳐서
                    if(Math.abs(M - temp) >= Math.abs(M - sum)){ //3개의 합을 더하고 M에서 뺐을때의 값이 작을 수록 근사치
                        temp = sum;
                    }
                }
            }
        }
        bw.write(temp + "\n");
        bw.flush();
        bw.close();

    }
}

로직

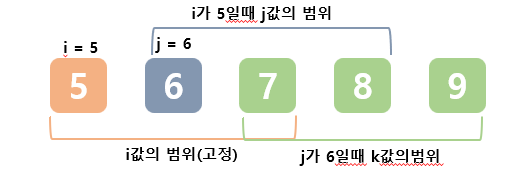
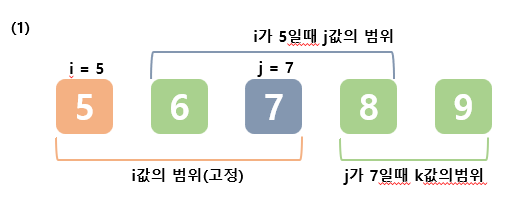
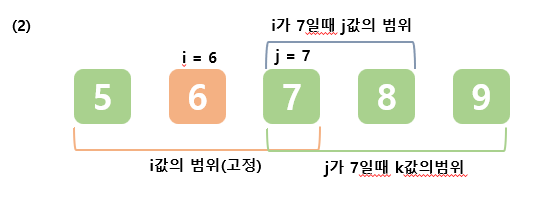
여기서 생각하기에 핵심 로직은 for문인데, i의 반복문 범위 값과 j의 반복문 범위 값, k의 반복문 범위값을 각각 다르게 하여, 절대 같은 값을 가질 수 없도록 하였다.
이러한 기준으로 반복하기 때문에 3개의 수가 겹칠 수 없는 구조가 만들어진다.

결과1

맞게 로직을 짠 것 같은데... 또 틀렸다고 나온다...
뭐가 문제일까?
어떤 부분에서 틀리는 건지 이해하고 싶다...

참고 코드

https://okeybox.tistory.com/203

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int [] numberArray = new int[N];

        st = new StringTokenizer(br.readLine());
        br.close();

        for(int i = 0; i < N; i++) {
            numberArray[i] = Integer.parseInt(st.nextToken());
        }

        int sum = 0; //3수의 합을 구하는 변수
        int temp = 0; //근사치를 저장하여 저장하는 변수 (이전 for문의 3개의 합을 더해서 계속 비교해준다.

        for(int i = 0; i < N-2; i++) { //숫자가 겹치면 안되기 때문에 i는 0부터 시작하고 N-2까지
            for(int j = i+1; j < N-1; j++) { // 다음 j는 i+1 부터 시작하고 N-1까지
                for(int k = j+1; k < N; k++) { //다음 k는 j+1부터 시작 N까지 반복
                    sum = numberArray[i] + numberArray[j] + numberArray[k]; //3수를 합쳐서
                    if(sum > temp && sum <= M){ //이전 근사치보다 큰데 M보다 작거나 같다는 것은 이전 근사치보다 M에 가깝다는 뜻
                        temp = sum;
                    }
                }
            }
        }
        bw.write(temp + "\n");
        bw.flush();
        bw.close();

    }
}

이 참고한 코드 내용은 Math.abs()를 쓰지 않고 비교연산자를 사용했다.
이전 근사치 값보다 크고, M보다는 작거나 같다는 것이 이전 근사치 값보다 M에 가깝다는 것을 정의하여 코드로 풀어쓰신 것 같다.

결과2

결과는 맞았습니다.가 나왔지만, sum값이 이미 M일 경우도 반복을 계속하기 때문에, 코드가 비효율적인 것 같아서 함수로 빼보려고 한다!

코드2(함수ver)

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int [] numberArray = new int[N];

        st = new StringTokenizer(br.readLine());
        br.close();

        for(int i = 0; i < N; i++) {
            numberArray[i] = Integer.parseInt(st.nextToken());
        }
        bw.write( blackjack(numberArray, N, M) + "\n");
        bw.flush();
        bw.close();

    }

    public static int blackjack(int[] arrays, int N, int M){
        int sum = 0; //3수의 합을 구하는 변수
        int temp = 0; //근사치를 저장하여 저장하는 변수 (이전 for문의 3개의 합을 더해서 계속 비교해준다.

        for(int i = 0; i < N-2; i++) { //숫자가 겹치면 안되기 때문에 i는 0부터 시작하고 N-2까지
            for(int j = i+1; j < N-1; j++) { // 다음 j는 i+1 부터 시작하고 N-1까지
                for(int k = j+1; k < N; k++) { //다음 k는 j+1부터 시작 N까지 반복
                    sum = arrays[i] + arrays[j] + arrays[k]; //3수를 합쳐서
                    if(sum == M){ //수가 이미 같으면 바로 return 한다.
                        return sum;
                    }
                    if(sum > temp && sum <= M){ //이전 근사치보다 큰데 M보다 작거나 같다는 것은 이전 근사치보다 M에 가깝다는 뜻
                        temp = sum;
                    }
                }
            }
        }
        return temp; // 완전히 같은 수가 없을 때는 temp(가장 근사치)반환
    }
}