문제 해석
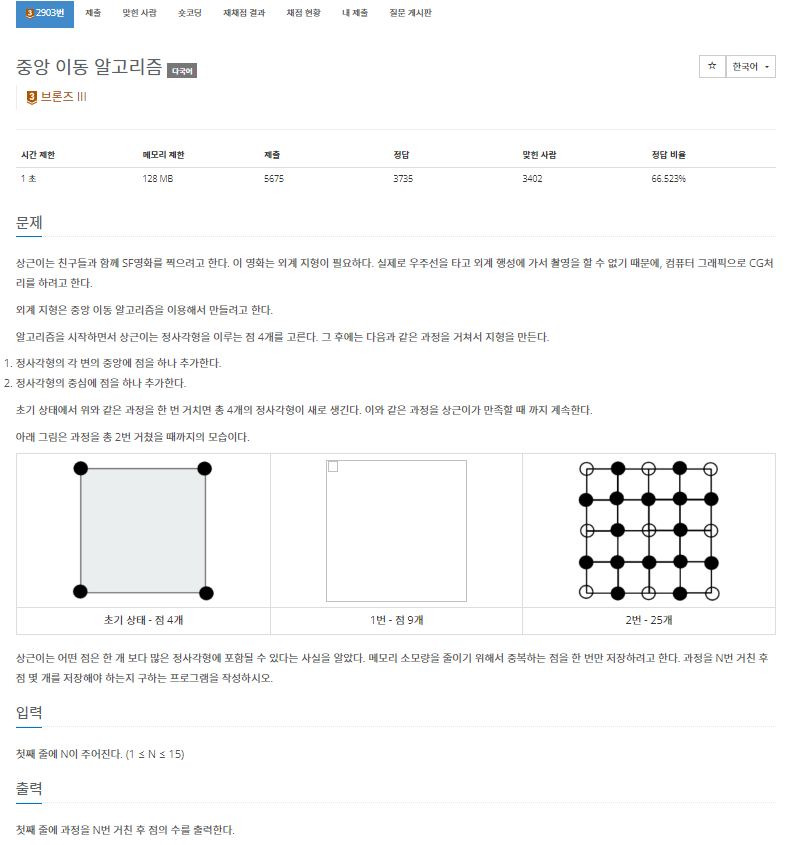
- 문제가 요구하는 바는 간단하다. 입력받은(N) 번 반복하여 N번째의 점이 몇개인지 출력하면 되는 문제이다.
- 점을 찍는 로직(?)은 점과 점이 이어만든 변의 가운데에 점을 찍고 새로찍은 점들의 중심에 또 점을 찍는다.
- 즉, 한 사각형당 점이 5개 추가되는 셈이다. (중복되는 것을 고려 안했을때)
-
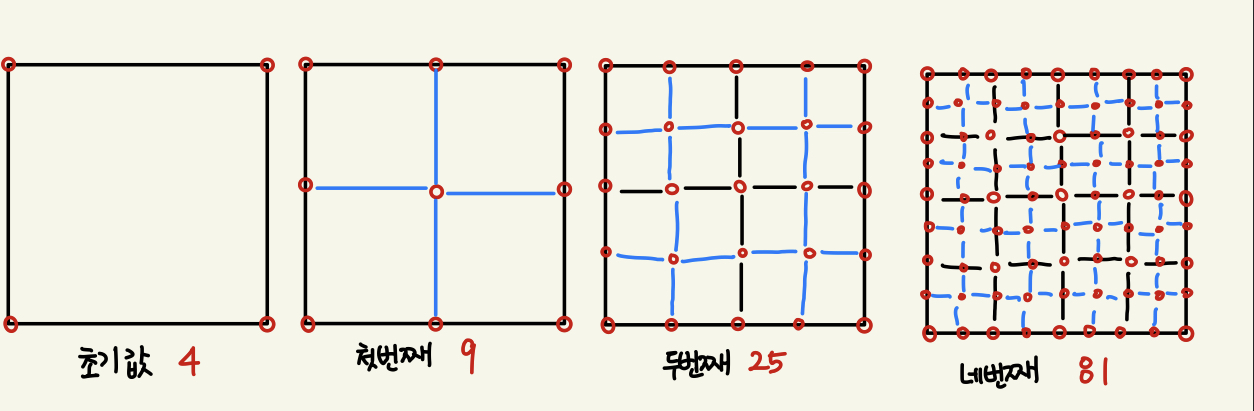
문제를 이해하기 위해 4번째까지 그려보았다.
-
규칙성을 찾아보니 제곱인 것을 알 수 있고, 한 변에 있는 점의 개수의 거듭제곱인 것이 눈에 보인다.
- 초기값엔 한 변에 점이 2개이니까 2의 2승
- 첫번째 중앙 이동 알고리즘을 돌았을 땐한 변에 점이 3개이니까 3의 2승
- 두번째 중앙 이동 알고리즘을 돌았을 땐한 변에 점이 5개이니까 5의 2승
- 세번째 중앙 이동 알고리즘을 돌았을 땐한 변에 점이 9개이니까 9의 2승
- 이렇게 거듭제곱을 한다는 것을 알 수 있다.
-> 그렇다면, 한변에 있는 점이 어떠한 규칙으로 도는지를 확인을 해야한다!
-
2 -> 3 -> 5 -> 9 ... 식으로 증가했다. (증가 값은 1, 2, 4...이다)
-
위의 공식으로는 정확히 확신할 수는 없는데, 그리기엔 시간이 걸리고 임의로 한변에 점이 몇개 들어갈지 세어보았더니 이다음 식도 2, 3, 5, 9, 17, 33... (1, 2, 4, 8, 16...일 것이다) => 예제로 준 값이 5번째가 1089이라고 했으니까 33x33이 1089임으로 아마 맞다고 확신한다!
-> 즉, 다시 말해! 2진수 비트값이 증가하는 것처럼 증가한다. 2의 0승, 2의 1승, 2의 2승, 2의 3승 식으로
공식
총 점의 개수 = (2^n + 1)^2 => (2의 n승 + 1)의 제곱
-> 2의 0승은 1인데, 초기는 2가 나와야하고
-> 2의 1승은 2인데, 첫번째는 3이 나와야해서 +1을 해주었다.
코드
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
br.close();
// Math의 클래스의 pow()메서드를 사용했다.
// Math.pow(거듭제곱할 숫자, 거듭제곱(몇제곱인지);
System.out.println((int)Math.pow(Math.pow(2, n) +1, 2));
}
}결과

느낀점
- 규칙성을 찾는게 개인적으로 시간이 꽤 걸려서, 많이 연습해야겠다 싶었다..
