백준 9663 N-Queen [JAVA]

문제 해석

• N-Queen 문제는 전에 8-Queen 문제로 한 번 접해본 적이 있다.
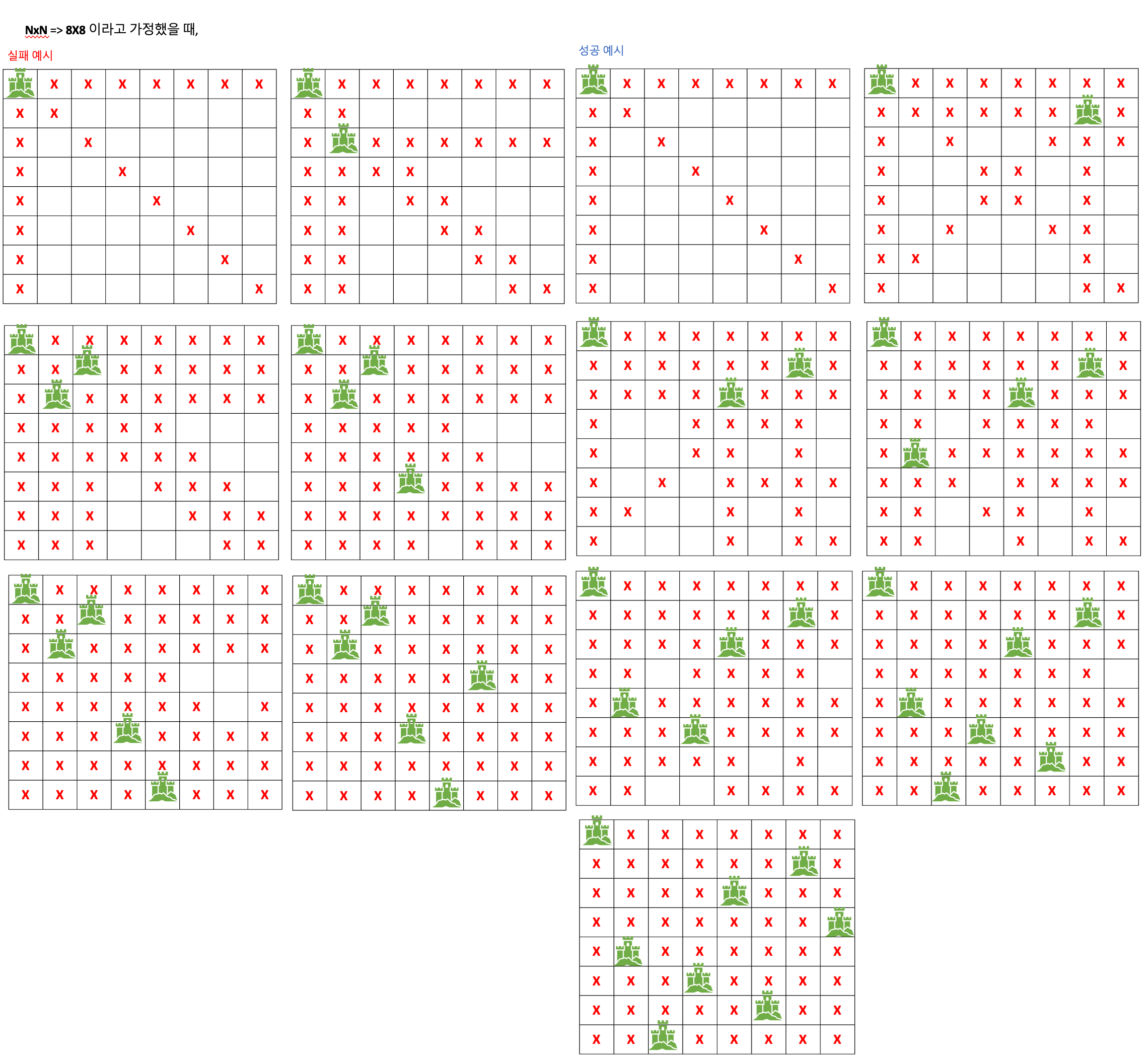
• NxN으로 된 판이 있다고 가정하고, 퀸을 놓을 때 놓은 자리로 부터 행과 열, 동일한 대각선에 존재하면 안되는 문제이다.
• 즉, 서로 공격할 수 없게 만든 모든 경우의 수를 출력하면 되는 문제이다.
• 그림으로 설명하면 아래와 같다.
  

코드

import java.io.*;

public class Main {

    static int N; // N
    static int resultCount; //게임 경우의 수
    static int[] board; //퀸을 놓는 배열(판) = 게임판

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        N = Integer.parseInt(br.readLine()); //N

        board = new int[N]; //판 초기화(크기)

        backTracking(0); // 배열에 저장할 열 인덱스만 파라미터로 넘긴다.
        br.close();
        System.out.println(resultCount);
    }

    static void backTracking(int queenCount) {
        if (queenCount == N) { //퀸을 N개 모두 놓았으면 경우의 수를 하나 증가시킨다.
            resultCount++; //경우의 수 증가
            return;
        }

        for(int i = 0; i < N; i++) {
            board[queenCount] = i;
            // 놓을 수 있는 위치일 경우 재귀호출
            if (checkQueen(queenCount)) {
                backTracking(queenCount + 1);
            }
        }

    }

    //해당 열자리에 퀸을 놓을 수 있는지 확인하는 메소드
    static boolean checkQueen(int col){
        for (int i = 0; i < col; i++) {
            // 해당 열의 행과 i열의 행이 일치할경우
            /*
             아래와 같이 가정을 하고
             -1 -1  -1  -1
             -1 -1  -1  -1
             -1 -1  -1  -1
             -1 -1   3  -1

             board[col] => (2,3) => 열이 인덱스 값이고 행이 넣은 값 2이라고 생각(1차원 배열이기 때문)
             board[3] = 2이라고 가정 (= 2라고 가정한 점은 열의 인덱스가 2인 행을 비교한다고 생각하면 됨)
             => 이미 행은 결정된 상태이므로 여기서 계산

             for(int i = 0; i < 3; i++)
              board[3] == board[0] : 2 == -1 ? false
              board[3] == board[1] : 2 == -1 ? false
              board[3] == board[2] : 2 == -1 ? false
              => 즉, 반복문이 돌때까지 걸리지 않았으므로 같은 행에 있는 건 없다.
            */
            if (board[col] == board[i]) {
                return false;
            }


            // 현 자리에서 동일한 대각선에 위치한 경우
            /*
                (0,0) (1,0) (2,0) (3,0)
                (0,1) (1,1) (2,1) (3,1)
                (0,2) (1,2) (2,2) (3,2)
                (0,3) (1,3) (2,3) (3,3)

                => 규칙을 보면 같은 대각선에 위치한다고 판별하는 기준이 행과 열의 차가 같은 값이 동일한 대각선이다.
                   예를 들어, (0,0)과 동일한 대각선에 위치한다는 기준은
                   (1,1), (2,2), (3,3)도 행과 열의 차가 0으로 같다.
                   또, 예를 들면 (1,0)과 같은 대각선은 차가 1인 것인데
                   (2,1),(0,1),(3,2),(1,2 : 차피 같은 열이다.)이 있다.
                   * 중요한 포인트는 그냥 뺀게 아니라 절대값(수의 차이)이다.
            */
            else if (Math.abs(col - i) == Math.abs(board[col] - board[i])) {
                return false;
            }
        }
        return true;
    }
}

• 코드 설명은 주석으로 작성해두었다.

결과

느낀 점

• 전에 우연히 이 문제를 접해서 푼 적이 있었는데... 막상 풀려하니까 생각이 안났다...(확실히 그땐 그냥 푸는 것에 급급해서 로직을 깊이 생각할 기회가 없었던 것 같다..) 리뷰 필수인 이유...😭