분할 정복(Divide and Conquer)
- 분할: 해결하기 쉽도록 문제를 여러 개의 작은 부분으로 나누는 것
- 정복: 나눈 작은 문제를 각각 해결한다.
- 통합: (필요한 경우에는) 해결된 해답을 모은다.
1. 이분 검색 (Binary Search)
재귀적 방식
- 찾으려는 데이터(
data)가 배열의 중간의 항목과 같으면 찾음, 그렇지 않은 경우 아래의 과정 수행 - 분할: 배열을 반으로 나누어서
data가 중앙에 위치한 항목보다 작으면 왼 중앙을 기준으로 왼쪽의 배열 반쪽을 선택, 그렇지 않으면 중앙을 기준으로 오른쪽 배열 반쪽을 선택 - 정복: 반쪽 배열에서
data를 검색 - 통합: 필요하지 않음
재귀로 구현된 이분 검색 코드(python)
s = [1,2,4,6,7,9,10]
data = 10
def binarySearchRecursion(low,high):
if low > high:
return -1
else:
mid = (high+low)//2
if(data == s[mid]):
return mid
elif(data < s[mid]):
high = mid -1
else:
low = mid+1
return binarySearchRecursion(low,high)참고) 재귀 알고리즘
- 재귀호출이 알고리즘의 마지막에 이루어 질 때를 tail recursion이라고 한다.
- 이러한 tail recursion은 iterative algorithm 으로 변환하기가 수월하다.
- 사실상 재귀라는 것은 사람이 편하기 위해서 만든 것이며, 모든 재귀는 반복문으로 변환할 수 있다.
- 재귀는 데이터를 stack에 저장해놓기 때문에 때에 따라 반복문보다 매우 느리게 동작할 수도 있다.
재귀를 쓰지 않은 이분 검색 코드(python)
s = [1,2,4,6,7,9,10]
data = 10
def binarySearchNonRecursion(low, high):
while(low <= high):
mid = (low + high)//2
if(data == s[mid]):
return mid
elif(data > s[mid]):
low = mid+1
else:
high = mid-1
return -1최악의 경우 시간 복잡도 분석
-
경우 1) 반쪽 배열의 크기가 n/2일때
이고,
반복 대입법을 통해
...
-
경우 2) 일반적인 경우 - 반쪽 배열의 크기는 개
(아래에서 는 밑이 2인 로그)
위에서 구한 결과를 바탕으로 임을 수학적 귀납법으로 증명
귀납 출발 : 이면
귀납 가정 : 이고, 인 모든 에 대해서 , 이 성립한다고 가정
귀납 단계
1) n이 짝수이면
-> 귀납가정에 의해서
-> n이 짝수이므로
2) n이 홀수이면 로 증명
3) 따라서
2. 합병 정렬 (Merge Sort)
- 분할 : 배열을 반으로 나눈다.
- 정복 : 나눠진 배열을 정렬한다.
- 통합 : 정렬된 배열들을 하나의 배열로 다시 통합한다.
재귀를 사용한 합병 정렬 코드(python) - 공간복잡도 O(2n)
def merge_sort(n, s):
if n == 1:
return
h = n // 2
m = n - h
u = s[:h]
v = s[h:]
merge_sort(h, u)
merge_sort(m, v)
merge(h, m, u, v, s)
def merge(h, m, u, v, s):
i = j = k = 0
while i < h and j < m:
if u[i] < v[j]:
s[k] = u[i]
i += 1
else:
s[k] = v[j]
j += 1
k += 1
if i == h:
while j < m:
s[k] = v[j]
j += 1
k += 1
else:
while i < h:
s[k] = u[i]
i += 1
k += 1재귀를 사용하지 않은 합병 정렬 코드(python)
최악의 경우 시간 복잡도 분석
-
시간 복잡도 분석
는 를 정렬하는데 걸리는 시간 은 를 정렬하는데 걸리는 시간, 은 합병하는데 걸리는 시간
재현식은 이고 조건은 이다.
도사정리 2번을 적용하면 -
증명
for with
...
공간복잡도 분석
- 제자리 정렬 알고리즘(in-place-sort): 추가적인 저장장소를 사용하지 않고 정렬하는 알고리즘
- 합병 정렬은 제자리 정렬 알고리즘이 될 수 없다.
- 위에서 언급한 재귀를 사용한 합병정렬 코드는 공간 복잡도가 O(2n)인 알고리즘이다.
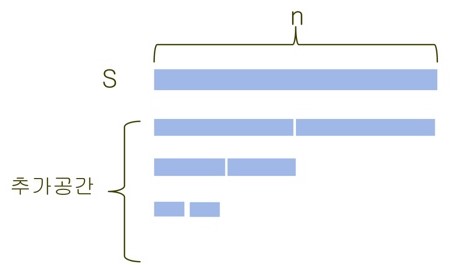
- 위의 코드에서
mergeSort()함수를 수행함에 따라 새로운 추가공간인U와V를 할당하게 된다. - 처음 배열의 크기가 n이라면, 첫 재귀 호출에서 n개 다음호출에서 n/2, n/4 ... 이므로 등차수열의 합을 통해 2n임을 구할 수 있다. ()
- 해당 방식을 개선하여
mergeSort()함수에서 복사하는 내용을 없애면, O(n)인 알고리즘으로 만들 수 있다.
- 위의 코드에서
공간복잡도 개선된 합병 정렬 코드 - 공간 복잡도 O(n)
- 해당 코드에서는
U라는 합병할 때 사용하는 하나의 배열을 만들고 시작하기 때문에U의 크기인 n만큼의 공간만 차지하면 하위 합병 과정에서는U를 사용하여 공간 복잡도가 O(n)이 된다.
def mergeSort2(s, low, high): #데이터를 copy 하는 과정이 없다.
mid = 0
if(low < high):
mid = (low+high)//2
mergeSort2(s,low,mid)
mergeSort2(s,mid+1, high)
merge2(s,low,mid,high)
def merge2(s, low, mid, high):
i = low
j = mid + 1
k = 0
U = s[low:high+1] #합병시 사용하는 하나의 배열만 존재
while i <= mid and j <= high:
if s[i] < s[j]:
U[k] = s[i]
i += 1
else:
U[k] = s[j]
j += 1
k += 1
while i <= mid:
U[k] = s[i]
k += 1
i += 1
while j <= high:
U[k] = s[j]
k += 1
j += 1
idx = 0
while low <= high:
s[low] = U[idx]
low += 1
idx += 13. 빠른 정렬 (Quick Sort)
특징
- not stable : 데이터가 동일한 key 인 경우에 정렬하고 나서 원래 순서가 달라지는 경우
- 실제로 절대적으로 빨라서 빠른 정렬 알고리즘은 아니다. 분할교환정렬(partition exchange sort)이 더 맞는 용어
빠른 정렬 코드 (python)
def quickSort(s,low,high):
if(high>low):
pivotPoint = partition(s,low,high)
quickSort(s,low,pivotPoint-1)
quickSort(s,pivotPoint+1,high)
def partition(s,low,high):
pivotItem = s[low]
j=low
for i in range(low+1, high+1):
if(s[i] < pivotItem):
j+=1
temp = s[j]
s[j] = s[i]
s[i] = temp
pivotPoint = j
temp = s[pivotPoint]
s[pivotPoint] = s[low]
s[low] = temp
return pivotPoint
s=[3,5,2,9,10,14,4,8]
quickSort(s,0,7)
print(s)최악의 경우 시간 복잡도 분석
- 입력이 비내림차순으로 정렬되어있는 경우
- partition 알고리즘에서 첫번째 항목만 제외하고 모든 항목을 비교하기 때문에
- 재현식은 :
- 재현식을 풀면
->
->
->
평균의 경우를 고려한 시간 복잡도 분석
- A(n)이 n개의 데이터를 정렬하는데 걸리는 평균 시간
- pivot item이 p번째 데이터가 될 확률 1/n, 기준점이 p일때 두 부분배열을 정렬하는데 걸리는 평균시간은 [A(p-1) + A(n-p)], 분할하는데 걸리는 시간은 n-1
- 평균적인 시간 복잡도는
- =
- =
- 양변에 n을 곱하고 n 대신 n-1 대입
- 정리하면
- 결과적으로
- =
- 위의 식에서 우변은 매우 작으므로 무시
- 좌변을 근사하면 ln => 2ln
- 결론적으로 = =
- quick sort는 평균적으로 의 알고리즘
4. 행렬 곱셈
단순한 행렬곱셈 알고리즘
- 시간복잡도를 계산하면 : n x n 행렬의 곱셈 ->
- 총 8번의 곱셈과 4번의 덧셈 필요 ->
쉬트라센 방법
- n x n 행렬에서(n은 짝수) 각 행렬을 4개의 부분행렬로 나누고 계산하는 방식
- 곱셈과 덧셈을 나눠서 까지 나타냄
- 7번의 곱셈과 18번의 덧셈/뺄셈 필요
- 행렬의 크기가 커질수록 효율적인 방법
- 위의 식을 전개하면
5. 큰 정수 계산법
단순 곱셈
- 단순곱셈의 경우 시간 걸림, 덧셈은 1차 시간에 완료 가능
방법 1
- n이 큰 정수의 숫자의 개수,
- ex)
라고 하면, - 결과적으로 자리곱셈 4번(xw, xz, wy, yz) 으로 바뀜
방법 1의 최악의 경우 시간복잡도 분석
- 이고 n이 2의 거듭제곱 형태
- 재현식을 풀면
- 결론적으로 단순 곱셈 보다 빨라지지 않음
방법 2 (방법 1의 개선된 형태)
- 이전의 방법 1 에서는 의 계산이 필요
- 이라는 계산을 추가
- -> 곱셈 한번
- -> 곱셈 두번
- 결론적으로 곱셈의 수를 한번 줄일 수 있음
큰 정수 계산법 방법 2 코드(python)
import math
def prod2(u,v):
n = max(len(str(u)), len(str(v)))
if(u == 0 or v == 0):
return 0
elif (n <= 4):
return u*v
else:
m = math.floor(n/2)
x = u // 10**m
y = u % 10**m
w = v // 10**m
z = v % 10**m
r = prod2(x+y, w+z)
p = prod2(x,w)
q = prod2(y,z)
return p*10**(2*m) + (r-p-q)*(10**m) + q방법 2의 최악의 경우 시간복잡도 분석
prod2(x+y, w+Z),prod2(x,w),prod2(y,z)- 위의 세 번의 연산을 해야하기 때문에
6. 임계값 결정
- divide and conquer 방법에서 큰 문제를 어느 크기의 문제가 될 때까지 분할할 것인가
- 합병정렬과 교환정렬 중 어떤 임계값에서 어떤 정렬을 선택해야 하는가..
- merge sort2의 경우
- 분할하고 재합병하는데 걸리는 시간 으로 가정
- 단순화 시키면, , n>1, n은 2의 거듭제곱
- =>
- 교환정렬의 경우
- 그렇다면 어느 지점에서 합병정렬에서 교환정렬로 바꿔 계산하는 것이 빠른가
- 를 만족하는 n ?
- n < 591의 결과가 나온다. 그러나 이 경우, 은 문제 크기가 1이 될 때 까지 분할한 경우의 복잡도 이므로 틀린 분석
- 정확한 분석
- 합병정렬에서 교환정렬로 넘어가는 그 지점을 찾아야 한다!
- 를 풀면 t가 짝수인 경우 t=128, 홀수인 경우 t = 128.008 이 정확한 threshold 이다.
7. 분할 정복을 사용하지 말아야 하는 경우
- 크기가 n인 입력이 2개 이상의 조각으로 분해되며, 분할된 부분의 크기가 거의 n에 가깝게 되는 경우 -> 시간 복잡도가 지수 시간인 경우
- ex)
- 크기가 n인 입력이 거의 n개 이상의 조각으로 분해되며, 분할된 부분의 크기가 n/c인 경우(c는 상수) -> 시간 복잡도
- ex)
8. 도사 정리
공식
- , (n>1이고, n이 b의 거듭제곱)
예시
인 경우
->
-> 공식 2번째 case에 해당한다
-> 결론 :
