RL- Markov Decision Process

1. Introduction

Core Concept of Reinforcement

• concept is the strengthening of a behavior pattern
• pleasure oriented
• subfield of AI and Machine Learning
• Key Component of Reinforcement Learning
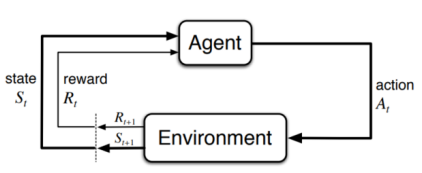
  • Agent : 학습을 시키는 주체
  • Environment : 주어진 환경
  • State : 환경의 상태
  • Action : agent가 선택한 행동
  • Reward : agent가 action을 한 이후의 보상
  • Policy : 상황이 주어졌을때 어떻게 행동해야 할지에 대한 것
  • Value function : state에 대한 평가를 위해 예상되는 기대 reward
• 강화학습의 목표 : learn an optimal policy
  • Optimal Policy : 기대되는 cumulative reward를 최대화 하는 정책
• agent는 직접 해봐야 알 수 있음
• RL loop
  • agent가 현재 state에서의 environment를 observe 한다. (observation)
  • observation에 기반하여, 현재 policy를 따르는 action을 선택한다.
  • agent는 선택한 action을 하여 environment를 바꾼다.
  • agent는 action의 결과를 통해 environment로 부터 reward와 새로운 observation을 받는다.
  • agent는 reward와 observation 한 정보를 통해 knowledge(policy, value function, action-value function)를 업데이트
  • 종료 조건에 도달할 때 까지 반복

2. Finite Markov Decision Process

Markov Decision Process (MDP)

• agent가 좋은 행동을 하도록 만드는 framework
• A MDP decision process
  • S : state
  • A : Action
  • P : Probability
    • $P_a(s,s') = Pr(S_{t+1}=s'|s_t=s, a_t=a)$
    • state와 action이 결정되었을 때, $s_{t+1}$이 $s'$이 될 확률
  • R : Reward
    • $s$에서 $a$를 해서 $s'$으로 갔을 때 받는 reward
• MDP goal
  • policy function $\pi$
  • 좋은 policy를 찾기!

The Agent-Environment Interface

• trajectory : $S_0\ A_0\ R_1\ S_1\ A_1\ R_2\ S_2\ A_2\ R_3...$
• $p(s',r|s,a)\doteq Pr(S_t=s', R_t=r|S_{t-1}=s,A_{t-1}=a)$
  • t-1 에서 state가 s이고 action이 a일 때 t에서 state는 s'이고 reward가 r일 확률
  • $S_t\ R_t$의 값은 $S_{t-1}\ R_{t-1}$ 값에만 의존한다.
  • state는 미래를 위해서 과거의 agent와 environment의 상호작용에 대한 모든 정보를 가지고 있어야 한다. => Markov Property
  • $p(s_{t+1},r_{t+1}|s_0,a_0,r_1,s_1,a_1, ... ,r_{t-1},s_{t-1},a_{t-1},r_t,s_t,a_t)=p(s_{t+1},r_{t+1}|s_t,a_t)$
• Markov Property를 사용하는 이유
  • 과거의 모든 state를 고려하지 않고 가장 최근의 state와 action만을 이용하므로 공간을 절약할 수 있다.
  • 사용 예시) chess, inventory management
• State transition and Reward function
  • dynamic function : $p(s'r|s,a)$
  • state-transition probability function $(p:S\times S\times A)$
    • $p(s'|s,a)\doteq Pr(S_t=s, A_{t-1}=a)$
  • expected rewards for state-action $(p:S\times A)$
    • $r(s,a)\doteq E[R_t|S_{t-1}=s,A_{t-1}=a]=\sum_{r\in R}r\sum_{s'\in S}p(s',r|s,a)$
  • expected rewards for state-action-next state $(p:S\times A \times S)$
    • $r(s,a,s')\doteq E[R_t|S_{t-1}=s,A_{t-1}=a, S_t=s']=\sum_{r\in R}r\frac{p(s',r|s,a)}{p(s'|s,a)}$

3. Markov Property and State Design

• real-world problem에서는 Markov property가 적합하지 않다.
• 현재 state만 가지고 agent가 어떤 상태인지 알 수 없다. (이전 state의 내용이 필요하다)
  • More information이 필요하다.
    -> state 구성함에 있어서 필요한 것
    • snaphot of a particular point : 현재 state의 정보
    • piece of information : 이전 state가 가지고 있던 데이터의 일부
    • $S_t$를 구성하기 위해서 frame t-3, t-2, t-1의 정보를 사용한다면, 이전 state가 없어도 정보를 얻을 수 있다.

4. MDP-Goals and Rewards

Maximizing Rewards

• Reward ($R_t$) : agent의 action을 수행하면 environment에서 주는 보상값(scalar)이다.
• agent는 reward를 최대로 만들기 위해 학습을 한다.
  -> 이때 문제를 잘 설정하고 reward를 잘 주는 것이 가장 중요한 문제이다.

5. MDP-Returns and Episodes

Maximizing Cumulative Reward over Episodes

• RL의 목표를 long term으로 본다면, 누적된 reward를 극대화 하는 것으로 볼 수 있다.
• expected return $G_t$
  • $G_t\doteq R_{t+1}+R_{t+2}+...+R_T$ ($T$는 final step)
• Episode
  • sequence of actions, states and rewards
  • agent는 episode를 반복해서 좋은 결과를 찾게 된다.
  • 문제점
    • 예를 들어 $G_t$가 둘 다 100일 때 goal 까지 가는 경로에 있어서 하나는 금방 도달했지만, 다른 하나는 돌아가서 오래 걸렸다고 했을 때, 둘 중 누가 더 좋은 방식인지 아직까지는 알 수가 없다!

6. MDP-Return Discounting

• 위에서 언급한 문제를 해결하기 위해서 discount factor가 등장한다.
• discount factor
  • $\gamma$ : 0~1의 값으로 횟수를 나타낸다.
  • $G_t\doteq R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}...$
    -> $G_t \doteq R_{t+1}+\gamma G_{t+1}$
  • discount factor가 클수록 미래에 보상에 높은 가중치를 주는 것이며, 낮을수록 단기 보상이 큰 것을 의미한다.
• discount factor를 사용하는 이유
  • Modeling uncertainty
  • Fast convergence
  • Finite tasks
• discount factor를 사용하지 않을 때의 문제점
  -> 미래와 현재 보상에 대해 같은 가중치를 부여하게 된다.
  • Slow convergence
  • Infinite returns
  • Overemphasis on long-term consequences

7. MDP-Policies and Value Functions

• Policy $(\pi)$
  • agent가 어떤 action을 선택할지 정해주는 것
  • Deterministic policy
    • 각 state에서 action이 정해져 있음, no randomness
    • $a=\pi(s)$
  • Stochastic policy
    • agent가 action을 확률에 따라 선택함
    • $P(a|s)=\pi(a|s)$
• Value Function
  • estimate expected cumulative rewards or expected return
  • 행동의 가치를 평가하는 것 -> agent가 올바른 행동을 했는지 확인할 수 있다.

8. MDP-Value Functions

State-value function (V-function)

• $v_{\pi}(s)\doteq E_\pi[G_t|S_t=s]$
• 의미: state $s$에서 시작해서 $\pi$에 따라 행동했을 때 얻는 expected return
• 예시) 도서관에 있을때의 가치

Action-value function (Q-function)

• $q_\pi(s,a)\doteq E_\pi[S_t=s, A_t=a]$
• 의미: state $s$에서 시작해서 action $a$를 하고 $\pi$에 따라 행동했을 때 얻는 expected return
• 예시) 수업($s$)이 끝나고 -> 도서관을 갔을($a$) 때의 가치

Experience

• agent의 경험은 state, action, reward에 따라서 업데이트 된다.
• action의 결과로 state에 있어서 reward와 transition을 observe하여 value function을 더 좋은 방향으로 업데이트 한다.
• value function을 만드는데 사용하는 방식들에 MC와 TD가 있다.

Monte Carlo methods

• value function을 업데이트 하는 방식 중 하나
• MC는 완료된 episode를 통해 동작한다.
• state와 action의 수가 너무 많으면 MC는 적합하지 않다.
  -> 완료된 episode를 다 확인해야 하기 때문..

Bellman Equation

$v_\pi(s)\doteq E_\pi[G_t|S_t=s]=E_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s]$
$=\sum_a\pi(a|s)\sum_{s'}\sum_r p(s',r|s,a)[r+\gamma E_\pi[G_{t+1}|S_{t+1}=s']]$
$=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')]$

9. MDP-Optimal Policies and Value Functions

optimal policy