
네오는 평소 프로도가 비상금을 숨겨놓는 장소를 알려줄 비밀지도를 손에 넣었다. 그런데 이 비밀지도는 숫자로 암호화되어 있어 위치를 확인하기 위해서는 암호를 해독해야 한다. 다행히 지도 암호를 해독할 방법을 적어놓은 메모도 함께 발견했다.
지도는 한 변의 길이가 n인 정사각형 배열 형태로, 각 칸은 "공백"(" ") 또는 "벽"("#") 두 종류로 이루어져 있다.
전체 지도는 두 장의 지도를 겹쳐서 얻을 수 있다. 각각 "지도 1"과 "지도 2"라고 하자. 지도 1 또는 지도 2 중 어느 하나라도 벽인 부분은 전체 지도에서도 벽이다. 지도 1과 지도 2에서 모두 공백인 부분은 전체 지도에서도 공백이다.
"지도 1"과 "지도 2"는 각각 정수 배열로 암호화되어 있다.
암호화된 배열은 지도의 각 가로줄에서 벽 부분을 1, 공백 부분을 0으로 부호화했을 때 얻어지는 이진수에 해당하는 값의 배열이다.
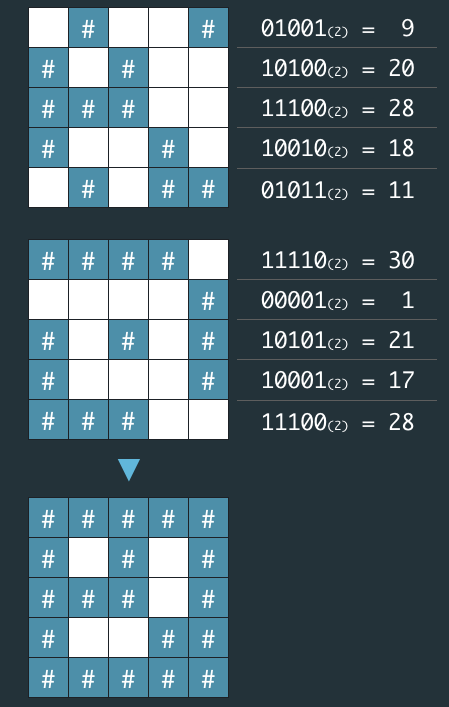
네오가 프로도의 비상금을 손에 넣을 수 있도록, 비밀지도의 암호를 해독하는 작업을 도와줄 프로그램을 작성하라.
입력 형식
입력으로 지도의 한 변 크기 n 과 2개의 정수 배열 arr1, arr2가 들어온다.
1 ≦ n ≦ 16
arr1, arr2는 길이 n인 정수 배열로 주어진다.
정수 배열의 각 원소 x를 이진수로 변환했을 때의 길이는 n 이하이다. 즉, 0 ≦ x ≦ 2n - 1을 만족한다.
출력 형식
원래의 비밀지도를 해독하여 '#', 공백으로 구성된 문자열 배열로 출력하라.
입출력 예제
| 매개변수 | 값 |
|---|---|
| n | 5 |
| arr1 | [9, 20, 28, 18, 11] |
| arr2 | [30, 1, 21, 17, 28] |
| 출력 | ["#####","# # #", "### #", "# ##", "#####"] |
| 매개변수 | 값 |
|---|---|
| n | 6 |
| arr1 | [46, 33, 33 ,22, 31, 50] |
| arr2 | [27 ,56, 19, 14, 14, 10] |
| 출력 | ["######", "### #", "## ##", " #### ", " #####", "### # "] |
나의 풀이
function solution(n, arr1, arr2) {
/*
arr1,2의 배열의 값을 뽑아낸 다음 각각 이진수로 바꿔줌
길이에 맞게 앞에 0을 넣어 줌.
0은 공백, 1은 #으로 바꿔줌
두 배열을 비교, 한쪽이라도 #이 있으면 #, 둘다 공백이면 ''인출
*/
return arr1.map((v,i)=> (v.toString(2) * 1 + arr2[i].toString(2) * 1+'')
.padStart(n, '0')
.replace(/0/g,' ')
.replace(/[1-2]/g,'#'))
/* 이진수로 바꾸어 두 값을 숫자로 변환한 다음 더해줌
n자리수를 만드는데 모자란 길이만큼 앞에 0을 더해줌
0은 공백으로, 1이나 2는 #으로 변환
*/
}위쪽은 문제를 보며 생각한 풀이 방식이고, 아래는 바꾼 풀이 방식이다. 처음에는 자릿수를 맞춘 다음 공백과 #으로 바꾸어서 둘을 비교하려고 했는데, 둘을 하나씩 뽑아서 비교하는 방식이 복잡할 것 같았다.
그래서 생각을 바꿨다. 이진법으로 바꾼 다음 두 숫자를 더한다면, 0인 부분은 양 배열의 빈 부분이고 1이나 2 부분은 벽 부분일 것이다. 그래서 숫자로 바꾸어 더한 다음 자릿수를 맞추어 주고 0은 공백으로, 1과 2는 #으로 바꾸어 줬다.
여기서 새로 알게된 함수는 padStart()함수이다. padStart()함수에 인수로 자릿수와 교체할 숫자를 넣어주면, 자릿수에 모자라는만큼 앞부분에 숫자를 넣어 준다.
참고할 풀이
var solution=(n,a,b)=>a.map((a,i)=>(a|b[i]).toString(2).padStart(n,0).replace(/0/g,' ').replace(/1/g,'#'))나와 다른 점은 |을 사용했다는 점이다. 이것은 비트연산자 OR또는 Bitwise OR이라고 부른다. 이진법으로 바꾸어 \양쪽을 비교했을 때, 둘중의 하나라도 1이면 그 비트에 1을 반환한다. 예를 들어 2|3 = 3이다. 2은 이진법으로 10, 3은 2진법으로 11이기 때문에 첫번째 자리에도 11, 즉, 3을 반환하는 것이다. 이것과 비슷한 개념으로 &이 있다.비트연산자 AND 또는 Bitwise AND라고 부른다. 이진법으로 바꾸어 계산하는 것은 똑같은데 양쪽 비트를 비교해서 둘다 1이어야 그 자리에 1을 반환한다. 예를 들어, 2&3 = 2이다. 10과 11을 비교했을 때, 맨 앞자리만 둘 다 1이므로 10을 반환한다. 이 문제가 의도한 함수인 듯 하다.
