[자료구조와 알고리즘] 정렬

지수·2021년 9월 1일

자료구조와 알고리즘

목록 보기

7/12

이 글은 한양대 김경환 교수님 강의를 정리했음을 먼저 밝힙니다.

추가로 같이보면 좋은 자료 : ratsgo's blog for textmining 정렬 알고리즘 비교

📖 정렬이란?

1. 정렬의 정의

✅ 주어진 데이터를 일정한 기준에 따라 순서대로 나열하는 것

숫자 : 사전식 순서 또는 크기를 기준으로 나열
문자 : 사전식 순서에 따라 나열

2. 정렬 방법

오름차순(ascending) : 작은 것에서 큰 것으로, 오래된 것부터
내림차순(descending) : 큰 것에서 작은 것으로, 최근 것부터
단일 키(single key) : 하나의 정렬 기준으로
복합 키(multi key) : 두 개 이상의 정렬 기준으로

3. 정렬 관련 용어 정리

집합(set) : 정렬할 데이터 셋 전체
원소(element) : 데이터 섯의 datum
부분 집합(subset) : 전체 데이터셋을 어떤 기준으로 분할한 일 부분

키(key) : 정렬의 기준이 되는 특정 값
비교(comparison) : 정렬 = 크기 또는 순서를 비교하는 것
이동(move) : 비교의 결과에 따라 위치 재조정
교환(swap) : 두 개 원소의 자리를 서로 맞바꿈

시간복잡도(time complexity) : 알고리즘 수행에 필요한 연산의 수(CPU Time)
공간복잡도(space complexity) : 알고리즘 수행에 필요한 메모리의 크기

분할정복(divide&conquer) : 커다란 데이터셋을 MECE 규칙에 따라 작게 분할하여 계산
병합(merge) : 두 개 부분집합을 입력 받아 하나의 합집합을 출력하는 연산
피벗(pivot) : 회전축, 축, 중심 / 재귀적으로 실행할 때 매 단계의 기준이 되는 원소
기수(radix) : 10진수 체계에서는 기수가 10, base라고도 함
최선(best case) : 가장 좋은 성능을 보이는 경우
최악(worst case) : 가장 좋지 않은 성능을 보이는 경우
안정성(stability) : 알고리즘의 실행 결과를 신뢰할 수 있는 정도

4. 정렬과 이진탐색

이진 탐색 (Binary Search)

정렬된 데이터에 대해서 O(logN)의 성능을 보이는 탐색 알고리즘
정렬된 데이터 중 하나를 집어 올리면 그 왼쪽 부분 집합의 원소는 그보다 작은 값
오른쪽 부분 집합의 원소는 그보다 큰 값

ㄴ 데이터 정렬의 이유 = 빠르게 찾기 위해서

ㄴ 데이터 정렬 = 이진탐색이 가능하도록 데이터 나열

5. 정렬 알고리즘의 목표

ㄴ 복잡도를 줄이고

메모리 사용량(공간복잡도)과 CPU 사용시간(시간복잡도)를 줄이는 것이 목표
일정 수준에 다다르자 복잡도를 줄이는 것에 한계 봉착
알고리즘의 한계는 하드웨어로 해결(큰 메모리와 싸고 빠른 CPU의 등장..!)

ㄴ 안정성은 높이고

알고리즘은 일관된 실행결과를 보장해야함
그런데, 일부 알고리즘은 최악의 경우, 최선의 경우에 따라 그 결과가 많이 다름
약간의 성능을 포기하더라도 안정적인 정렬 결과를 보장해야함

📖 정렬의 종류

시간복잡도에 따라 O(N2) 계열, O(N * logN) 계열로 분류
실행방법에 따라 Comparison Sort(비교 기반 정렬), Distribution Sort(분포 기반 정렬)로 분류
실행하는 메모리에 따라 Internal Sort(내부 정렬), External Sort(외부 정렬)로 분류

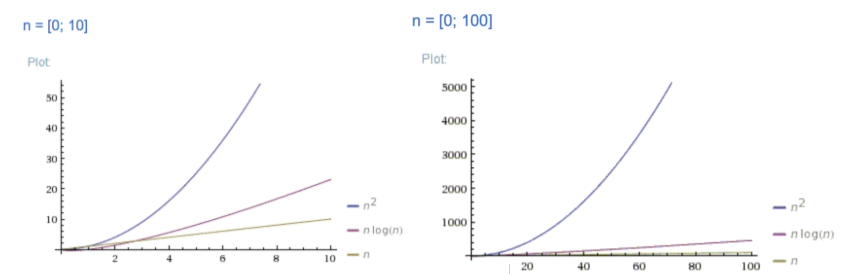
+) 원소 개수가 10일 때, 100일 때 O(N2)과 O(N * logN) 비교
▶ 원소의 개수가 많아질수록 격차가 큼 (n2이 큰 격차로 시간 복잡도가 큼)

1. O(N2) 계열

⏺ 계산 시간이 정렬할 원소의 수의 제곱에 비례
⏺ 지수 함수에 비례
⏺ 알고리즘은 직관적이고 쉬움

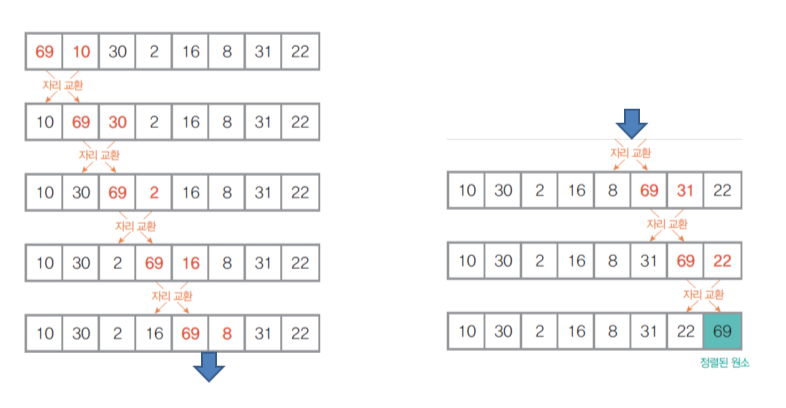
1) 버블 정렬

비교 기반 정렬, 교환 방식
인접한 두 원소를 비교, 자리를 교환하는 방식
끝(가장 큰 값)에서부터 채워짐

정렬 대상 원소 선정
- 이전 단계에서 정렬된 원소를 제외한 모든 원소가 정렬 대상
- 정렬된 원소는 끝에서부터 채워짐

맨 처음 원소부터 마지막 원소까지 반복
- 인접한 두 원소의 값을 비교하여 자리 교환(swap)
- 반복하다보면 제일 큰 원소가 마지막 자리에 위치하게됨

더 이상 정렬할 원소가 없을 때까지 위 과정 반복

원소의 개수가 n일 때, 최대 $\frac{n(n-1)}{2}$ 번 정렬
거의 모든 상황에서 최악의 성능, 단 이미 정렬된 경우는 최선의 성능
직관적으로 구현하기 쉬운 알고리즘

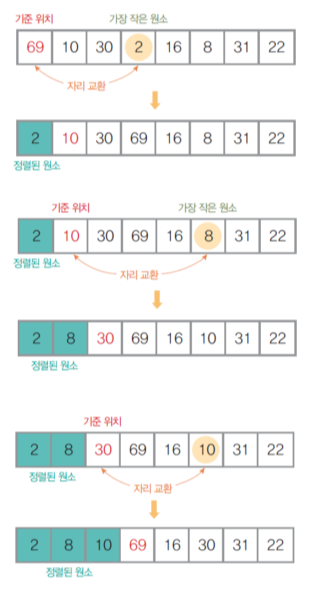
2) 선택 정렬

비교 기반 정렬, 교환 방식
전체 원소들 중에서 기준 원소를 선택, 교환하는 방식
앞(가장 작은 값)에서부터 채워짐

정렬 대상 원소 선정
- 이전 단계에서 정렬된 원소를 제외한 모든 원소가 정렬 대상
- 정렬된 원소는 앞에서부터 채워짐
- 기준 위치 조정

맨 처음 원소부터 마지막 원소까지 반복
- 기준 원소 제외 나머지 원소를 비교하여 가장 작은 원소를 선택
- 선택한 원소가 기준 원소보다 작으면 위치 교환

더 이상 정렬할 원소가 없을 때까지 위 과정 반복

원소의 개수가 n일 때, 일관되게 $\frac{n(n-1)}{2}$ 에 비례하는 시간 소요
버블정렬보다 대략 2배 정도 빠름 (자리 교환을 매 단계 한 번만 하기 때문)
사람이 정렬하는 방식과 가장 유사

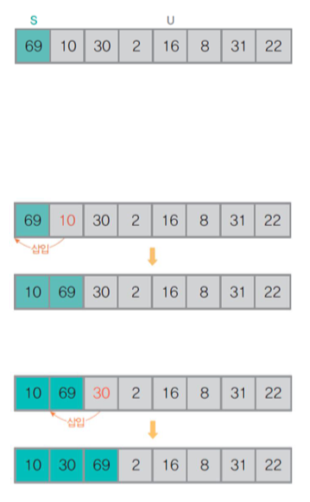
3) 삽입 정렬

비교 기반 정렬, 삽입 방식
정렬된 부분 집합에 정렬할 새 원소의 위치를 찾아 삽입
전체 원소를 정렬된 부분 집합과 정렬되지 않은 부분 집합으로 분할

정렬 대상 원소 선정
- 정렬되지 않은 부분집합에서 원소 한 개를 선택

정렬된 부분 집합에 위 원소를 삽입
- 선택된 원소를 정렬된 부분 집합의 원소들과 비교
- 삽입할 위치를 찾아 삽입

정렬되지 않은 부분 집합이 공집합이 될 때까지 위 과정 반복

O(n2) 계열에서는 평균적으로 빠른 편
구현된 자료구조에 따라 자리 이동 비욜이 클 수 있음(ArrayList 자리 하나씩 미는거 비용 ㄷㄷ)
내림차순 정렬된 데이터셋을 오름차순 정렬할 경우 최악

2. O(N * logN) 계열 (추천🔥)

⏺ 계산 시간이 (원소의 개수*로그값)에 비례
⏺ 밑이 2인 로그함수에 비례
⏺ 알고리즘이 상대적으로 복잡함
🅰 대체로 좋은 성능을 보여주는 알고리즘 그룹

1) 병합 정렬

비교 기반 정렬, divide & conquer 방식
정렬 대상을 먼저 쪼갠 뒤 각각을 정렬
정렬된 부분 집합들을 하나로 결합

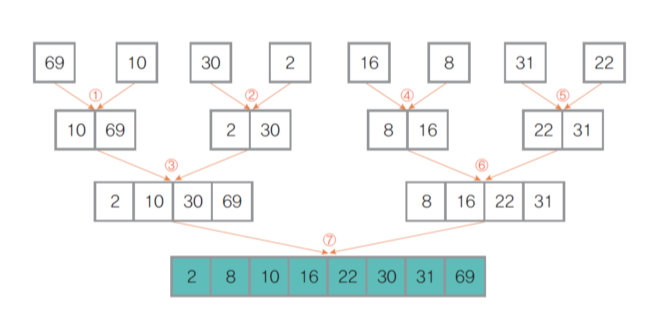
정렬 대상 분할
- 전체 원소를 최소 원소의 부분 집합으로 분할(하나씩 다 뜯어놓음)

분할된 부분 집합 두 개를 정렬하여 하나로 결합
- 각각의 부분 집합은 이미 정렬된 상태 (처음에는 1개씩이고, 이후에는 정렬해서 결합하기 때문에)
- 각 부분 집합의 원소를 하나씩 비교해가면서 정렬

전체 원소가 하나의 집합이 될 때까지 위 과정 반복

최선, 최악의 경우에도 O(n * log2n)으로 일정한 성능
=> 대표적인 stable 알고리즘

2) 힙 정렬

비교 기반 정렬, 트리 방식
정렬 대상 원소들을 Heap Tree에 삽입
Heap Tree의 root를 꺼내와 순서대로 나열

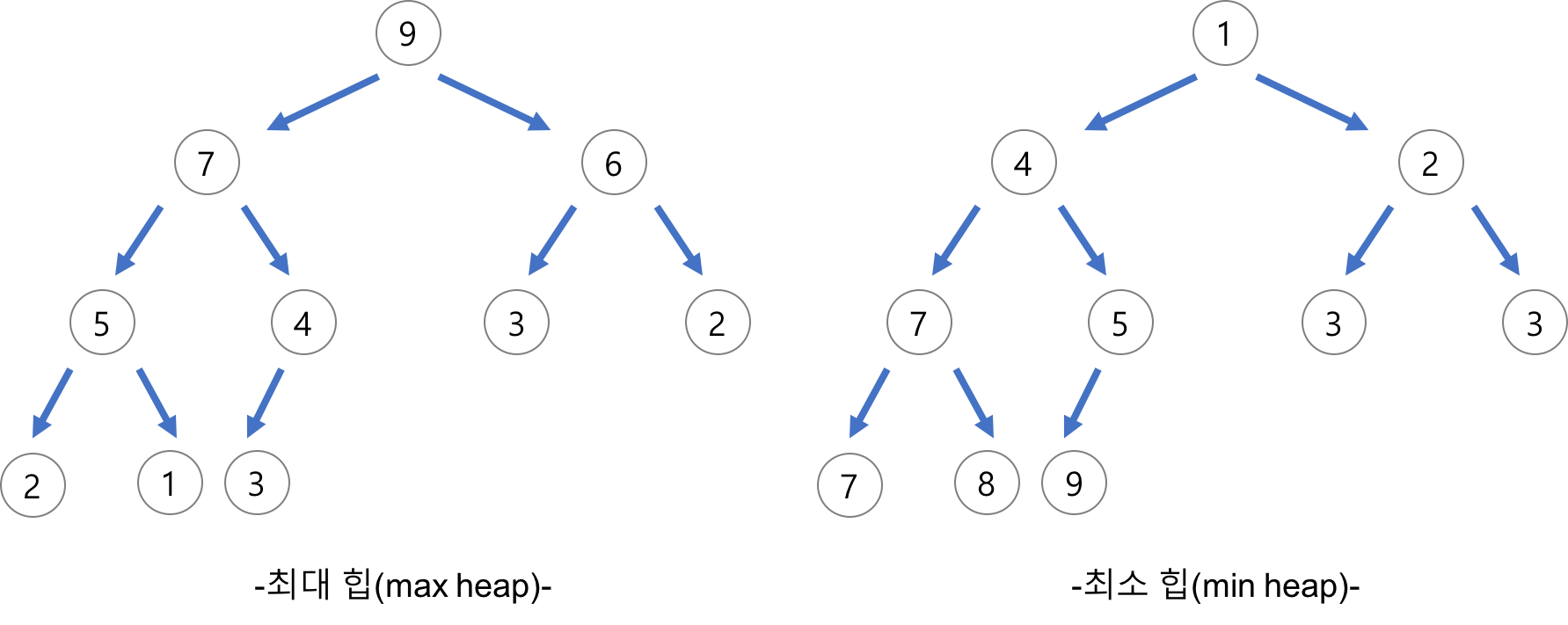이미지 출처 : Heee's Development Blog

정렬 대상을 Heap Tree에 삽입
- 전체 원소를 앞에서부터 차례로 Heap Tree에 삽입

Heap Tree의 root 방문, 제거, 정렬 결과에 배치
- 현재 Heap Tree의 root를 방문, 그 값을 정렬 결과에 배치
- Max Heap인 경우 맨 끝에서부터, Min Heap인 경우 맨 앞에서부터 순회
- 배치 후 root는 제거 → Heap Tree는 알아서 정리 됨

Heap Tree가 empty 상태가 될 때까지 위 과정 반복

최선, 최악의 경우에도 O(n * log2n)으로 일정한 성능
선택 정렬과 유사하나 비교를 직접 구현하느냐 힙트리를 쓰느냐의 차이
휴리스틱이나 하드웨어 가속 등을 적용하지 않고 순수 알고리즘 만으로 구현할 경우 가장 안정적인 성능을 보임

3) 퀵 정렬

비교 기반 정렬, divide & conquer 방식
피벗을 중심으로 왼쪽, 오른쪽 부분 집합을 분할
왼쪽에는 피벗보다 작은 원소를, 오른쪽에는 피벗보다 큰 원소를 이동

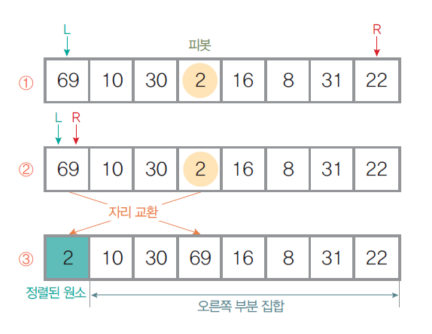
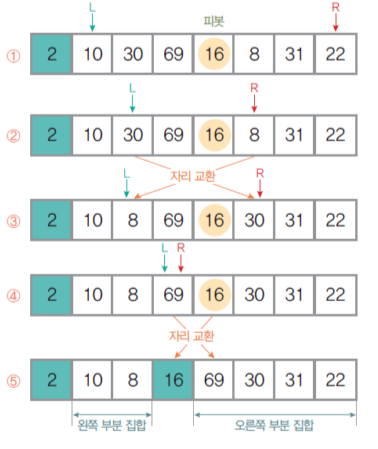
정렬 대상을 왼쪽, 오른쪽 부분 집합으로 구분할 피벗 선택

L, R 원소 찾기와 자리 교환
- 왼쪽 부분 집합의 왼쪽 끝에서 오른쪽으로 순회하며 피벗보다 크거나 같은 원소 L 탐색
- 오른쪽 부분 집합의 오른쪽 끝에서 왼쪽으로 순회하며 피벗보다 작은 원소 R 탐색
- L이 R을 만나면 / R이 L을 만나면 멈춤
- L, R이 있을 경우 서로 교환(swap) 위 과정 반복
- L과 R이 같은 원소에서 만나는 경우, R과 피벗을 교환
- 교환된 자리를 피벗으로 지정한 후 위 과정 반복

모든 부분 집합의 크기가 1 이하가 될 때까지 위 과정 반복

이름과 같이(퀵! 정렬) 평균적인 상황에서 최고의 성능, 컴퓨터 언어로 가장 많이 구현됨
피벗을 어떻게 선정하느냐가 관건, 휴리스틱 즉 직관이 필요

3. 그 밖의 것

안정적이지 않은 시간 복잡도를 갖는 알고리즘
ex) 기수 정렬

지수

사부작 사부작

이전 포스트

[자료구조와 알고리즘] 연결 리스트

다음 포스트