 오랜만에 스압 정리 뚝딱뚝딱...
오랜만에 스압 정리 뚝딱뚝딱...
트리를 정복하자 뚝딱뚝딱...🔧
이 글은 한양대 김경환 교수님 강의를 정리했음을 먼저 밝힙니다.
📖 트리란?
- 이산 수학, 그래프 이론에서 정의하는 트리는 그래프의 특수한 형태로
방향성이 없고(undirected),모든 두 점(vertex)은 하나의 유일한 path로만 연결되어cycle이 없는그래프임
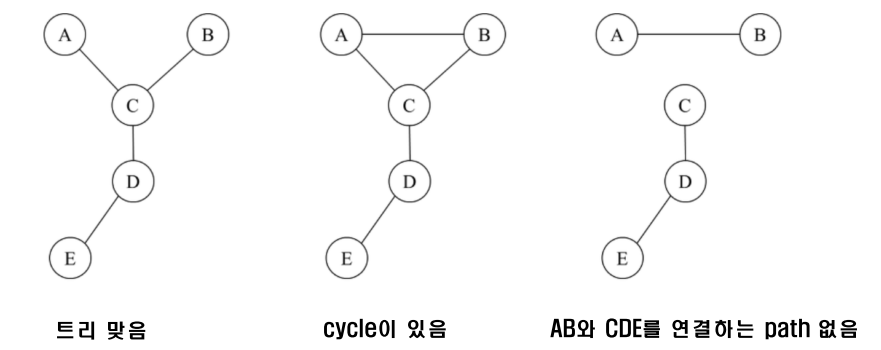
- 자료구조에서 말하는 트리는 Rooted Tree
Rooted Tree: 반드시 하나의 root node로부터 시작- 그래프의 한 종류로 운영체제의 파일시스템, 검색엔진 등에서 널리 사용
- 전산학에서 논하는 자료구조 중 그 변혀잉 가장 많은 자료구조
- 대부분의 경우 배열보다 유연하고 연결리스트보다 효율적
1. 트리의 정의
트리(Tree) 자료구조
- 반드시 하나의 root node로 시작
- root 이후의 노드들은 각각이 트리이면서 교차하지 않음
- 즉, root를 제거하면 여러 개의 트리로 분할됨
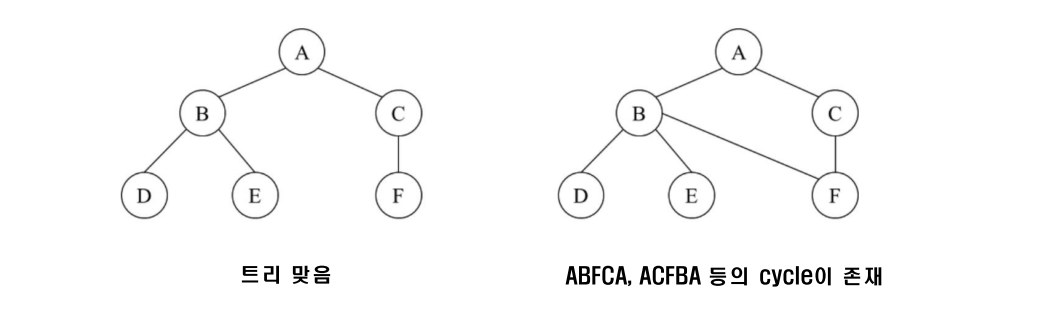
- 왼쪽은 tree가 맞지만, 오른쪽은 트리가 아닌 그래프임
- 방향성이 없다 = 논리적인 순서가 한 쪽 방향으로만 강제되지 않음
2. 트리의 용어
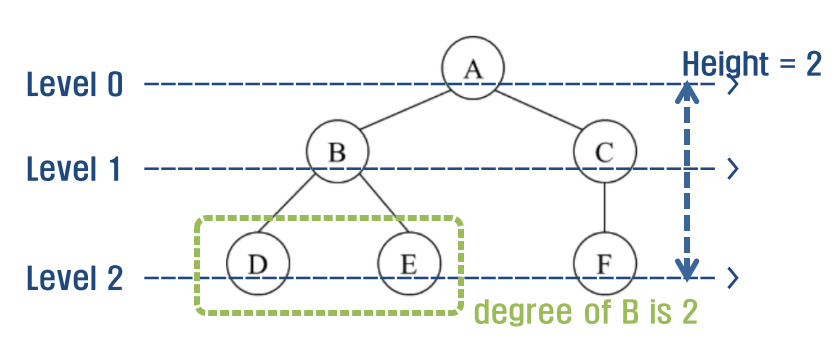
1) 노드(Node)
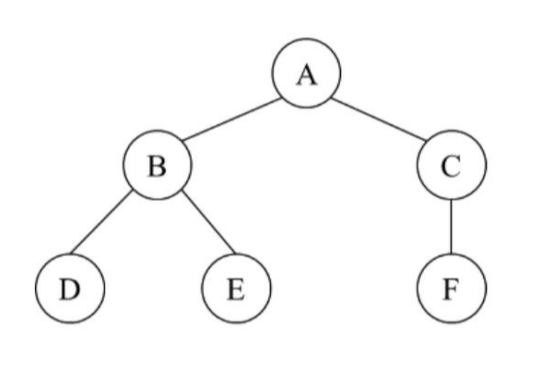
root: 트리의 시작(entry) 노드
(A)parent: 어떤 노드의 직계 상위 레벨의 노드를 지칭
(B는 D,E의 parent, C는 F의 parent, A는 B,C의 parent)child: 어떤 노드의 직계 하위 레벌의 노드를 지칭
(D,E는 B의 child, F는 C의 child, B,C는 A의 child)sibling: parent가 같은 노드들
(D와 E, B와 C는 각각 sibling)leaf: child가 없는 노드
(D,E,F)ancestor: 특정 노드로부터 root에 이르기 까지 부모 노드들
(D의 ancestor는 B,A)edge: 노드와 노드를 연결하는 선
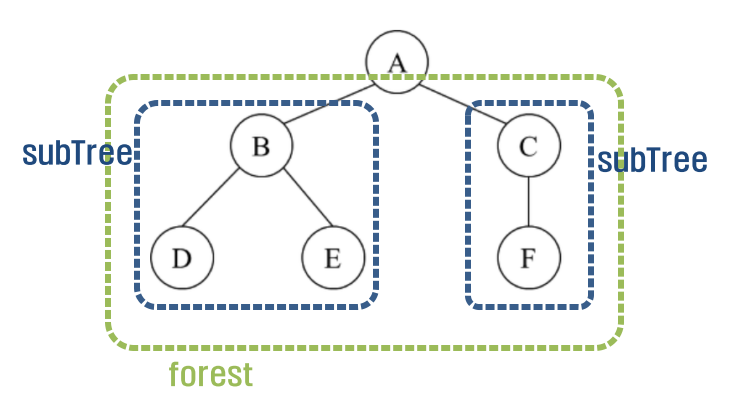
2) SubTree와 Foreat
- 어떤 트리의 root 노드를 제거하면 한 개 이상의
subTree로 분할 - 이 때, 이들 하위 트리들을 원소로 하는 집합을
forest라 함 - 트리에서 root 노드를 제거하여 만들어진 subTree들의 새로운 root는 이전에 sibling 관계
3) 트리의 구조
차수(degree): 한 노드가 가지고 있는 child 노드의 개수Degree of Tree: 트리의 노드들 중 최대 차수깊이(depth): root에서 특정 노드까지 간선의 개수높이(height): 트리에서 가장 깊은 깊이를 그 트리의 높이라 함레벨(level): 같은 깊이에 있는 노드들을 같은 레벨의 노드라 표현경로(path): 한 노드에서 또 다른 노드까지 거쳐가는 노드들의 순서길이(length): 출발 노드에서 도착 노드까지의 노드의 개수
3. 트리의 종류
1) 이진 트리(binary tree)
- 트리의 차수가 2 이하인 트리
- 이진 트리가 아닌 경우는 일반 트리, 또는 그냥 트리라 칭함

<이진트리의 노드 특성>
- 모든 노드의 차수는 2 이하, {0, 1, 2}
- n개의 노드를 갖는 이진 트리의 간선(edge)은 n-l
- 높이가 h인 경우, 노드 수는 최소 h+1, 최대 2^(h+1) -1
- parent와 child의 관계는 1:2로 정의
- child는 left child와 right child만을 가짐
- child가 값이 없는 경우에는 공백(null) 노드로 간주
- root를 제거한 후 생기는 하위트리(subTree)도 이진트리
- 하위트리의 root를 제거한 후 생기는 하위트리 또한 이진트리
=> 재귀적(recursive) 구조 - 한 노드를 제거한 후 생기는 forest의 원소 개수도 2 이하
2) 이진 트리의 종류
포화이진트리(full binary tree): 각 레벨의 구성원이 가득 찬 이진 트리완전이진트리(complete binary tree): 포화이진트리에서 마지막 레벨의 구성원(leaf) 중 일부(끝에서부터)가 부족한 이진 트리편향이진트리(skewed binary tree): 오른쪽이나 왼쪽 한 방향으로 치우친 이진 트리균형이진트리(balanced binary tree): 노드의 양쪽 subTree의 높이 차의 절대값이 1이하{-1,0,1}인 이진 트리- 힙트리(Heap Tree, min-Heap/max-Heap) : 트리의 노드들이 갖는 값 중 최소, 최대값을 root로 하는 이진 트리
이진탐색트리(binary search tree): 노드를 중심으로 왼쪽은 작고 오른쪽은 큰 값이 오도록 만든 이진 트리
4. 이진트리의 순회
1) 순회
- 트리의 모든 노드를 빠짐 없이, 중복 없이 방문하여 그 값을 읽음
- 이진 트리의 노드 : Value, Left subTree and Right subTree →
V, L, R
2) 순회의 방법
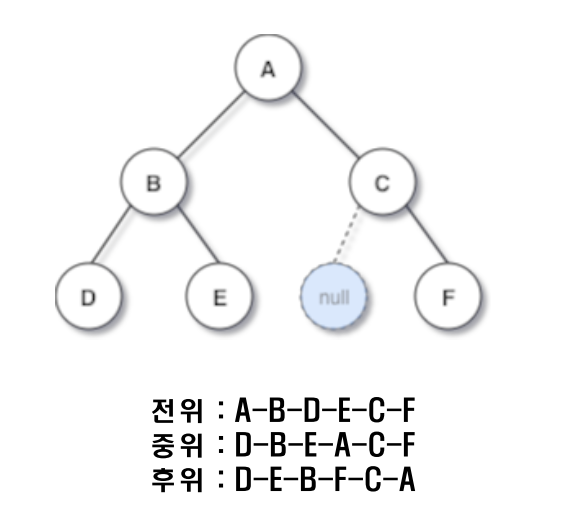
전위순회(Preorder): Value ⇒ 좌측 섭트리(L) ⇒ 우측 섭트리(R)중위순회(Inorder): 좌측 섭트리(L) ⇒ Value ⇒ 우측 섭트리(R)후위순회(Postorder): 좌측 섭트리(L) ⇒ 우측 섭트리(R) ⇒ Value
5. 힙트리
: 최대 최소값을 빠르게 찾기 위한 이진 트리
1) 힙트리의 구조적 특징
- 구조적 특징은 완전이진트리를 따름
= 트리의 마지막 레벨의 노드(leaf)가 끝에서 m개 만큼 부족한, 포화이진트리 변형
2) 힙트리의 내용적 특징
- 내용적 특징은
maxHeap과minHeap으로 나누어 볼 수 있음
-최대힙(maxHeap): 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
-최소힙(minHeap): 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
오랜만에 학부 시절 들었던 🔥자료구조와 알고리즘🔥 강의 필기자료를 꺼내어 복습해보았다.
강의를 들을 때는 가장 힘들었던 수업이었지만 열심히 공부한만큼 가장 뿌듯하고 기억에 남는 수업이 되었는데,
시간이 한 2년 지나니까 기억이 희미해졌다😥 다시 하나씩 꺼내보며 그 때처럼 열심히 공부해야겠다!
