문제 링크
https://www.acmicpc.net/problem/11497
문제 유형
그래프 탐색 - 그리디, DFS/BFS
🌈문제
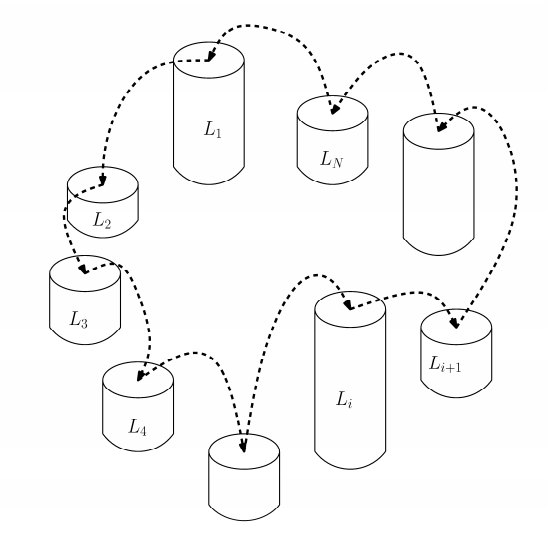
남규는 통나무를 세워 놓고 건너뛰기를 좋아한다. 그래서 N개의 통나무를 원형으로 세워 놓고 뛰어놀려고 한다. 남규는 원형으로 인접한 옆 통나무로 건너뛰는데, 이때 각 인접한 통나무의 높이 차가 최소가 되게 하려 한다.
통나무 건너뛰기의 난이도는 인접한 두 통나무 간의 높이의 차의 최댓값으로 결정된다. 높이가 {2, 4, 5, 7, 9}인 통나무들을 세우려 한다고 가정하자. 이를 [2, 9, 7, 4, 5]의 순서로 세웠다면, 가장 첫 통나무와 가장 마지막 통나무 역시 인접해 있다. 즉, 높이가 2인 것과 높이가 5인 것도 서로 인접해 있다. 배열 [2, 9, 7, 4, 5]의 난이도는 |2-9| = 7이다. 우리는 더 나은 배열 [2, 5, 9, 7, 4]를 만들 수 있으며 이 배열의 난이도는 |5-9| = 4이다. 이 배열보다 난이도가 낮은 배열은 만들 수 없으므로 이 배열이 남규가 찾는 답이 된다.
입력
입력은 T개의 테스트 케이스로 이루어져 있다. 첫 줄에 T가 주어진다.
이어지는 각 줄마다 첫 줄에 통나무의 개수를 나타내는 정수 N(5 ≤ N ≤ 10,000), 둘째 줄에 각 통나무의 높이를 나타내는 정수 Li가 주어진다. (1 ≤ Li ≤ 100,000)
출력
각 테스트 케이스마다 한 줄에 주어진 통나무들로 만들 수 있는 최소 난이도를 출력하시오.
1. 첫 시도 + 아이디어
먼저 통나무의 배열을 오름차순으로 정렬합니다.
서로 오름차순으로 정렬되어 인접한 수와의 높이 차이가 가장 작을 것이라고 생각합니다.
이렇게 정렬을 하게 되면 맨 첫번째의 원소와 마지막의 원소 높이 차이가 가장 크게 발생하므로 이 상황을 없애기 위해서 마지막의 원소를 가운데로 옮기고, 자리를 오른쪽으로 하나씩 밀면서 가장 작은 높이 차이가 발생하는 경우를 찾는 방법을 생각했습니다.
T = int(input())
for _ in range(T):
whatMax = 100000
list2=[]
log=[]
N=int(input())
log= list(map(int, input().split()))
log.sort()
if(log[0]==log[len(log)-1]):
print(0)
continue
log[2],log[len(log)-1]=log[len(log)-1],log[2]
list2.append(abs(log[0] - log[len(log) - 1]))
list2.append(abs(log[0] - log[1]))
for i in range(2,len(log)-1):
for j in range(2,len(log)):
list1.append(abs(log[j]-log[j-1]))
tmp=max(list1)
if whatMax >= tmp:
whatMax = tmp
log[i],log[i+1] = log[i+1],log[i]
list1=[]
list2.append(whatMax)
print(max(list2))모든 Test Case들이 성립하기는 하지만 1초라는 시간 복잡도에 맞지 않아 시간 초과가 발생합니다. 이 방법은 통나무가 존재할 수 있는 모든 경우를 고려하는 경우이지만 효율적인 코드는 아닙니다.
다른 문제풀이법을 고수해야 합니다.
또다른 문제 풀이법은 다음과 같습니다.
먼저, 가장 큰 통나무를 가운데에 배치합니다. 이후 가장 큰 통나무를 기준으로 양 옆에 통나무의 높이 차이가 가장 덜 나는 친구를 배치하면 됩니다.
이 풀이법을 고려하면 최대 인덱스 차이가 나는 것은 겨우 2칸입니다.
정렬한 값에서, 인덱스가 최대 2만큼 차이나는 것만, 최대 높이 차가 될 수 있으니 이를 바탕으로 코드를 작성합니다.
T = int(input())
for _ in range(T):
N = int(input())
logs = list(map(int, input().split()))
logs.sort()
answer = 0
for i in range(2, N):
answer = max(answer, abs(logs[i] - logs[i-2]))
print(answer)