[BOJ] 1707번 - 이분 그래프

문제 링크

https://www.acmicpc.net/problem/1707

문제 유형

DFS/BFS

🌈문제

그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.

2
3 2
1 3
2 3
4 4
1 2
2 3
3 4
4 2

출력

K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

YES
NO

💡 아이디어

끄앙 이 문제 너무너무 어려웠다.
나름대로 풀어보려고 생각을 해보았는데, 먼저 노드의 번호가 1부터 V까지 받을 수 있으니까 그 인덱스를 가지는 이차원 배열을 만든다. 이후 해당 노드에 인접한 노드가 등장하게 되면 해당 인덱스에 노드값을 저장해둔다.

그리고 인덱스를 1부터 검사하여, graph[1]에 들어 있는 노드들을 제외하고 나머지 노드들을 집합의 가능성이 있는 노드라고 판단한다.
이후 남은 노드들을 재귀함수로 돌리면서 그 안에서도 인접한 노드가 있는지 계속 찾고, 찾고, 찾으면 풀이가 될 것이라 생각하였다.

하지만! 해당 문제는 가능한 간선의 개수가 20만개이므로 20만개의 for문을 돌려놓은 것에 그 안에 이중 for문으로 2만개의 for문을 수행하여 총 40만회가 넘는 연산을 진행한다. 시간 복잡도 면에서 비효율적인 풀이이기 때문에 이렇게 풀이하면 올바르지 못하다.
그래서 다른 분들이 어떻게 풀이하셨는지 확인하며 정답을 구해보고자 했다.

풀이는 아래 규칙을 찾아내면 조금 더 쉬워진다.

각 정점(노드)들을 이웃 꼭짓점들과 다른 색으로 계속해서 칠한다. 같은 색깔의 꼭짓점이 서로 연결되어 있는지 확인하면 정답을 구할 수 있다.

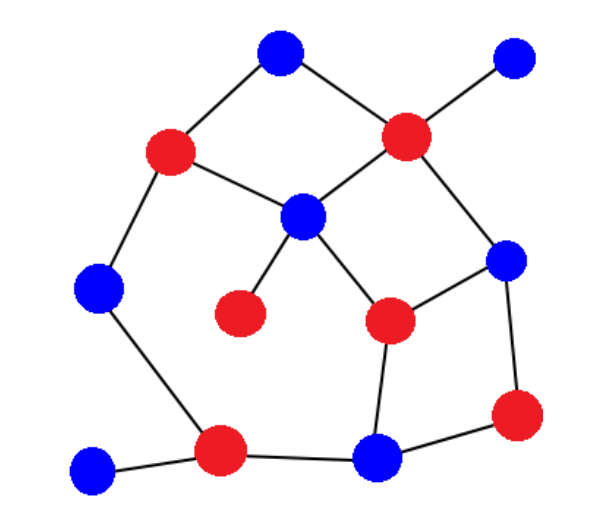
약간 요런 느낌쓰로다가 그래프가 그려질 수 있는지 확인하면 된다.

👨‍💻 코드 작성

먼저 테스트케이스만큼 입력을 받아야 한다. 이 부분은 쉬우니까 모든 노드를 담을 수 있는 graph 리스트를 생성하고 입력받도록 만들어 보자.

for _ in range(T):
    check = 0
    V, E = map(int, input().split())
    global visited
    visited = [0] * (V + 1)
    graph = [[] for _ in range(V + 1)]
    for _ in range(E):
        a, b = map(int, input().split())
        graph[a].append(b)
        graph[b].append(a)

이제 색을 다르게 받을 수 있는 bfs함수를 작성하면 된다.
현재 visited함수는 모든 수를 0으로 초기화해두었다. 만약 0이라면 색 1을 먼저 칠하고, 먼저 칠한 인접한 노드의 색이 달라지게끔만 처리해주면 되는 것이다.

def bfs(start):
    queue = deque([start])
    if visited[start] == 0:
        visited[start] = 1
    while queue:
        v = queue.popleft()
        color = visited[v]
        for i in graph[v]:
            if visited[i] == 0:
                queue.append(i)
                if color == 1:
                    visited[i] = 2
                else:
                    visited[i] = 1
            elif visited[i] == 1:
                if color == 1:
                    print("NO")
                    return False
            elif visited[i] == 2:
                if color == 2:
                    print("NO")
                    return False
    return True

평소 만나는 bfs코드랑 똑같다. 다만 경우에 따라서 색을 다르게 칠해주는 조건만 추가된 것이라고 생각하면 편하다. 만약 색깔이 존재하는데 전에 칠한 색과 동일하다면 False를 리턴하며 NO를 프린트할 수 있게끔 해주면 된다. 방문을 했는데 현재 색과 다르다면, for문을 계속 돌리면서 큐를 비워나간다고 생각하면 된다.
다음으로는 bfs 함수를 사용하는 부분의 코드이다.

for i in range(1, V + 1): #비연결 그래프인 점 고려. 모든 노드 탐색
    if not bfs(i):
       check = 1
       break
if check == 0:
   print("YES")

1번 노드부터 V번 노드까지 모두 고려한다. 해당 문제에서는 그래프가 연결 그래프라는 것을 특정하지 않았기 때문에 비연결 노드까지 모두 고려해서 문제를 풀어야 한다.
만약 bfs함수가 False를 반환하였을 때, NO를 당연히 print할 것이다. 그리고 즉시 돌리던 for문을 종료하면 된다.(정답은 이미 나왔으므로)
만약, 모든 for문을 돌려서 노드를 확인하였는데 한번도 No가 나온 적이 없다면, YES를 출력해주고 다음 테스트케이스로 넘어가면 된다.

노드를 색칠해 나간다는 개념이 조금 어려웠지만, 아이디어를 떠올리기만 하면 일반적인 bfs 공식으로 쉽게 접근할 수 있는 문제이다.