문제 링크
https://www.acmicpc.net/problem/2146
문제 유형
DFS/BFS
🌈문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
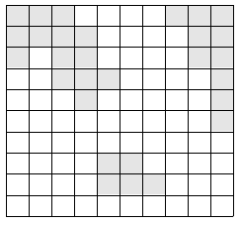
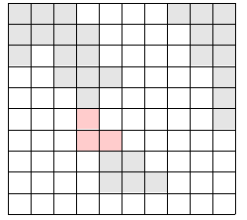
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.
물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
입력
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
10
1 1 1 0 0 0 0 1 1 1
1 1 1 1 0 0 0 0 1 1
1 0 1 1 0 0 0 0 1 1
0 0 1 1 1 0 0 0 0 1
0 0 0 1 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.
3💡 아이디어
해당 문제는 계속 노드들을 탐색해 나가며 최단거리를 구해야 하므로 BFS를 이용해야 한다는 것을 알 수 있었다.
하지만 첫 접근이 많이 어려웠다. 내가 고민했던 지점들을 작성해 보고자 한다.
1. 섬의 경계를 어떻게 잡을 것인가?
섬이 여러개인만큼 각각의 섬을 구분할 수 있어야 한다.
2. 섬의 출발점을 어느 곳으로 잡아 최단거리를 구해야 하는가?
=> 섬은 언제 어디에서든 출발할 수 있는 위치를 가지고 있다. 그렇기 때문에 어느 출발점을 잡아야 최단거리로 만들 수 있는지가 어려웠다.
인터넷에 다른 분들이 어떻게 풀었는지 찾아보면서 감을 잡아야겠다는 생각에 이것저것 찾아봤다.. 역시 골드 이상 문제는 아직은 많이 어렵게 느껴지는 것 같다.
결론적으로 내가 고민했던 지점 두군데에서 각각 DFS, BFS를 사용하여 풀어야 하는 문제였다. 두번 쓴다니! 조금 생소했지만 DFS와 BFS를 복합해서 쓸 수 도 있고, 똑같은 유형을 두 번 겹쳐 사용할 수 있다는 점을 항상 유념해두고 문제풀이 시 주의해야겠다고 생각했다.
👨💻 코드 작성
섬을 구분하기 위해서는 라벨링이 꼭 필요하다고 생각했다.
2번 섬, 3번 섬, 4번 섬.. 이런 식으로.
이것을 DFS로 먼저 표현해보자.
global count
count = 2
def dfs(x, y):
if x <= -1 or x >= N or y <= -1 or y >= N:
return False
if graph[x][y] == 1:
graph[x][y] = count
dfs(x-1, y)
dfs(x, y-1)
dfs(x+1, y)
dfs(x, y+1)
return True
for i in range(N):
for j in range(N):
if dfs(i, j) == True:
count = count + 1따단~ 이렇게 dfs를 이용하여 현재 섬들의 상태를 라벨링해줄 수 있다.
이제 가장 관건인 최단거리를 구해보도록 하자.
당연히 최단거리를 구하는 것이므로 BFS를 이용하도록 한다.
항상 BFS와 DFS는 내가 아는 공식에서 조금만 생각을 전환해보면 된다는 것을 기억하고 있자!
def bfs(n):
global answer
visited = [[-1] * N for _ in range(N)]
queue = deque()
for i in range(N):
for j in range(N):
if graph[i][j] == n: #만약 있는 곳이 섬이라면
queue.append((i, j)) #섬의 위치 저장
visited[i][j] = -1 #방문처리
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + xt[i]
ny = y + yt[i]
if nx < 0 or nx >= N or ny < 0 or ny >= N:
continue
if graph[nx][ny] > 0 and graph[nx][ny] != n:
answer = min(answer, visited[x][y])
if graph[nx][ny] == 0 and visited[x][y] == -1:
visited[nx][ny] = visited[x][y] + 1
queue.append((nx, ny))visited 방문 배열을 bfs 함수를 불러올때마다 초기화해줘서 모든 섬에 대하여 최단거리를 체크할 수 있게 해준다. 당연히 bfs이므로 queue를 이용할 것이고, 만약 방문한 곳이 섬이라면 거리를 체크해야 하는 위치로 저장을 해 준다.
일단 초기값으로 섬의 위치들을 queue에 저장을 해 주고, 섬위 위치에서 상하좌우로 이동한다. 만약 이동한 값이 다른 섬이라면 현재 visited 배열에 저장된 그 전까지의 거리와 그 전에 존재했던 정답 둘 중에 작은 것을 선택해야 한다.
만약 아직 바다에 존재하거나 아직 방문하지 않은 곳을 마주했다면, visited 의 값을 하나 늘리고, 거리를 체크해야 할 곳으로 선정해준다.
이렇게 그래프에 대하여 BFS/DFS에 대한 감을 잊지 않도록 해야 한다. 이차원도 어렵지만 공부를 꼭 열심히 해야 하느니라..