문제 링크
https://www.acmicpc.net/problem/1002
풀이 전 계획과 생각
이 문제를 요약하면 다음과 같다.
(x1,y1)과 (y1, y2)가 주어지고 좌표 1에서 계산한 길이 r1과 좌표 2에서 계산한 길이 r2가 주어졌을 때 타겟이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오. 단 좌표의 수가 무한대라면 -1 출력
처음 이 문제를 보았을 때 아무것도 생각이 나지 않아서 별 생각을 다 해 보았다. 좌표가 '정수'로 되어 있으니까 해당 범위에 존재할 수 있는 모든 정수를 찾으란 말인가? 예를 들어 범위가 0에서 1이면 0.1, 0.2는 좌표가 아니니까 0,1 두 개만 있고 그런 거? 컴퓨터그래픽스에 나오는 원에 점찍기 알고리즘 같은 건가? 물론 아니었다.
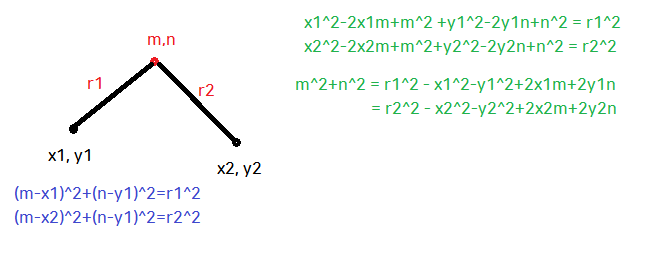
윈도우즈 그림판에 그림을 그려놓고 별 쓸데없는 계산을 하고 있는 모습을 볼 수 있다.
그러다가 저 삼각형을 가만히 보고 있다가 생각이 떠올랐다.
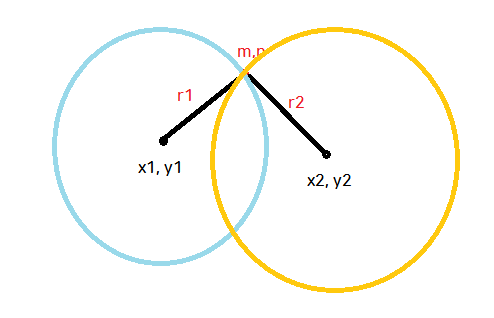
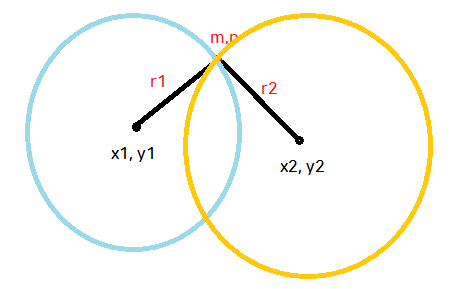
즉, 이것은 반지름이 각 r1, r2인 두 원의 중첩 여부에 대한 문제였던 것이다.
다시 말해서 중첩되지 않으면 0(길이를 쟀는데 틀릴 수 있단 말인가? 문제가 모순 아냐? ㅋㅋㅋ), 한 점에서만 만나면 1, 두 점에서 겹치면 2가 된다.
그래서 저 그림을 그대로 코드로 구현해 보았다.
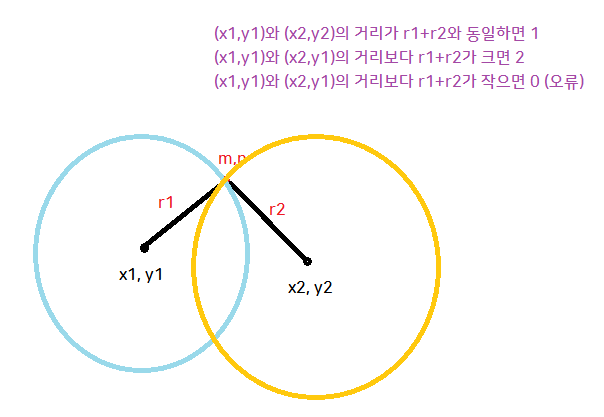
물론... 원의 중첩은 저게 전부가 아니다. 예시 입력과 출력을 넣어보니 잘 출력이 돼서 그대로 실행시켰더니 재빠르게 '틀렸습니다'가 떴다. ㅠㅠ 그것은 나중에 다시 조사해 보았다...
내가 수학을 언제 공부해 봤더라... 대학교 경제학입문까지 합쳐도 거의 지난 세기의 일이 아닐까? ㅋㅋㅋ 그래서 다 까먹고 있다가 막연히 의식의 흐름대로 했더니 잠시 혼란이 있었다.
풀이
그래서 원의 중첩에 대해 열심히 구글을 통해 공부해 보고 제출한 정답은 이렇게 되었다.
counter=int(input(""))
table=[]
for i in range(counter):
xyr=input("").split()
# 0 0 3 0 7 4: (0-0)**2+(0-7)**2
# 0 1 2 3 4 5
table.append(xyr) # x1, y1, r1, x2, y2, r2
for element in table:
#print((int(element[0])-int(element[3]))**2+(int(element[1])-int(element[4]))**2,(int(element[2])+int(element[5]))**2)
x1=int(element[0])
y1=int(element[1])
r1=int(element[2])
x2=int(element[3])
y2=int(element[4])
r2=int(element[5])
if x1==x2 and y1==y2:
if r1==r2:
print(-1)
else:
print(0)
# 거리가 |r1-r2|보다는 크고 r1+r2보다는 작아야 한다
elif (x1-x2)**2+(y1-y2)**2==(r1+r2)**2 or (x1-x2)**2+(y1-y2)**2==(r1-r2)**2:
print(1)
elif (x1-x2)**2+(y1-y2)**2<(r1+r2)**2 and (x1-x2)**2+(y1-y2)**2>(r1-r2)**2:
print(2)
else:
print(0)
# r1, r2의 조합이 불가능한 조합인 경우
# (x1,x2), (y1, y2)의 거리보다 r1+r2가 큰 경우
# (x1,x2)와 (y1, y2)가 동일한 경우:
# r1과 y2가 동일한 경우: 무한대
# 다른 경우: 0풀이하면서 막혔던 점과 고민
첫째, 파이썬에서 제곱은 **인데 자꾸 ^를 입력해서 자꾸 혼란에 빠졌다.
둘째, 예제에 나온 마지막 입력문이 1 1 1 1 1 5인데 당연히 (x1,y1)과 (x2, y2)가 동일한 사례인 것을 간과하고 '어? 좌표 거리보다 반지름의 합이 더 큰데 왜 2가 아니고 0이지?'만 한참 생각했다. ㅋㅋㅋ
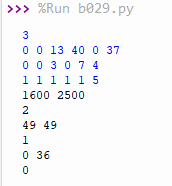
두 좌표가 동일하면 r1과 r2 또한 동일한 경우에 한하여 원 위의 모든 점이 해당하기 때문에 -1을 출력해야 하고 아닌 경우는 0을 출력해야 한다. (아무튼 문제에게 불만이 있다. 측정 자체가 틀려먹었다면 2나 1이나 -1이 출력된 경우도 모두 틀렸을 수 있는 것 아닌가? ㅋㅋ)
그래서 결국 두 좌표가 동일한 경우까지 조건문에 포함시켰는데도 합격이 안 되었다... 그래서 지금 수학을 처음부터 다시 공부할 건 아니니까 급히 원의 중첩의 조건에 대해서 검색을 해보았다.
물론 나 빼고 모든 사람이 다 알고 있는 사실이겠지만 원의 중첩은 이런 그림만 있는 게 아니다.
아래와 같은 경우가 있다는 걸 깜빡했다.

그래서 생각보다 쉬웠지만 그렇다고 너무 자신만만하게 감 닿는 대로(!) 입력했더니 불합격이 떴던 험난한 테스트였다.
풀이 후 알게 된 개념과 소감
자꾸 까먹는데 파이썬에서 제곱은 ^이 아니라 **였고...
원의 중첩에 대해서 상기해보는 유익한 시간이었다. 중학교 몇 학년 때 나오는 거더라? ㅠㅠ
그래도 원의 중첩에 대해서 조사해 본 다음에는 막힘없이 합격해서 뿌듯하다.
