백준 온라인 저지 1697번: 숨바꼭질

솔직히 내가 아직 전혀 이해하지 못하고 있는 분야가(딴 건 아냐!!! ㅋㅋㅋ) BFS이다.

그래서 다른 BFS 문제를 먼저 풀어보려고 했을 땐 마치 바퀴를 처음부터 발명하려는 사람처럼(...) 그래프에서 일일이 다음 노드를 찾아가는 과정을 리스트로 대충 구현하다가 시간초과 빨간 딱지를 잔뜩 얻어맞고 그대로 멘탈이 나가고 말았다. ㅋㅋㅋ

일단 전혀 이해를 못하고 있는 개념이니까 문제를 풀면서 이해해보겠다는 마음으로(문제를 혼자서 다 이해하는 건 아예 포기하고) 문제 해설부터 읽어본 다음에 코드를 그대로 베끼지 않고 스스로 구현해보기로 했다.

문제 링크

https://www.acmicpc.net/problem/1697

풀이 계획

이 문제는 이렇게 구성되어 있다.

출발점의 위치가 N, 도착점의 위치가 K이다.
1초 동안 이동할 수 있는 거리는 세 가지가 있다.

• 현재 위치에서 -1
• 현재 위치에서 +1
• 순간 이동: 현재 좌표의 2배
  여기에서 필요한 경우의 수들의 최단 거리를 모두 계산하여 도착점까지 갈 수 있는 최단 시간을 측정하는 것이다.

여기저기 검색해본 결과 이것을 푸는 가장 기본적인 방법은 이렇게 구성된다.

• 앞으로 계산할 출발점 목록을 관리하는 리스트와 좌표별 최단 시간을 관리하는 리스트를 만든다.
• 계산할 현재 출발점을 빈 리스트에 하나씩 넣는다.
• (1) 만약에 현재 출발점의 값이 K(도착점)와 일치한다면 더 이상 계산할 필요가 없으니 현재 출발점까지의 최단거리를 출력하고 종료한다. 여기에 해당하지 않는다면...
• 현재 출발점에서 1초만에 갈 수 있는 좌표는 세 가지이다.
  • 현재 출발점-1
  • 현재 출발점+1
  • 현재 출발점x2
• 위 세 가지 좌표의 현재 최단 시간은 현재 출발점의 최단 시간+1이다. 이것을 좌표별 최단 시간 목록에 업데이트해준다. 그리고 이 좌표들을 다음 출발점 목록에 추가한다. 아래의 경우만 제외하고.
  • 단, 만약에 그전 출발점에서 최단거리 측정을 한 기록이 이미 존재하는 좌표라면, 그때 계산한 값이 훨씬 적을 것이기 때문에 업데이트하지 않는다. 그리고 다음 출발점 목록에도 중복될 것이기 때문에 넣지 않는다.
  • 현재 출발점x2의 값이 도착점보다 터무니없이 큰 경우에도 이 값은 계산에서 제외한다. 예를 들어 N과 K는 모두 10만 이하인데 현재 좌표가 9만이고 목표 도착점이 10만이라면 현재 출발점x2를 한 18만에서 현재 출발점-1을 8만 번 해서 8만1초 만에 가는 것보다는 현재 출발점+1을 1만 번 해서 1만 초 만에 가는 것이 훨씬 빠르다는 것이 자명하다. 그러니까 18만까지 가는 최단 거리와 18만1, 17만9999, 36만까지 오는 최단 거리는 고려할 필요가 없다. 이런 경우에는 다음에 계산할 좌표를 무한히 3개씩 늘릴 필요가 없다.
  • 그리고 만약에 세 가지 다음 좌표 중 하나가 도착점 K와 같다면? 그냥 현재 좌표의 최단 시간에서 +1을 더한 값을 출력하고 이대로 종료하면 된다. 이것을 하지 않고 그냥 계산해서 좌표에 저장만 하는 것을 반복한다면 이 값이 현재 좌표로 돌아와서 그것이 도착점과 일치해서 앞의 (1)에서 반복문을 종료하게 될 때까지 시간이 너무 오래 걸린다.
• 이렇게 업데이트된 다음 출발점에 대하여 현재 출발점이 목표점과 동일해질 때까지 계산을 반복한 뒤에 해당 좌표의 현재 최단 거리를 출력한다.

이렇게 푼다는 것을 완전히 스스로 알아냈다면 참 좋겠지만 지금 BFS를 아예 모르기 때문에 그럴 수는 없었다는 점은 아쉽고... 어쨌든 공부를 해서 BFS를 활용하는 방법을 잘 알게 되도록 노력하는 계기로 삼도록 해야겠다.

풀이

import sys
N,K=map(int,sys.stdin.readline().split())
if N>K:
    print(N-K)
else:
    seconds=[0]*(133335+1)
    to_check = [N]
    while to_check!=[]:
        early_break=0
        current=to_check.pop(0)
        if current==K:
            print(seconds[current])
            break
        else:
            if current*2-K+1 > K-current:
                next_checkpoints=[current-1,current+1]
            else:
                next_checkpoints=[current-1,current+1,2*current]
            
            for element in next_checkpoints:
                if element==K:
                    early_break=1
                    break

                elif element>=0 and element<=133335 and seconds[element]==0 and element!=N:
                    seconds[element]=seconds[current]+1
                    to_check.append(element)
            if early_break==1:
                print(seconds[current]+1)
                break
            

풀이하면서 막혔던 점과 고민

혹시 또 시간 초과나 오류가 발생할까 봐 질문게시판에서 반례도 검색해보고 다른 사람들의 고민을 찾아보았는데 역시 좌표별 최단 시간을 모두 입력할 큰 배열을 만들고 그 배열을 모두 채워넣는 과정 때문에 시간초과가 뜰 것에 대해 많은 분들이 우려하고 있었다.

• 우선 N과 K는 10만 이하의 모든 자연수가 될 수 있다. 그러니까 출발점인 N이 K보다 클 수도 있다는 것이다. '순간 이동'은 양의 2배로만 갈 수 있으니까 N이 K보다 크면 이동 방법은 -1밖에 없으니 최단 시간은 K-N으로 확정된다.
• 계산 중에 현재 출발점이 이미 엄청나게 커졌을 때는 어떨까?

# 75000에서 150000으로 갔다가 100000으로 돌아오기: 50001초, 직진 25000초 
# 60000에서 120000으로 갔다가 100000으로 돌아오기: 20001초, 직진 40000초
# 70000에서 140000으로 갔다가 100000으로 돌아오기: 40001초, 직진 30000초

대충 이렇게 주먹구구식으로 계산해 보니 도착점이 최댓값 10만인 경우에 약 7만 근처부터는 x2를 했다가 -1로 되돌아오는 것이 +1로 계속 직진하는 것보다 절대로 빠를 수 없게 된다. 그러니까 출발점 좌표는 약 140000 부터는 예상 최단거리와 무관하기 때문에 빼도 된다.

정확한 값을 계산해 보았다.

for a in range(50000,70000):
    if 100000-a < a*2-100000+1:
        print("현재 위치가",a,"일 때",a*2, "로 순간이동 후 돌아오려면",a*2-100000+1,"직진하면",100000-a)
        break

결과는 이렇게 나왔다.

현재 위치가 66667 일 때 133334 로 순간이동 후 돌아오려면 33335 직진하면 33333

따라서 현재 위치가 66666일 때까지는 x2를 했다가 -1을 하는 게 +1을 33334번 하는 것보다 10만까지 더 빨리 올 수 있지만 66667부터는 아니기 때문에 66667x2=133334부터는 다음 최단거리를 계산할 필요가 없다.

따라서 길이가 133335인(마지막 좌표가 [133334]인)리스트를 좌표별 최단거리 저장에 사용하고 이 리스트에 들어오지 않는 더 큰 좌표는 무시하기로 했다.

이렇게 해서 처음에 검색해서 알아봤던 힌트보다 스스로 문제에 대해 많은 점을 생각해보고 스스로 시간복잡도와 공간복잡도를 줄여보는 시간을 가져보았다.

그런데 왜 이렇게 거의 모든(?) 경우의 수를 다 넣어보는 것을 너비우선탐색(BFS)이라고 할까?
아마도 시작점이 5, 도착점이 17인 위 문제의 예시 문제를 놓고 탐색하는 과정을 살펴보면 이런 모양이 되기 때문인 것 같기도 하다.

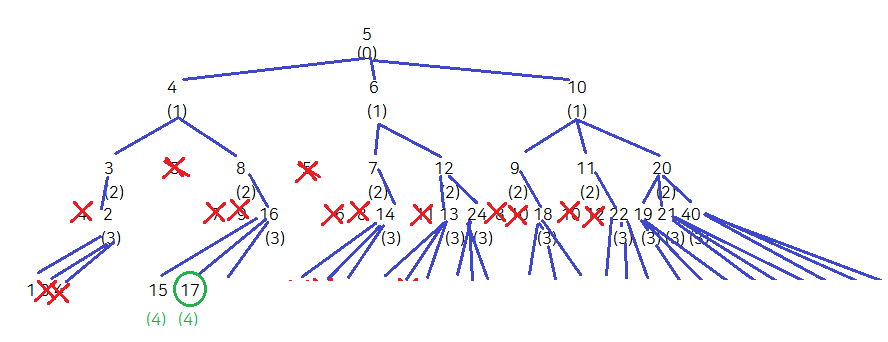
그림상으로 보면 17을 찾을 때까지 너비 우선 탐색을 하고 있는 게 맞긴 맞는 것 같다. 아니면 말고... ㅋㅋㅋ

소감

너무나 생소한 개념인 BFS를 나름대로 검색해가면서 열심히 공부해서 시간복잡도와 공간복잡도를 계속 줄여나가는 보람찬 시간이었다.