백준 2579번 계단 오르기
문제 링크
https://www.acmicpc.net/problem/2579
풀이 전 계획과 생각
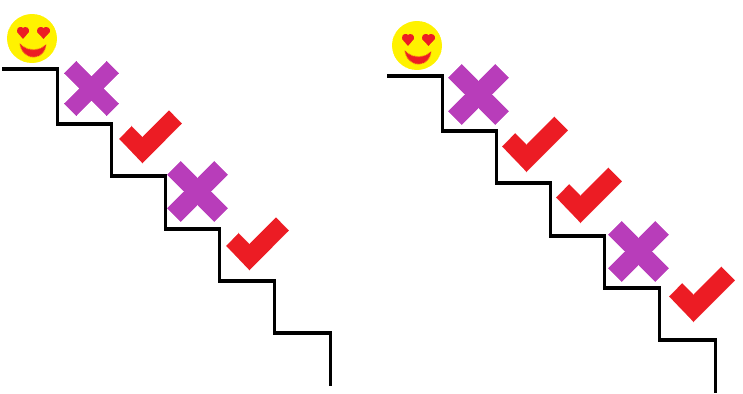
처음에는 이 문제가 굉장히 어렵게 느껴졌다. 앞에서 푼 1149번 RGB거리에서는 현재 색상 선택은 직전 색상과만 다르면 되는데 이번에는 계단을 '세 번 연속'으로 밟으면 안 된다는 점에서 어디까지 고려해야 하는지 상상이 잘 되지 않았다.
마지막 계단은 반드시 밟아야 한다고 했으니까, 현재 계단을 밟고 득점하려면 조건이 뭐가 있지? 직전 계단을 밟았다면 전전 계단은 밟으면 안 되고, 직전 계단을 안 밟고 전전 계단을 밟았다면 전전전 계단은 밟아도 되는데 전전전과 전전전전을 동시에 밟으면 안 되고...
그래서 각각의 계단을 밟을 때의 조건을 처음부터 일일이 생각해보았다.
# 첫번째 계단 최댓값: 첫번째 계단
# 두번째 계단 최댓값: 첫번째 계단+두번째 계단 (각 계단의 점수는 모두 양수이기 때문에 두번째 계단만 밟으면 당연히 최댓값 안 나옴)
# 세번째 계단 최댓값: 1+2+3은 안 되니까 2+3과 1+3 중 최댓값
# 세번째 계단 + max(첫번째 계단 최댓값, 두번째 계단 최댓값)
# 네번째 계단 최댓값:
# 2+3+4는 안 되니까 1+3+4나 1+2+4 중 최댓값
# 다섯번째 계단 최댓값:
# 3+4+5나 2+3+4나 1+2+3이 섞여있으면 안 됨
# 1+2+4+5, 1+3+5, 2+3+5, 2+4+5 중 최댓값
# 그 위의 계단
# 현재계단+직전계단+전전전총점, 현재계단+전전계단+전전전계단+전전전전전총점,
# 현재계단+전전계단+전전전전총점
저것을 더 줄일 수 있다는 것은 나중에 이 포스팅을 쓰려고 정리하면서 뒤늦게 깨달았고... 일단 저 조건을 모두 때려박은 코드를 제출했더니 너무 쉽게 합격이 떴다.
그런데 정말 i-5까지 계산해야만 할까? 이 문제는 이 포스팅을 쓸 때 뒤늦게 아이디어가 떠올라서 해결되었다.
풀이 (코드 블록 첨부)
# 백준 2579번 계단 오르기 수정
import sys
def stairs(n,scores,scores_total):
current_max = scores[0]
if n==1:
return current_max
scores_total[0]=current_max
current_max = scores[0]+scores[1]
if n==2:
return current_max
scores_total[1]=current_max
current_max=scores[2]+max(scores[1],scores_total[0])
if n==3:
return current_max
scores_total[2]=current_max
for i in range(3,n):
scores_total[i] = scores[i]+max(scores[i-1]+scores_total[i-3],scores_total[i-2])
return scores_total[n-1]
N = int(sys.stdin.readline())
scores_arr=[int(sys.stdin.readline()) for x in range(N)]
#print(scores)
#scores_total_arr = [0 for x in range(max(5,N))]
scores_total_arr = [0 for x in range(N)]
print(stairs(N,scores_arr,scores_total_arr))
#print(scores_total)
풀이하면서 막혔던 점과 고민
포스팅을 쓰려고 아이디어를 다시 정리해 보다가 이런 생각이 떠올랐다.
직전 계단을 밟았다면 전전 계단은 3연속이 되니까 당연히 밟으면 안 된다. 그런데 전전전 계단부터는 따질 필요가 없다. 전전전 계단과 전전전전 계단을 밟아도 되고 전전전 계단과 전전전전전 계단을 밟아도 되는데 어차피 전전 계단을 안 밟았으니까 전전전 계단을 밟는 모든 조건이 허용된다.
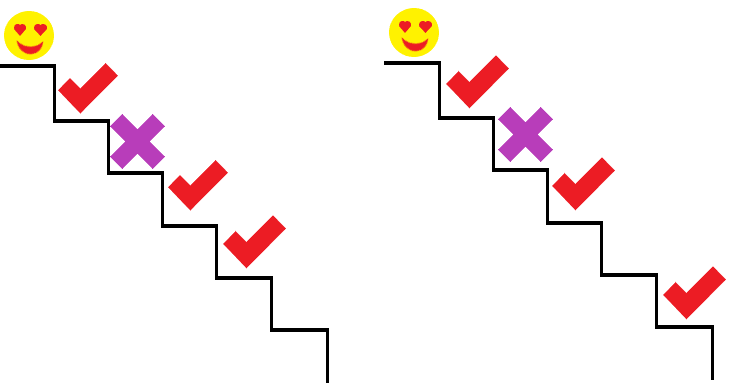
한편 직전 계단을 안 밟았다면 두 칸을 뛰어넘을 수는 없으니까 전전 계단을 밟아야 한다. 그런데 전전 계단을 밟는 경우에도 전전전 계단을 밟고 전전전전 계단을 안 밟아도 되고 전전전 계단을 안 밟고 전전전전 계단을 밟아도 된다. 이 조건도 전전계단을 밟는 조건 자체에 포함되기 때문에 i-3이나 i-4에 대해 별도로 연산을 할 필요가 없다.
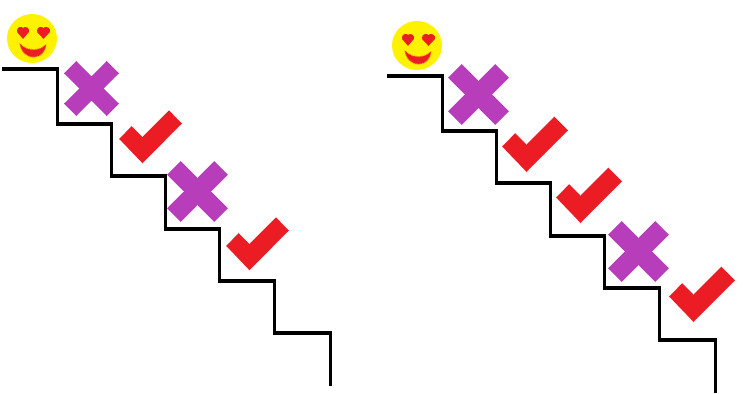
그러니까 위에서 구상한 조건은 다음과 같이 간소화할 수 있다.
# 첫번째 계단 총점: 첫번째 계단
# 두번째 계단 총점: 첫번째 계단+두번째 계단 (각 계단의 점수는 모두 양수이기 때문에 두번째 계단만 밟으면 당연히 최댓값 안 나옴)
# 세번째 계단 최댓값: 세번째 계단 점수 + max(두번째 계단 단독점수, 첫번째 계단 총점)
# 네번째 계단 최댓값:
# 2+3+4는 안 되니까 1+3+4나 1+2+4 중 최댓값이라고 했는데
# 이것은 네번째 계단 점수 + max(세번째 계단 점수+첫번째 계단 총점, 두번째 계단 총점)과 동일하다. 여기서부터 max 함수 안에 넣을 덧셈 연산이 동일해지니까 반복문을 시작할 수 있다.
# 다섯번째 계단 최댓값:
# 3+4+5나 2+3+4나 1+2+3이 섞여있으면 안 됨
# 1+2+4+5, 1+3+5, 2+3+5, 2+4+5 중 최댓값
# 이 말은 다시 수정하면 다섯번째 계단 점수 + max(네번째 계단 점수+두번째 계단 총점(당연하게도 1+2+4+5보다 2+4+5는 작은데 왜 이걸 비교했지? ㅋㅋㅋ), 세번째 계단 총점(그것이 1+3인지 2+3인지는 세번째 계단에서 이미 판단이 끝났다))
# 그 위의 계단
# 현재계단+max(직전계단+전전전총점, 전전계단총점)
# 전전계단에서 전전전계단을 밟고 전전전전전계단을 밟을지 아니면 전전계단에서 전전전전계단을 밟을지는 전전계단의 조건에 이미 포함되어 있다
풀이 후 알게된 개념과 소감
코드를 많이 수정했는데 시간은 별 차이가 나지 않았다. 애초에 별로 어렵지 않은 문제라서 그런 것 같다.
아무튼 처음으로 아무데도 검색을 안 해보고 완전히 혼자서 생각해서 풀었는데 어려움 없이 합격해서 뿌듯하다.
