백준 9461번 파도반 수열
문제 링크
https://www.acmicpc.net/problem/9461
풀이 전 계획과 생각
지난 주에 BFS와 DFS 관련 문제풀이가 너무 어려웠기 때문에 과연 이번 주에도 공부를 계속할 수 있을지 자신감이 바닥을 찍은 상태에서 문제를 살펴보았다.

파도반 수열(padovan sequence)은 다음과 같이 연결된 삼각형들 중에서 N번째의 정삼각형의 길이를 나타낸다.
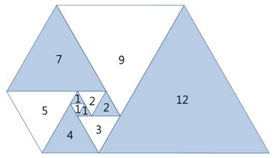
그리고 좀 찾아봤더니
P(1)=1
P(2)=1
P(3)=1
N>3인 경우 P(N) = P(N-3)+P(N-2)
라는 규칙이 있었다.
그래서 처음에는 그냥 아무 생각 없이 recursion을 했고... ㅋㅋㅋ
def padovan0(n):
if n==1:
return 1
elif n==2:
return 1
elif n==3:
return 1
else:
return padovan0(n-2)+padovan0(n-3)결과는 당연히도 시간초과였다 ㅋㅋㅋ
이게 왜 동적 프로그래밍 문제냐면 작은 문제의 결과를 바탕으로 큰 문제를 계속 풀어나가는 것이기 때문이다.
이 문제의 입력 형식을 다시 살펴보자.
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
N에서 1까지 줄어드는 과정을 일일이 처음부터 다시 계산할 필요가 없다. 파도반 수열은 하나이기 때문에 T개의 N값들 중에서 가장 큰 값까지의 결과를 미리 다 구해놓고 그 테이블에서 다시 뽑아오면 된다.
그러니까 저 입력값이 만약에
3
98
99
100이렇다면 98에 대하여 97,96,95,...1까지 다 구하고 또 99에 대하여 98,97,96...1까지 또 다 구하고 또 100에 대하여 99,98,97...1까지 다시 계산할 필요는 당연히 없고,
98에 대하여 1,2,3,...98까지 구한 뒤에
또 99에 대하여 1,2,3...99까지 또 구하고
마지막으로 100에 대하여 1,2,3,...100까지 다시 구할 필요도 없고
일단 100까지(배열에서 99번) 구한 다음에 table[97], table[98], table[99]를 호출하면 되는 것이었다.
풀이 (코드 블록 첨부)
import sys
T=int(sys.stdin.readline())
#print(T)
N = [int(sys.stdin.readline()) for x in range(T)]
#padovan_array = [0 for x in range(102)]
padovan_array = [0 for x in range(max(max(N),3))]
padovan_array[0]=1
padovan_array[1]=1
padovan_array[2]=1
for i in range(len(padovan_array)-3):
padovan_array[i+3]=padovan_array[i]+padovan_array[i+1]
#print(N)
for n in N:
print(padovan_array[n-1])풀이하면서 막혔던 점과 고민
동적 프로그래밍이 왜 동적 프로그래밍인지 깜빡해서 여러 개의 N값에 대해서 처음부터 다시 계산하는 코드를 만들었다가 뒤늦게 정신을 차렸(?)다. ㅋㅋㅋ
풀이 후 알게된 개념과 소감
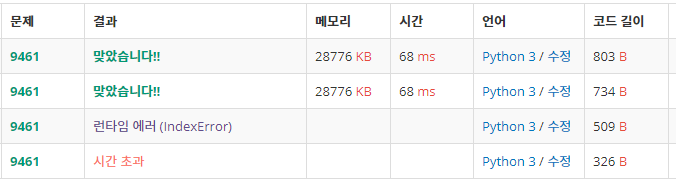
처음에는 recursion으로 해서 시간 초과,
다음에는 입력값마다 1부터 처음부터 다시 계산하는 반복문이 들어간 함수를 사용했더니 왠지 인덱스 에러가 뜸. (내가 100을 입력했을 땐 잘 되던데 왜? ㅋㅋㅋ 아무튼 매번 1부터 다시 계산하는 건 정상 실행되더라도 시간 초과가 당연히 뜰 것이다.)
마지막으로 1부터 100까지 미리 계산한 다음에 결과를 출력하는 것과 1부터 입력값 중 최댓값까지만 계산하는 것을 따로따로 제출해봤는데 메모리와 시간은 똑같이 떴다. 아마 채점 입력값에 100이 포함되기 때문에 실제 실행 과정이 동일한가보다.
이로써 동적 프로그래밍이 무엇인지 다시 생각해보는 계기가 되었다. ㅋㅋㅋ
