[1. Matching and Exposed(free vertex)]
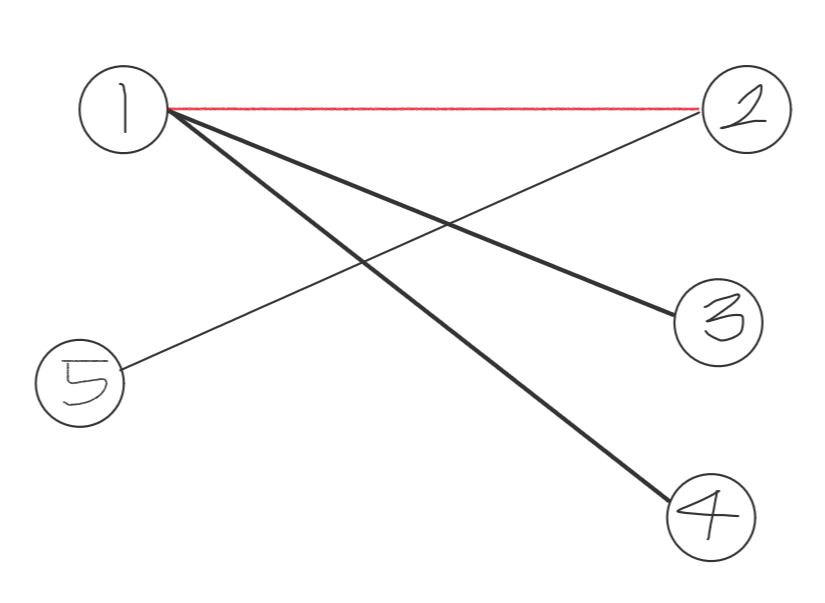
다음과 같은 무가중 그래프 G(V,E)가 주어졌을때 서로 매칭 된 Verex인 (1,2) 에 대해선 Matching이라고 하고 매칭되지 못한 Vertex(3,4,5)에 대해서 Exposed됐다고 합니다. 이때 Matching은 한개만 존재 할 수 있다.
[2. Alternating Path]
Alternating Path란 Matching에 포함된 Edge또는 Path와 Exposed에 속하는 Edge들이 교차할때 이러한 모든 간선들에 대해서 Alternating Path라고 한다. 예를들어 (1-2-5),(5-2-1-3) 에 해당하는 Path들도 Alternating Path이다.
[3. Augumenting Path]
Augementing Path는 Alternating Path들중 양끝 Vertex가 Exposed된 Path의 경우를 뜻합니다. 예를들어 다음 그래프에선 (1-2-5)의 경우는 Augmenting Path가 아닙니다. 왜냐하면 5 vertex만 Exposed하기 때문입니다. 하지만 (5-2-1-3)의 경우 Augumenting path입니다.
[3. 1 Why Augumenting Path is Important]
최대 이분 매칭(Bipartite matching)문제에 있어서 Augumenting Path는 중요한 정보를 담고 있습니다. 위의 그래프는 Matching Path가 1개만 존재한다. 하지만 방금 구한 Augmenting Path에서 기존의 Path를 차집합[symmetric difference] (A ⊕ B = (A ∪ B) − (A ∩ B))를 적용 시키게 되면 기존에 (1,2)를 끉어내고 (5,2)를 매칭시키고 (3,1)를 매칭시켜 다음과 같이 변하게 된다.
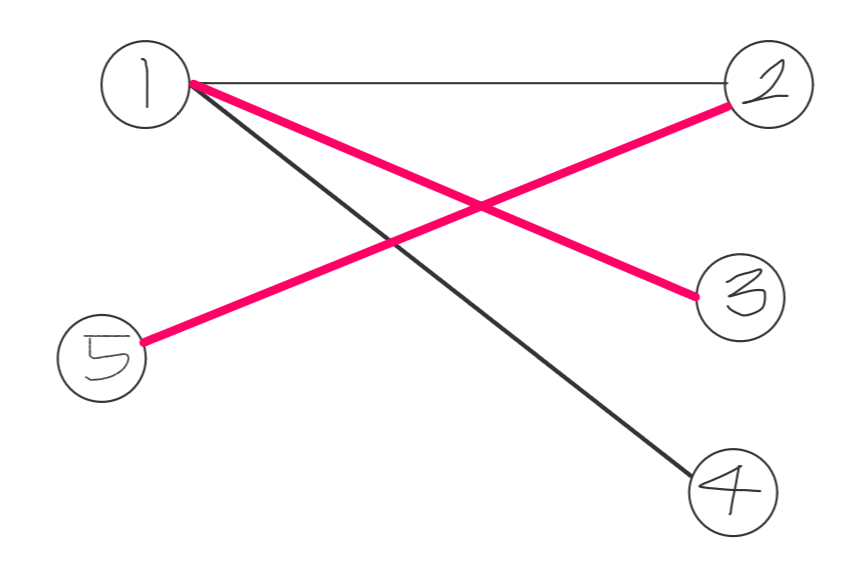
즉 다음정리를 만족하게 된다. M:현재 매칭그래프, P:Augumenting Path, | |는 매칭수, ⊕는 symmetric difference
|M ⊕ P| = |M| + 1
이를 바탕으로 다음 조건도 추론할 수 있게 된다.
|M ⊕ (P1 ∪ P2 ∪ . . . ∪ Pk)| = |M| + k
우리는 그래프에 존재하는 모든 Augumenting Path(P)정보를 찾아내서 symmetric difference를 적용시켜주면 최대 이분매칭을 발견할 수 있게 된다. 이는 필요충분조건을 만족한다. Augumenting Path가 존재하지 않는 그래프에서는 더이상의 이분매칭을 더 찾아 낼 수 없기 때문이다.
[3. 2 Bipartite Matching Using Augumenting]
우리는 이를 바탕으로 Bipartite Matching를 찾는 알고리즘을 생각해보면 다음과 같습니다.
- 최대매칭 그래프 M을 준비한다.(초기는 0)
- M에 대해 AugumentingPath가 없을때 까지 다음을 반복한다.(이때 Exposed to Exposed도 포함)
- M에 대한 P = (P1 ∪ P2 ∪ . . . ∪ Pk)들 중 길이가 가장 짧은 path P를 구한다.
- M<-M⊕P
- M = M ⊕ (P1 ∪ P2 ∪ . . . ∪ Pk)
참고자료: 1. https://gazelle-and-cs.tistory.com/35
2. http://www.columbia.edu/~cs2035/courses/ieor6614.S16/matching.pdf
