[문제이해]
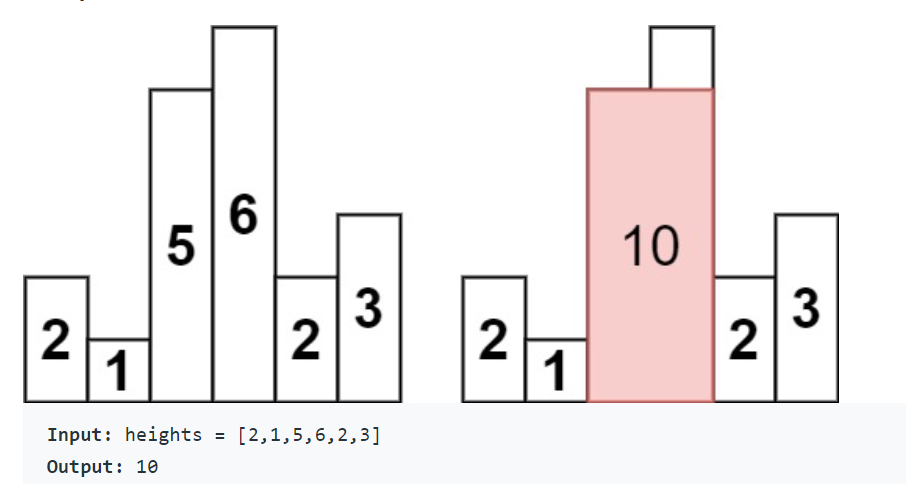
다음과 같이 높이가 주어졌을때 가장큰 직사각형의 넓이를 구하면 되는문제다.
이문제에 대해서 브루트포스하게 풀게 되면 O(N^2)이 발생하게 된다.
조건이 1 <= heights.length <= 10^5 이므로 시간초과가 발생하니 조금더 효율적으로 처리 할 필요가 있다.
[접근]
상황을 나눠서 정리해보자.
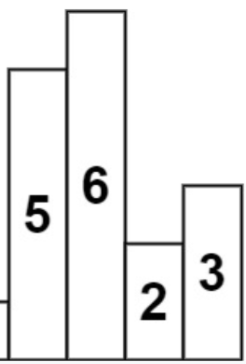
먼저 브루트포스 방식으로 접근하게 된다면 다음과 같다.
5부터 읽기 시작한다고 했을때 5를 시작점으로 5보다 크거나 같은 막대까지만 sequence하게 접근해서 넓이=5 X 2=10이다. 즉 5보다 작은 2와 3은 필요가 없게된다.
6인시점에서는 6 X 1=6이다.
2인 시점에서는 3이 2보다 크니 2X4=8이다. (5와6은 2보다 작으니)
3인 시점에서는 3X1=3이다.
즉 최대넓이는 10이 된다.
어떤 도형의 시점에서 그 높이를 가진 최대 사각형의 크기를 구하는데 있어 그것보다 작은 막대의 정보는 필요하지 않다.(
즉 이를 최대한 Memorization하는 방식으로 구해보자. 세가지 경우를 생각해보자.
현재 막대를 기준으로..
1. 이전 막대보다 큰막대가 나올경우
- 큰 막대 일경우 이전에 나온막대의 높이를 포함함과 동시에 계속 사용된다.
- 이전 막대보다 작을 경우
- 이전 막대 보다 작을경우 그 이전의 막대는 현재막대를 기준으로 높이는 사용되지 않는다. 그래서 이전 막대를 포함한 가장 넓은 사각형의 넓이를 구한후 컨테이너에서 제거 해준다.이때 제거할때 현재들어오는 포지션의 위치를 바꿔준다.(넓이 구하기 위해서)
- 이전 막대랑 같을 경우 그냥 넘어간다.
이를 바탕으로 이를 살펴보자
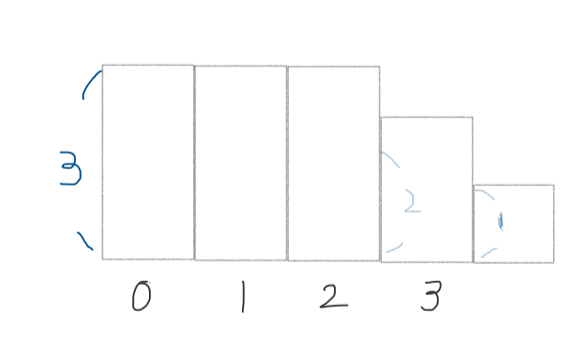
다음과 같은 높이의 히스토그램이 있을때 index별로 살펴보자.
index=0~2일경우
max_size=0(아직 계산안함)
stack=[{0(시작지점),3(높이)]
index=3일경우
index3인지점 보다 높이가 큰(높이 2보다 큰) 이전것들 다 제거하고 넓이 계산
max_size=9,
stack=[{0(시작지점),2(높이)]: 포지션위치를 제거 시점까지로 바꿔줬다.
index=4일경우
index4인지점 보다 높이가 큰 이전것들 다 제거하고 넓이 계산
2(이전 인덱스 높이)*(4(현재 인덱스위치)-0(이전 높이 의 시작 인덱스))=8이다. 즉 max_size인 9보다 작으므로 변하지 않는다.
stack=[{0(시작지점),1(높이)]: 포지션위치를 제거 시점까지로 바꿔줬다.
**다읽은후
컨테이너에 남은 것들을 전부 계산하고 max_size를 비교하고 제거한다.
stack[{0(시작지점),1(높이)}]을 처리해줘야한다.
(5(길이)-0(시작지점))X1(높이)=5이다
이떄 max_size인 9보다 작기에 변하지 않는다.
[구현]
#include <bits/stdc++.h>
using namespace std;
#define Pair pair<int, int>
#define pos first
#define height second
class Solution
{
public:
int largestRectangleArea(vector<int> &heights)
{
int __maxSize = 0, pos_length = heights.size();
stack<Pair> st;
for (int pos = 0; pos < pos_length; pos++)
{
int cur_height = heights[pos];
if (!st.empty() && cur_height == st.top().height)
continue;
else
{
int next_pos = pos;
while (!st.empty() && st.top().height > cur_height)
{
Pair next = st.top();
next_pos = next.pos;
st.pop();
// int before = st.empty() ? 0 : st.top().pos;
__maxSize = max(__maxSize, (pos - next_pos) * next.height);
}
if (!st.empty() && cur_height == st.top().height)
continue;
st.push({next_pos, cur_height});
}
}
while (!st.empty())
{
Pair next = st.top();
st.pop();
__maxSize = max(__maxSize, (pos_length - next.pos) * next.height);
}
return __maxSize;
}
};
int main()
{
vector<int> vec({2, 1, 5, 6, 2, 3});
vector<int> vec2({5, 4, 1, 2});
Solution *solution = new Solution();
cout << solution->largestRectangleArea(vec) << endl;
cout << solution->largestRectangleArea(vec2) << endl;
}