Maximum Bipartite Matching

[1.개념]

이분 매칭의 경우 각 시작점과 끝점이 1대1 매칭이 되야한다. 즉 Injective function(단사 함수)를 뜻한다. 다음상황을 보자

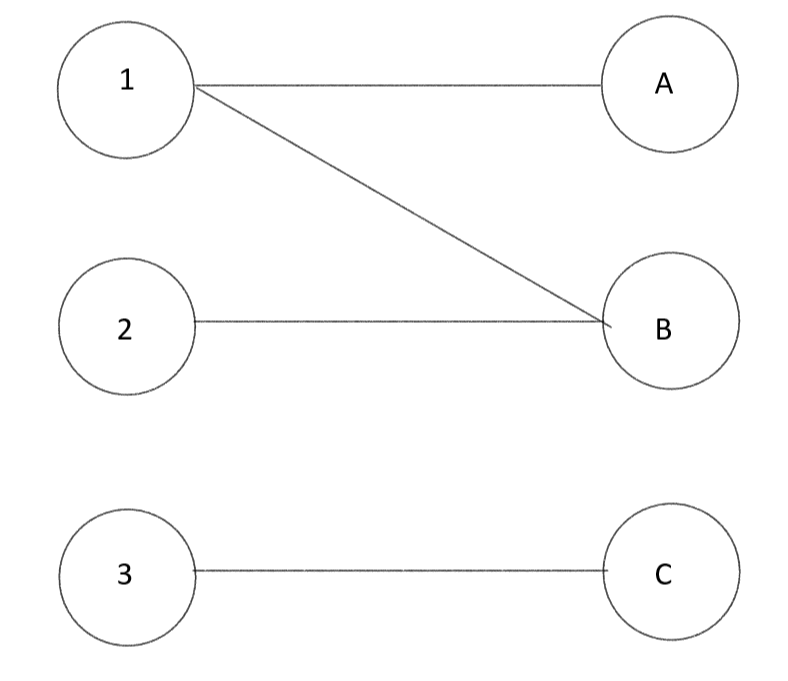
각 지원자가 있고(1~3), 지원가 원하는 직업들이(A~C) 있다. 이때 모든 지원자가 최대한 많은 직업과 1대1 매칭 될 수 있도록 해보자. 그렇다면 어떻게 해야할까? 이를 푸는 방법은 다양하다. 먼저 일반적인 브루트 포스 방식으로 완전탐색하게 되면 O(V*E^2)방식으로 풀 수 있다. 효율적인 방법으로 풀기 위해선 dfs방식으로 Matching하면 되는데 [일반적인 dfs]는 먼저 차례대로 매칭시키고 원하는 직업이 매칭 되어 있을경우 매칭되어 있는 지원자에게 부탁(재탐색)하는 방식으로 구현된다. 이런식으로 구현해도 O(V x E)로 구현가능하다. 하지만 이전시간에 공부한 [2.포드 풀커슨 알고리즘 방식] O(V x E)과 더 효율적인 방식인 [3.호프 카프 알고리즘 방식] O(√V x E)을 이용하여 구현해보자

[2. Ford Fulkerson Based approach for maximal Bipartite Matching]

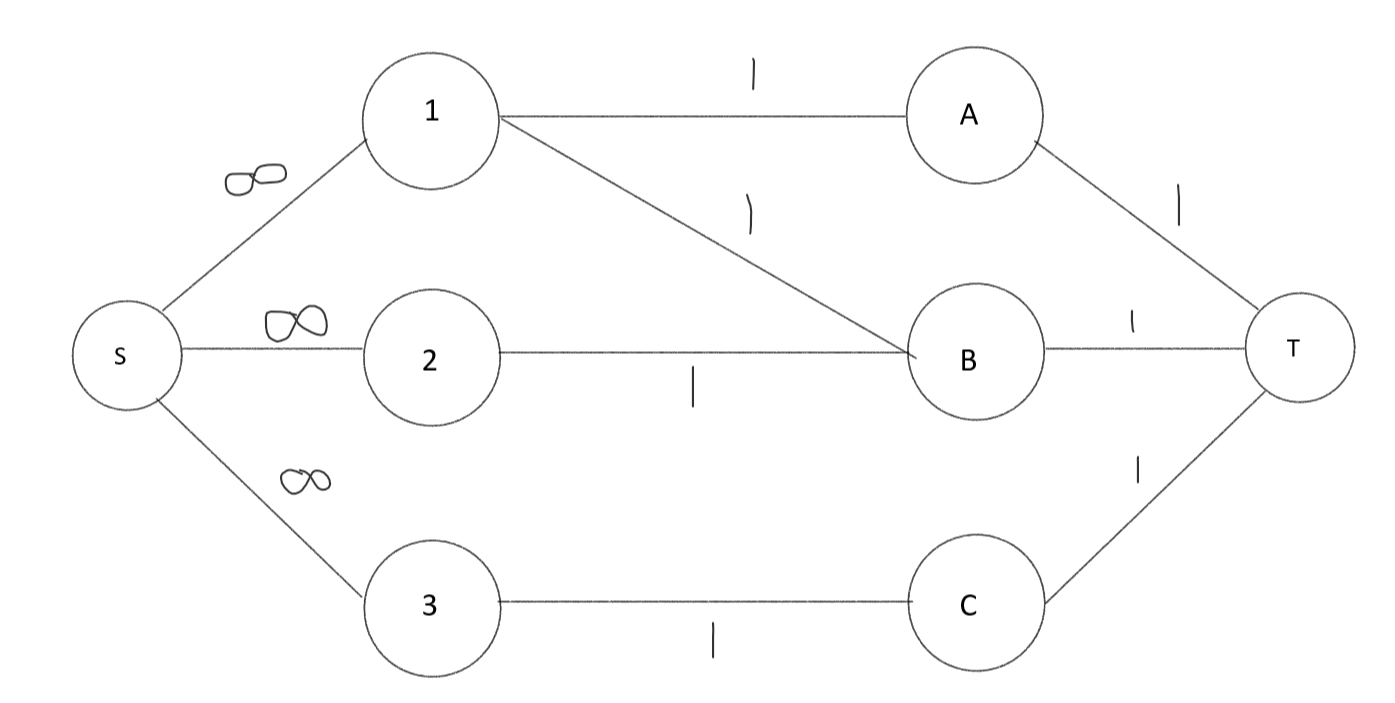
다음과 같이 그래프에 Sink와 Target을 정한후, sink에서 지원자A로 가는 edge weight=무한, 직업에서 Target으로의 edge weight은 1로 설정 하고 더이상 target으로 가는 residual graph가 없을때까지 dfs또는 bfs로 탐색하면 된다.

[3. Ford Fulkerson Based approach for maximal Bipartite Matching]