[자료구조] 우선순위 큐와 히프 (Priority Queue & Heap)

우선순위 큐(Priority Queue)란?

• 우선 순위의 개념을 큐에 도입한 자료구조
• 각 데이터들은 우선순위를 가지고 있다.
• 우선 순위가 높은 데이터가 먼저 나가게 된다.

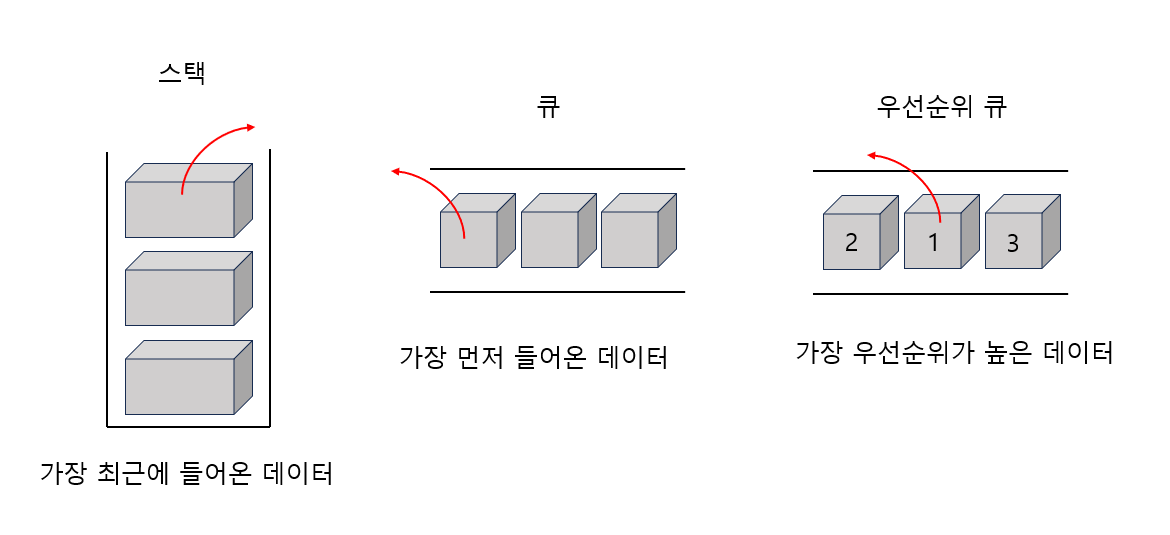
• 스택은 가장 마지막에 들어온 데이터가 나가는 LIFO(Last In First Out)
• 큐는 가장 먼저 들어온 데이터가 나가는 FIFO(First In First Out)
• 우선순위 큐는 가장 우선순위가 높은 데이터가 나간다.

최소 우선순위 큐

• 가장 우선 순위가 낮은 요소를 먼저 삭제

최대 우선순위 큐

• 가장 우선 순위가 높은 요소를 먼저 삭제

히프(Heap)란?

• 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
• 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조

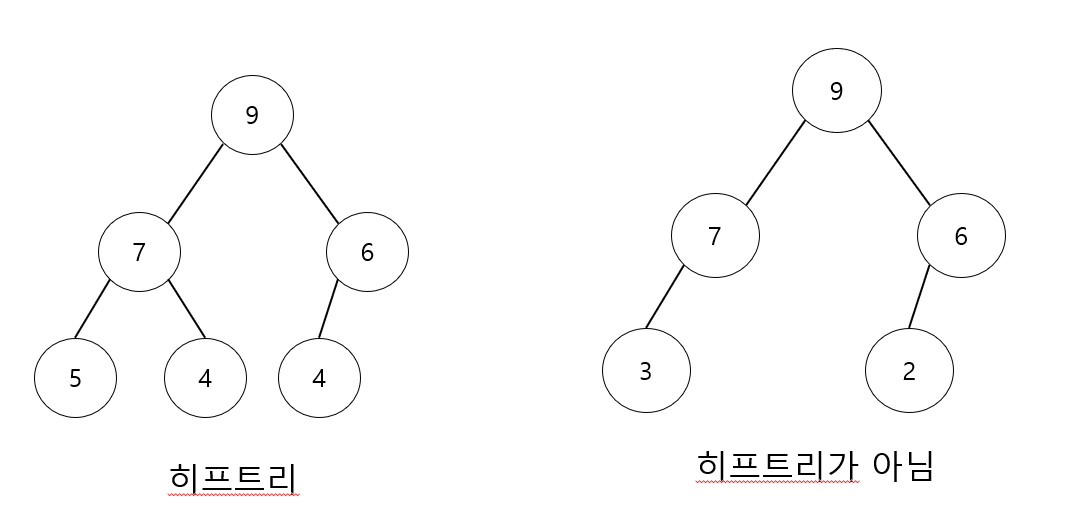
히프의 성질

• 완전 이진 트리 형태로 구성
• Key(부모노드) >= Key(자식노드)
  - 부모노드의 키값은 자식노드의 키값보다 크거나 같다.
• 중복된 값을 허용

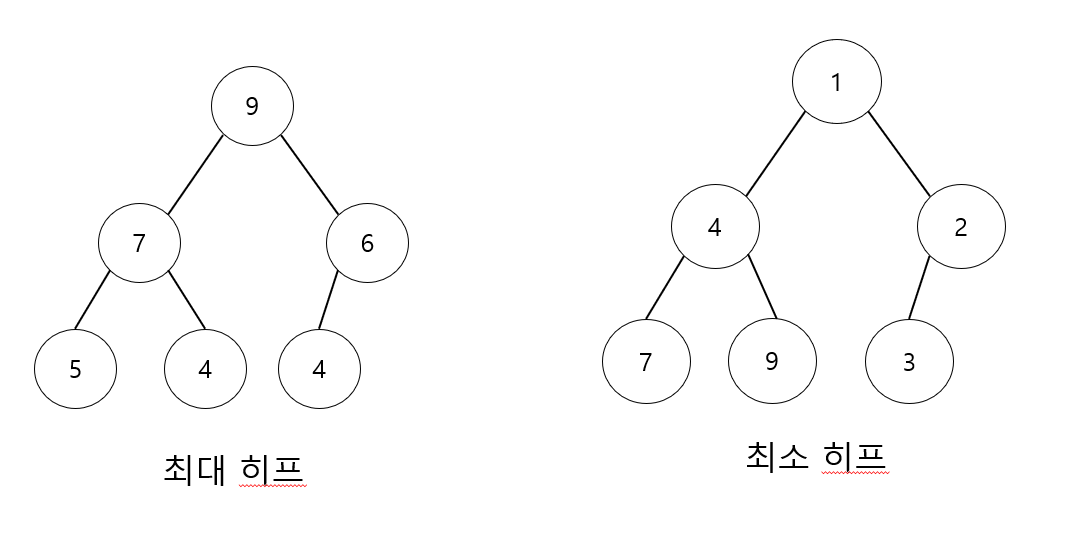
최대 히프(max heap)

• key(부모노드) >= key(자식노드)

최소 히프(min heap)

• key(부모노드) <= key(자식노드)

히프의 구현법

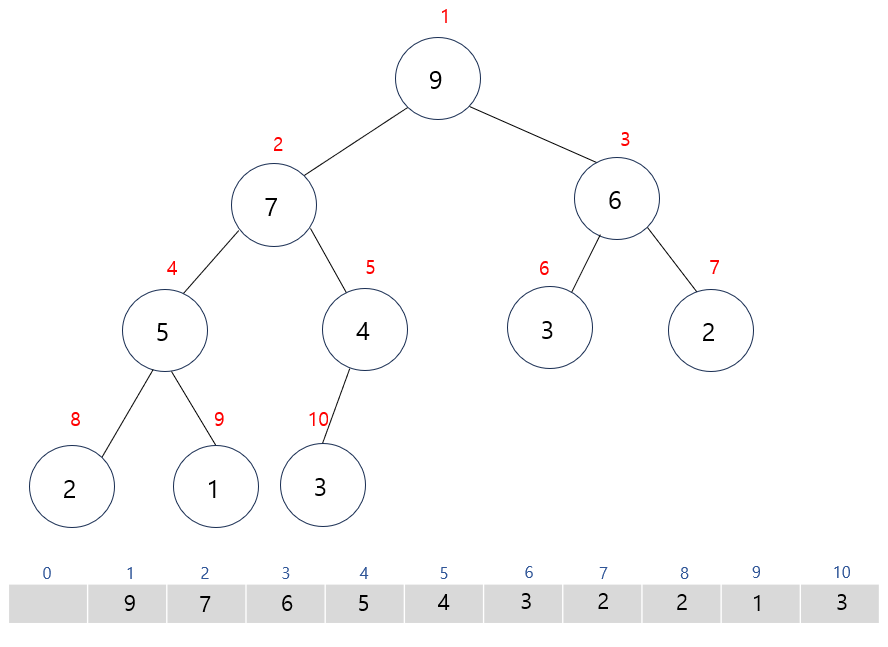
• 히프는 완전 이진 트리 구성으로 배열 형태로 구현됨
• 루트 노드부터 인덱스 1로 시작

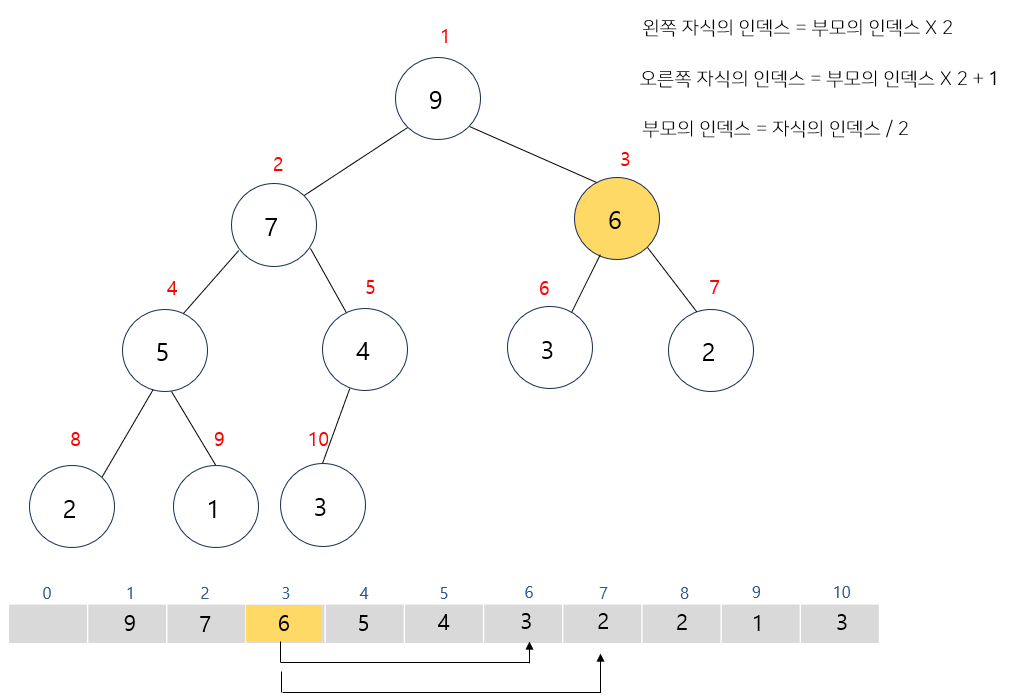
• 왼쪽 자식 인덱스를 알기 위해서는 부모의 인덱스 X 2
• 오른쪽 자식 인덱스를 알기 위해서는 (부모의 인덱스 X 2) + 1
• 부모의 인덱스를 알기 위해서는 자식의 인덱스 / 2

히프 삽입연산

• 새로운 노드를 히프의 마지막 노드로 삽입
• 새로운 노드를 부모 노드들과 교환

ex) 새로운 노드 8을 삽입

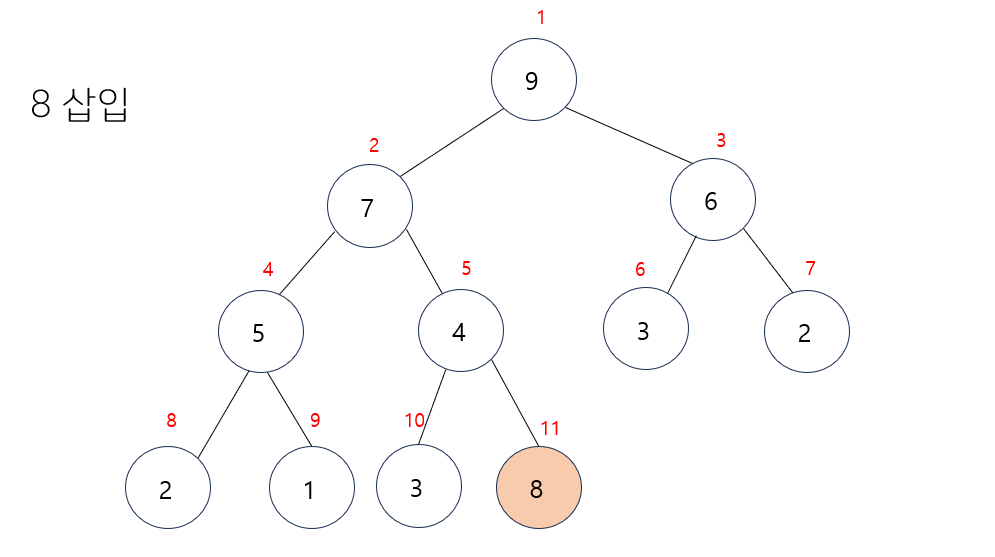
• 히프의 마지막 노드로 8을 삽입한다.

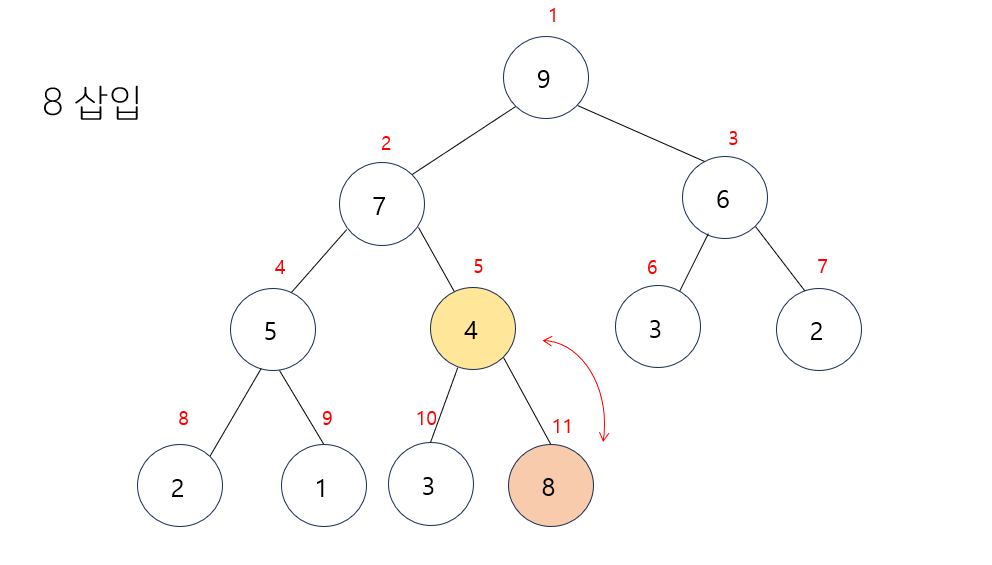
• 최대히프의 조건을 충족하기 위해 부모노드인 4와 비교를 한다.

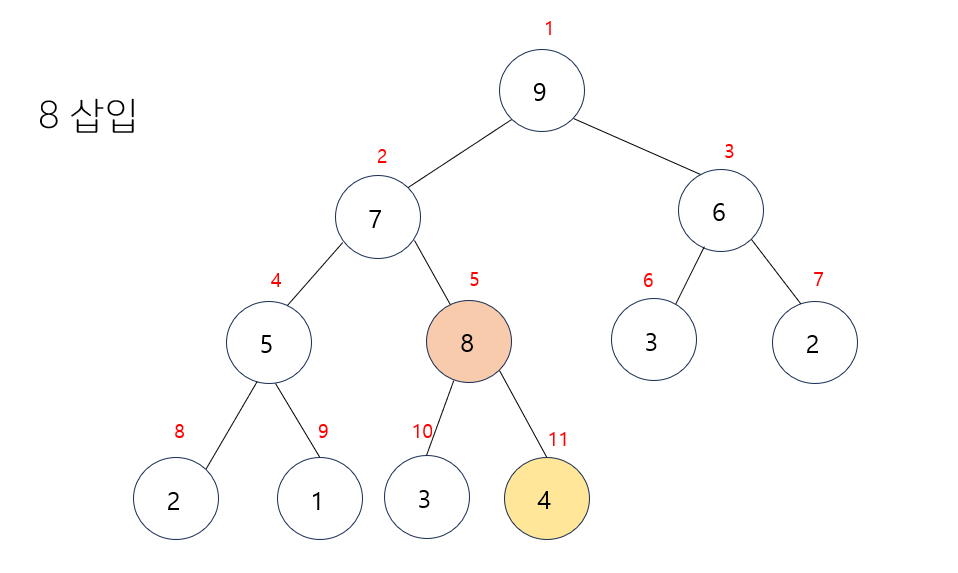
• 부모노드보다 현재노드인 8이 더 크기에 자리를 변경한다.

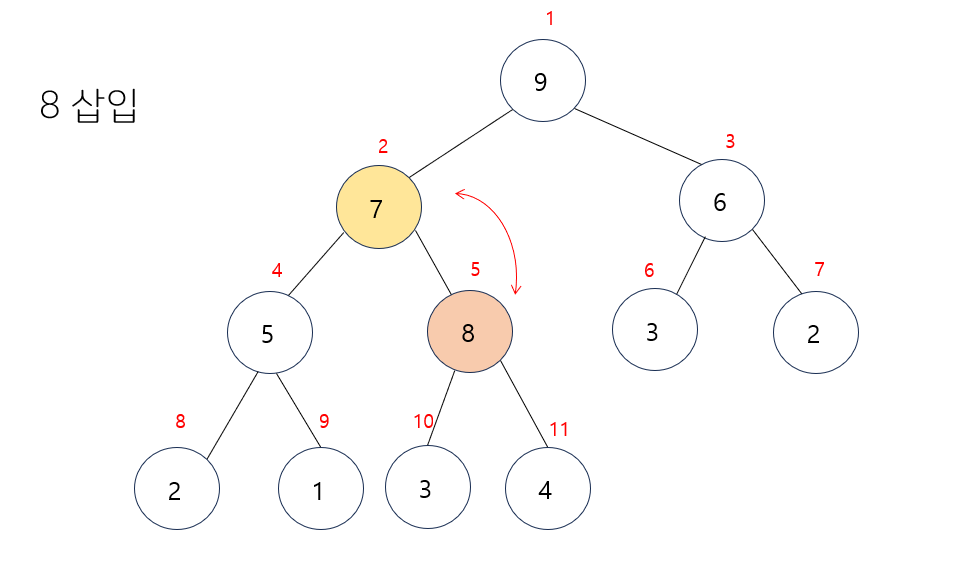
• 루트노드 까지 또 다시 부모노드와 비교를 한다.

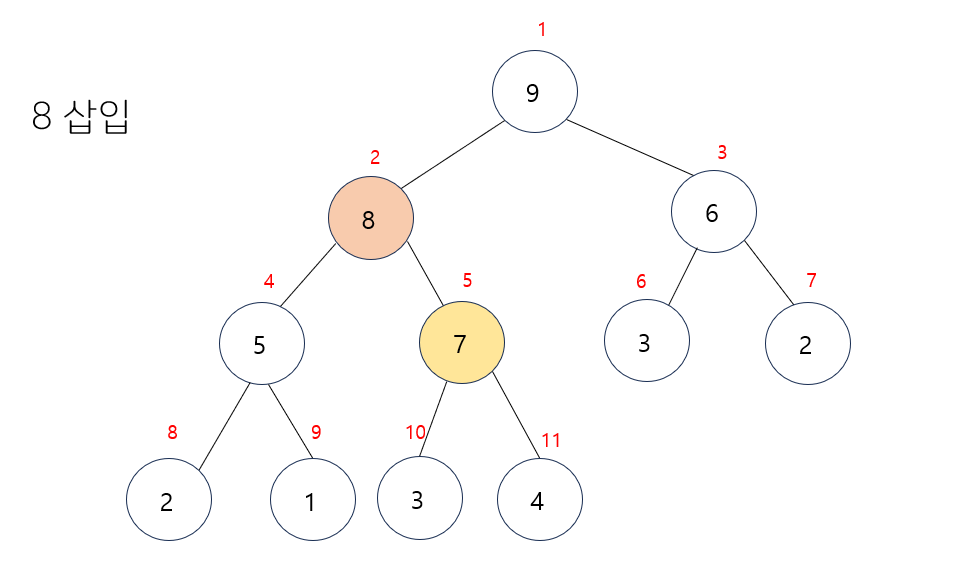
• 마찬가지로 부모노드보다 현재노드값이 더 크기에 자리를 변경해준다.

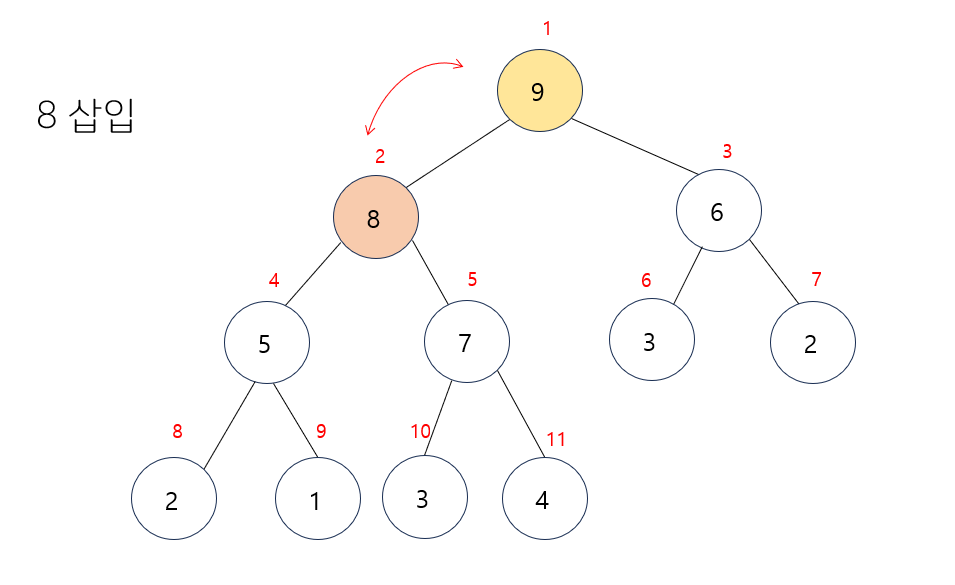
• 마지막 루트노드인 9와 삽입하는 노드 8을 비교한다.

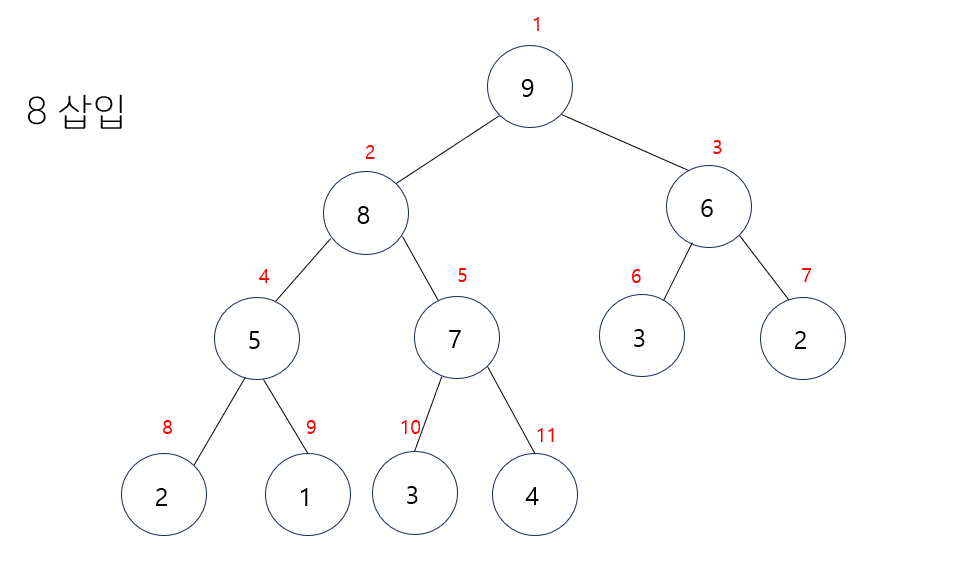
• 부모노드가 더 크기에 자리를 변경하지 않으므로 삽입연산을 마친다.
  
  

히프 삽입연산 코드

typedef struct{
    int key; 
}element; // 히프의 각 요소

typedef struct{
    element heap[100]; // 히프를 구현할 1차원 배열
    int heap_size; // 현재 히프안에 저장된 요소의 갯수
}HeapType;

void insert_max_heap(HeapType* h, element item) // 삽입 연산 함수
{
    int i;
    i = ++(h->heap_size); // i를 증가시켜 히프의 마지막 노드에 삽입

    while((i != 1) && (item.key > h->heap[i / 2].key)){ // i가 루트노드가 아니고, 삽입할 원소가 부모노드이 키 값보다 큰 경우
        h->heap[i] = h->heap[i / 2]; // 현재 위치 i를 부모노드의 값으로 변경
        i /= 2; // 부모노드 인덱스로 이동
    }
    h->heap[i] = item; // 최종 위치 i에 원소 삽입
}

히프 삭제연산

• 제일 최대값(최소값)인 루트노드를 제거
• 히프트리 재구성

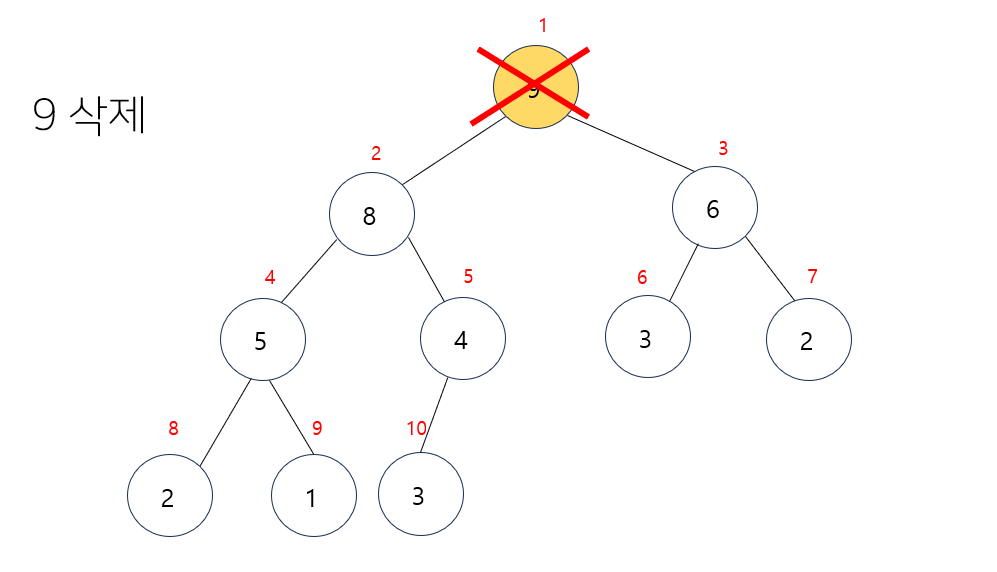
• 루트노드(최대값)인 9 삭제

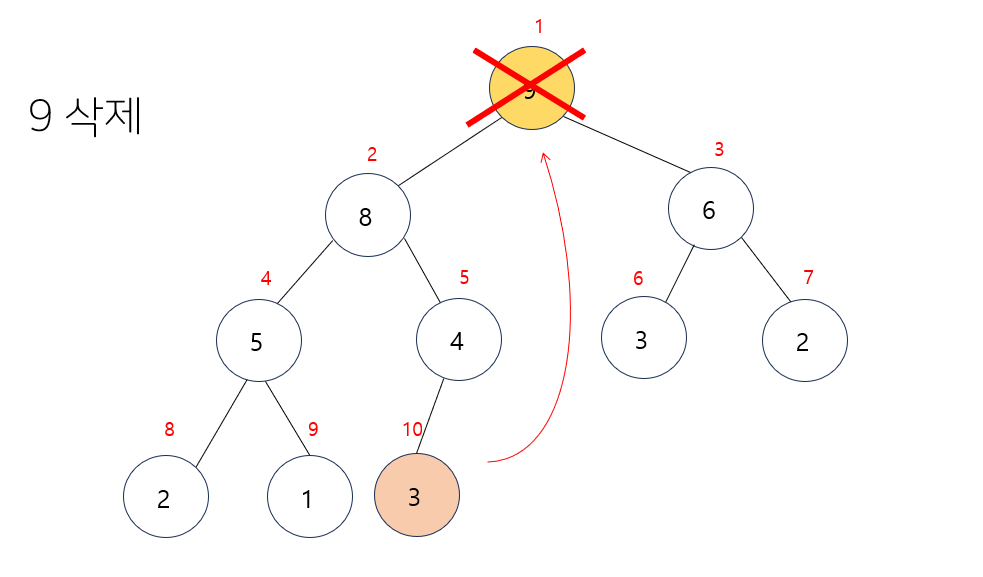
• 가장 끝에 달려있는 노드를 루트노드로 이동

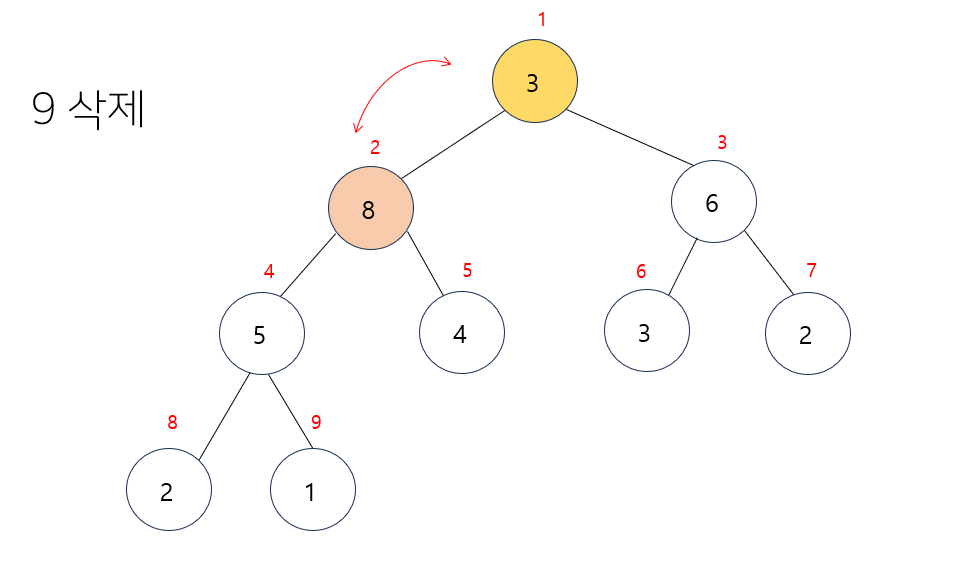
• 최대히프 조건을 만족시키기 위해 자식 노드를 비교하여 더 큰 값으로 변경

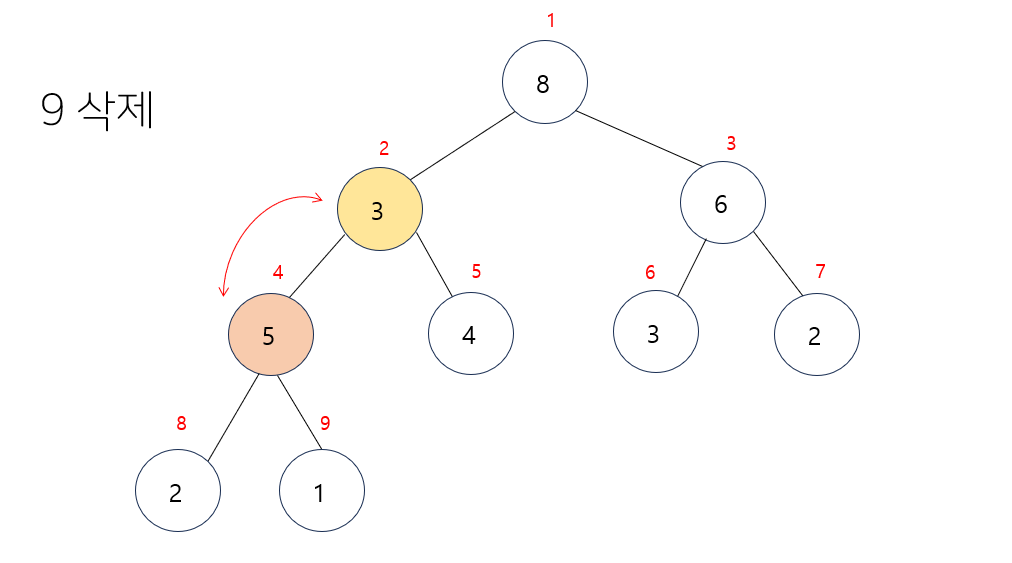
• 다시 한번 자식노드와 비교하여 둘 중 더 큰 값으로 변경

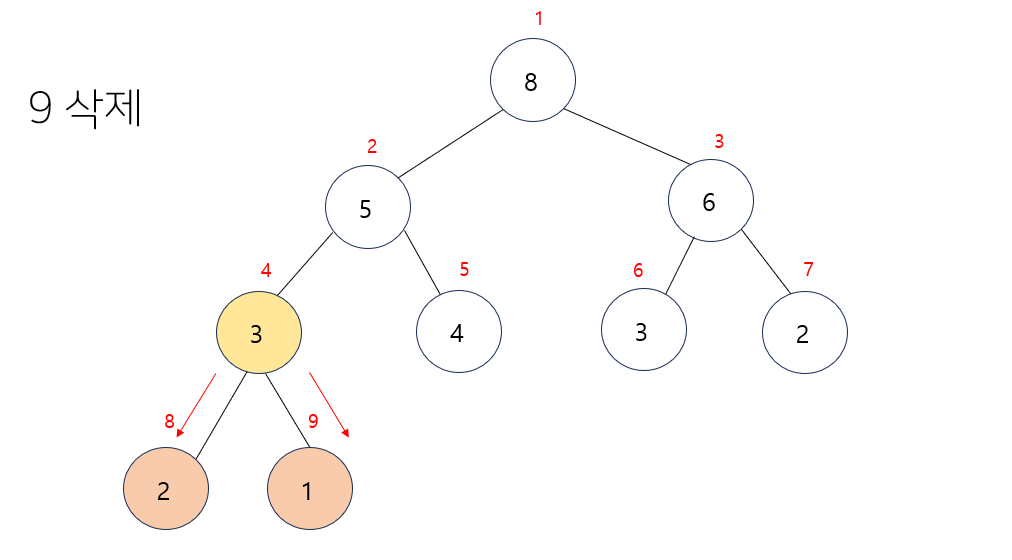
• 또 자식노드와 비교를 하는데 자식노드보다 크기에 변경하지 않음

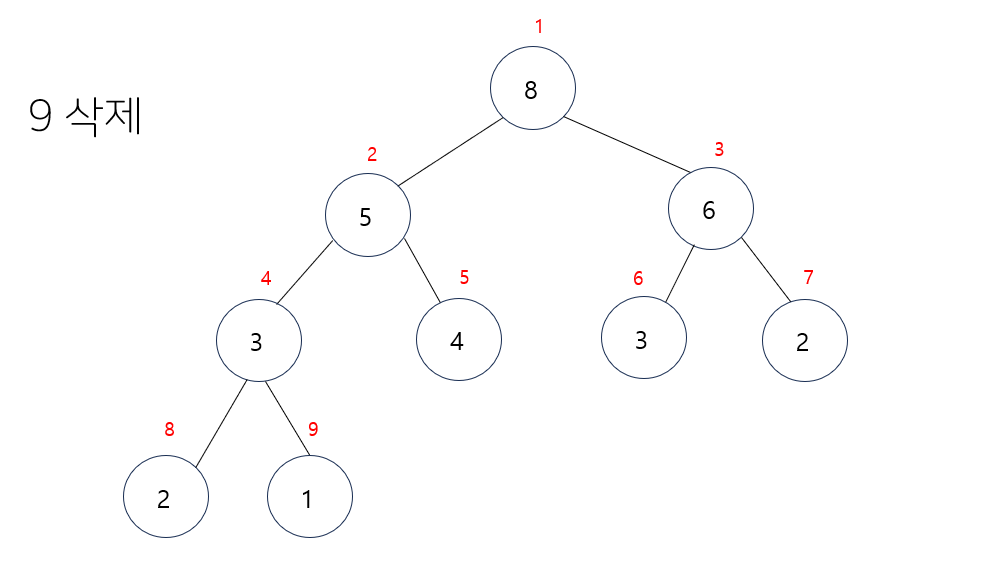
• 삭제연산을 마친 히프의 모습
  
  

히프 삭제연산 코드

element delete_max_heap(HeapType* h) // 삭제연산 함수
{
    int parent, child; // 부모노드와 자식노드의 인덱스
    element item, temp;

    item = h->heap[1]; // 삭제할 루트노드의 값 저장
    temp = h->heap[(h->heap_size)--]; // 히프의 마지막값 저장 후 사이즈 감소
    parent = 1;
    child = 2;

    while(child <= h->heap_size){ // 자식노드가 존재할 때까지 반복
        if ((child < h->heap_size) && (h->heap[child].key) < h->heap[child + 1].key) // 현재 자식노드의 인덱스가 히프의 크기를 벗어나지 않고 오른쪽 자식노드의 키값이 더 큰 경우
            child++; // child를 증가시켜 오른쪽 자식노드의 인덱스로 이동

        if(temp.key >= h->heap[child].key) // 마지막 노드의 키 값이 현재 자식노드의 키 값보다 큰 경우 종료
            break;

        h->heap[parent] = h->heap[child]; // 자식노드를 부모노드의 위치로 이동
        parent = child;  // parent와 child 인덱스를 이동시켜 다음 자식과 비교
        child *= 2;
    }
    h->heap[parent] = temp; // 최종적으로 마지막 노드가 저장될 위치
    return item; // 삭제할 원소 반환
}