트리(Tree)란?
- 트리는 계층적인 자료를 표현하는데 적합한 자료구조이다.
- 한 개 이상의 노드로 이루어진 유한 집합이다.
- 트리에는 사이클(cycle)이 존재할 수 없다.
- 사이클이 없는 하나의 연결 그래프, 방향성이 있는 비순환 그래프의 한 종류
- 그래프의 한 종류로 '최소 연결 트리'라고도 불린다.
트리의 구조
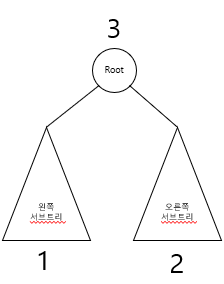
- 하나의 노드는 루트(root)노드라 불리고 나머지 노드들은 서브 트리라고 불린다.
- 계층적인 구조에서 가장 높은 곳에 있는 노드가 바로 루트노드이다.
- 서브 트리 안에서도 가장 높은 노드는 루트이고 나머지 서브트리로 구성되어 있다.
- 트리에서 루트와 서브 트리는 선으로 연결된다. 이 선을 간선이라고 한다.
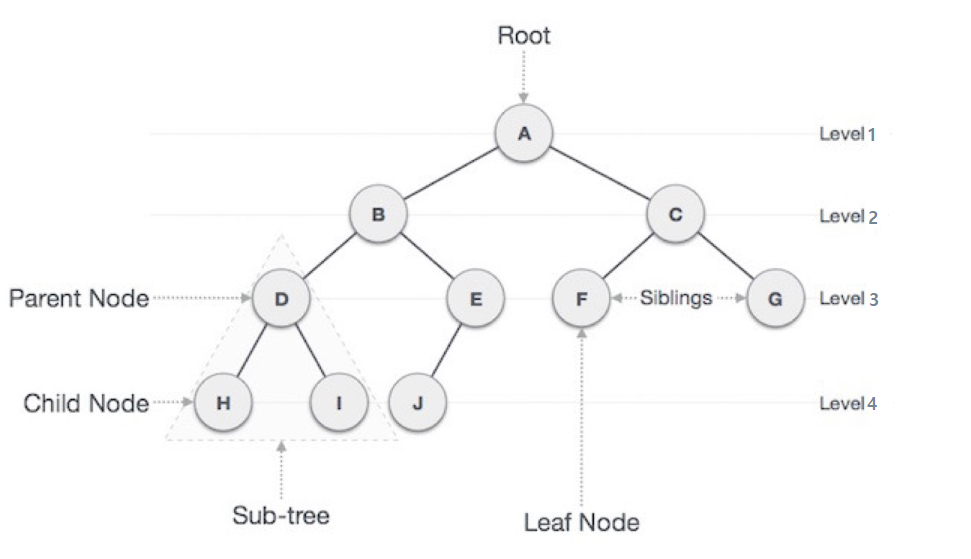
-
루트 노드(root node) : 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
-
단말 노드(leaf node) : 자식이 없는 노드
-
비단말 노드(nonterminal node) : 자식이 있는 노드, 내부 노드라고도 불림
-
간선(edge) : 노드를 연결하는 선
-
조상 노드 : 루트 노드에서 임의의 노드까지의 경로를 이루고 있는 노드들
-
후손 노드 : 임의의 노드 하위에 연결된 모든 노드들
-
형제 노드(siblng node) : 같은 부모를 가지는 노드
-
노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수
-
노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
-
노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합(루트 노드부터 레벨 1)
-
노드의 차수(degree) : 어떤 노드가 가지고 있는 자식 노드의 개수(단말노드는 차수 0)
이진트리란?
- 모든 노드가 2개의 서브 트리를 가지고 있는 트리
- 서브 트리는 공집합일 수 있다.
- 이진트리의 노드에는 최대 2개까지의 자식 노드가 존재할 수 있고 모든 노드의 차수가 2 이하가 된다.
이진트리의 성질
- n개의 노드를 가진 이진트리는 정확하게 n-1개의 간선을 가진다.
- 높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지며 최대 개의 노드를 가진다.
이진트리의 분류
1. 포화이진트리(Perfect Binary Tree)
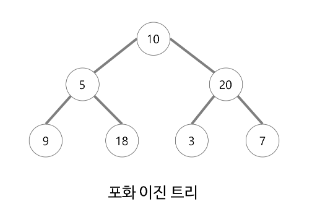
- 트리의 각 레벨에 노드가 꽉 차있는 이진트리
- 높이 k인 포화 이진트리는 정확하게 개의 노드를 가진다.
- 각 노드에 레벨 단위로 왼쪽에서 오른쪽으로 번호를 붙인다.
- 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
2. 완전이진트리(Complete Binary Tree)
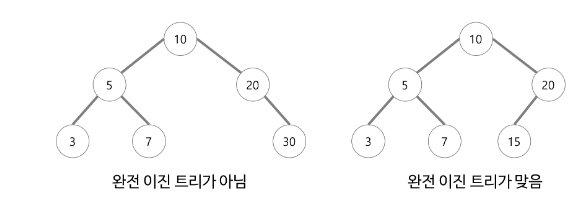
- 높이가 k일 때 레벨 1부터 k-1레벨 까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리이다.
- 마지막 레벨에서는 노드가 꽉차있지 않아도 되지만 중간에 빈 곳이 있어서는 안된다.
- 포화이진트리는 항상 완전이진트리이지만 완전이진트리는 항상 포화이진트리는 아니다.
3. 전 이진트리(Full Binary Tree)
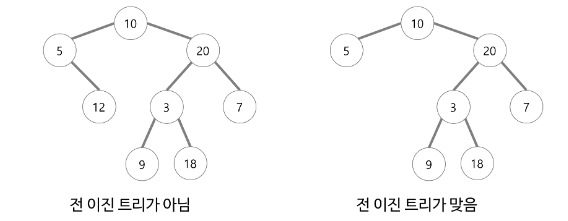
- 모든 노드가 0개 또는 2개의 자식을 갖는 트리
이진트리 순회 방법
- 이진트리를 순회하는 표전적인 방법에는 전위, 중위, 후위의 3가지 방법이 있다.
1. 전위 순회(preorder)
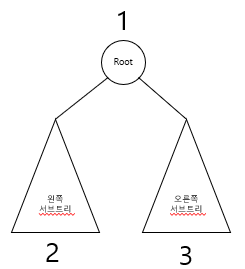
- 먼저 루트 노드를 방문한다.
- 왼쪽 서브트리를 방문한다.
- 오른쪽 서브트리를 방문한다.
전위 순회를 하는 코드는 다음과 같다.
void preorder(TreeNode* root) { // 전위 순회 출력
if (root != NULL) {
printf("[%d] ", root->data);
preorder(root->left);
preorder(root->right);
}
}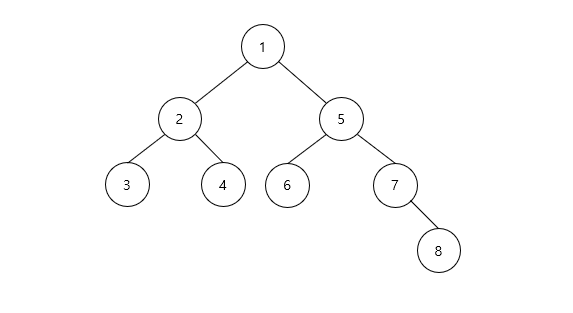
- 위 트리는 전위 순회의 방문 순서를 보여준다.
2. 중위 순회(inorder)
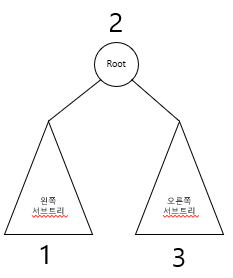
- 먼저 왼쪽 서브트리를 방문한다.
- 루트노드를 방문한다.
- 오른쪽 서브트리를 방문한다.
중위 순회를 하는 코드는 다음과 같다.
void inorder(TreeNode* root) { // 중위 순회 출력
if (root != NULL) {
inorder(root->left);
printf("[%d] ", root->data);
inorder(root->right);
}
}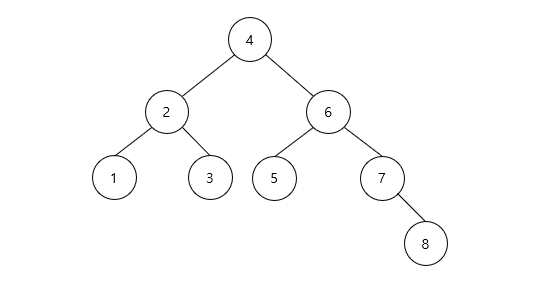
- 위 트리는 중위 순회의 방문 순서를 보여준다.
3. 후위 순회(postorder)
- 먼저 왼쪽 서브트리의 모든 노드를 방문한다.
- 오른쪽 서브 트리의 모든 노드를 방문한다.
- 루트노드를 방문한다.
후위 순회를 하는 코드는 다음과 같다.
void postorder(TreeNode* root) { // 후위 순회 출력
if (root != NULL) {
postorder(root->left);
postorder(root->right);
printf("[%d] ", root->data);
}
}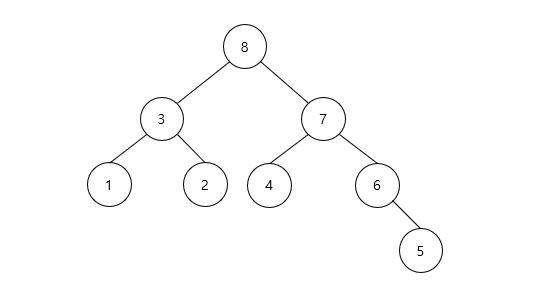
- 위 트리는 후위 순회의 방문 순서를 보여준다.
레벨 순회란?
- 레벨 순회(level order)는 각 노드를 레벨 순으로 검사하는 순회 방법이다.
- 레벨 순회는 큐를 사용하는 순회법이다.
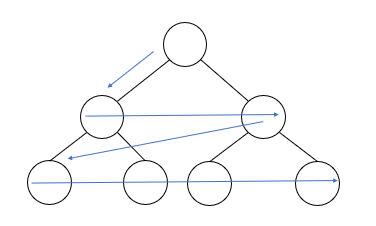
- 루트 노드의 레벨이 1이고 아래로 내려갈수록 레벨은 증가한다.
- 동일한 레벨의 경우에는 좌에서 우로 방문한다.
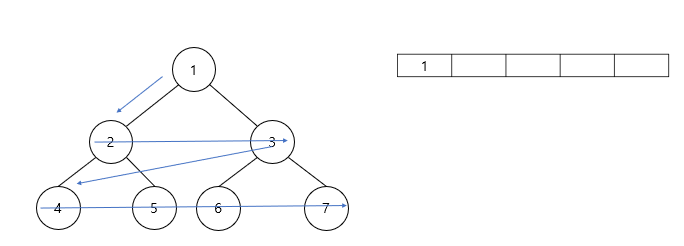
- 1번 루트노드를 Queue에 저장한다.
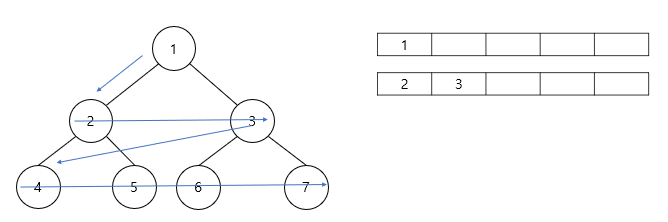
- Queue에 있는 1번 노드를 방문하여 연결된 자식노드 2, 3번 노드를 Queue에 저장한다.
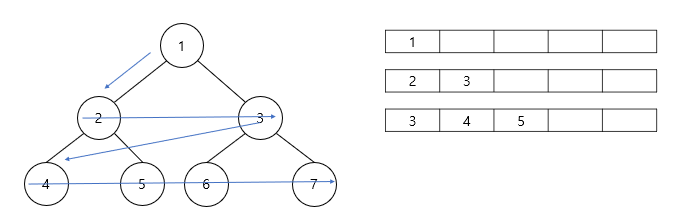
- Queue의 맨 앞에있는 2번 노드를 방문하여 마찬가지로 연결된 자식노드 4, 5번 노드를 Queue에 저장한다.
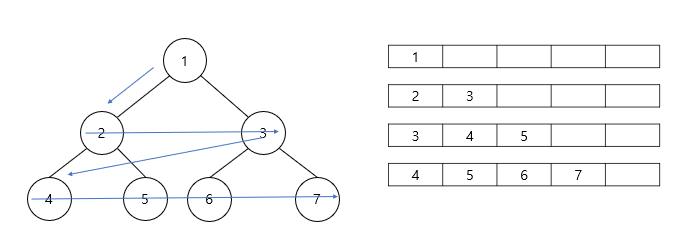
- Queue의 맨 앞에있는 3번 노드를 방문하여 연결된 자식노드 6, 7번 노드를 Queue에 저장한다.
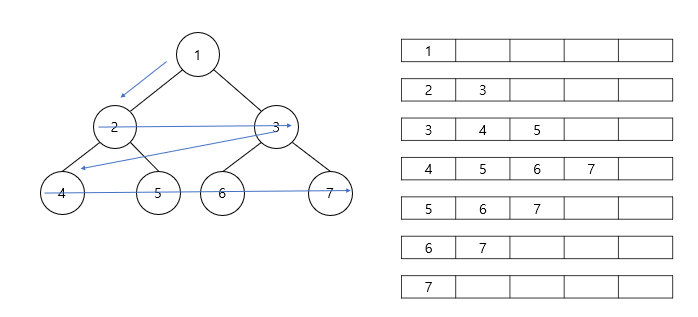
- Queue에 남아있는 노드가 없을때 까지 반복하여 나머지 4~7번 노드까지 방문하여 마친다.