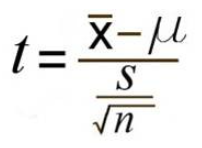이전에 기술통계기법과 추리통계기법을 알아보았는데, 추리통계(가설세우고 추측,예측)에 대해 더 자세히 알아보자.
링크 : 기술통계vs추리통계
1. 샘플링하는 방법
방대한 데이터를 추론,예측하고 싶을 땐, 모집단(전체데이터)로부터 표본(샘플)을 뽑아 가설을 세울 수 있다. 이때 대부분 모집단에 대한 정보는 모르는 상태로 표본만 뽑아 알고 싶은 정보에 대해 가설을 세우는 것이다. 샘플링 하는 방법은 4가지로 나눌 수 있다.
- 모집단에서 무작위 선출 (simple random sampling)
: 말그대로 무작위로 샘플을 뽑는 것이다.
넘파이 사용해 랜덤 추출하기 :
np.random.randint(숫자 몇 부터 , 몇 까지 ,몇개 )
np.random.seed(숫자)
np.random.binomial(n = , p = , size = 샘플사이즈)- 모집단에서 규칙을 가지고 추출 (Systematic sampling)
: 예를들어 5의 배수만 추출 - 계층화 랜덤 추출 (Stratified random sampling)
: 그룹을 나누고 그룹에서 특정 개수 추출 - 군집화 추출 (Cluster sampling)
: 그룹을 나누고 특정그룹에서만 무작위 선택
TIP :표본의 수(샘플의 사이즈)가 많을 수록, 추측은 정확해지고 높은 확률로 모집단에 대한 예측을 할 수 있다. (표본평균의 표준오차 공식을 통해 알수있음.)
2. 가설검정 (Hypothesis Test)
위키피디아 : Statistical Hypothesis testing
A statistical hypothesis is a hypothesis that is testable on the basis of observed data .....
통계적 가설은 관측데이터를 바탕으로 검정할수있는 가설이다.
통계학의 목적은 표본으로부터 얻은 정보로 모집단에대해 추론하는 것이다.
-
가설검정이란 :
주어진 상황에 대해 하고자 하는 주장이 맞는지 아닌지를 판정하는 과정.
모집단의 실제 값에 대한 sample 의 통계치를 사용해서 통계적으로 유의한지 아닌지 여부를 판정 -
가설검정하는 방법 :
- 가설 세우기(귀무가설과 대립가설로 나뉜다)
- 유의수준 정하기(기본 신뢰도 95% 많이 사용)
- 단측검정(1 sided test)할지 양측검정(2 sided test)할지 정하기.
- 샘플링해서 검정통계량(확률변수) 계산 후 p값 계산
- 결론(계산한 P값<=유의수준이면 귀무가설 기각, 반대면 채택.)
가설검정방법에는 여러가지가 있는데 Student T-Test , Chi-Square Test, Anova 등이 있다. 가설 상황에 따라서 적재적소에 방법을 적용해야한다. 각 테스트가 무엇을 알아보는 테스트인지 안다면 내가 설정한 가설에 어떤 테스트를 사용해야할지 쉽게 구분 할 수 있을 것이다.
2-1. Student T-TEST
Student t-test T-test Small-sample Hypthesis Testing
one-sample test VS two-sample test
one-tailed test VS two-tailed test (tailed = sided = direction)
T-test 는 정규모집단에서 추출한 소표본(small size sample)의 평균을 특정값(모집단과 관련된)과 비교하는 검정방법이다. 1개의 sample 값을 비교하는 one-sample T-test와 2개의 sample 값을 비교하는 two-sample T-test가 있다. 그리고 각 T-test에는 One-tailed test(평균이 큰지 작은지 검정)와 Two-tailed test(평균이 같은지 같지않은지 검정)가 있다.
💡 T-test의 4가지 조건
- 자료는 모두 동일 간격을 가진 연속형 수치여야 한다(identical interval and continuity)
샘플이 순위척도자료 또는 10개이하의 연속형자료 : Mann-Whitney test 사용
샘플이 10개이상 30개이하의 연속형자료일 때 정규성이면 t-test 정규성이 아니면 Mann-Whitney test
샘플이 30개 이상의 연속형자료이면 t-test- 두 집단은 서로 독립적 이어야 한다. (independence)
만족하지 못하는 경우에는 대응표본T검정 or Wilcoxon signed rank test 적용- 자료의 수치는 정규성 가져야한다. (normality)
만족하지 않는 경우에는 자료들의 순위의 합을 이용하는 비모수적인 방법인 Mann-Whitney test를 사용정규화 확인 from scipy.stats import normaltest normaltest(sampledata)
- 두 집단 각각에서 추정된 분산은 동일해야한다. (equal variance)
만족하지 못하는 경우엔 Welch's T test를 사용해 두 집단차이를 분석하거나 자유도를 수정한 t-test 를 사용.
<검정통계량 구하는 공식과 정규분포>
검정통계량 = 표본 측정값의 함수(이러한 과정을 정규화라고 하며 정규화를 하면 주어진 데이터가 평균은0, 표준편차가 1인 데이터로 scaling이 된다)
t=표본평균-특정값/표준오차
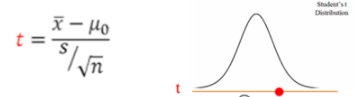
📢귀무가설 H0: =o 가 참일 때 t검정통계량은 n-1의 자유도를 갖는 t분포를 따른다.
📢t분포가 대칭적으로 가운데가 불룩한 현상이므로, 귀무가설에 대한 소표본검정의 기각역(Rejection Region)은 t분포의 꼬리쪽에 위치하며 z-test와 비슷하다.
1. One-sample T-test
: 1개의 sample 값들의 평균이 특정값과 동일한지(2tail) 혹은 크거나 작은지(1tail) 비교
- 모평균(), 모분산(σ2) 을 모르는 정규분포
- 특정값(o)
- 모집단으로부터 표본(샘플) [ X1,X2,,,,Xn ] n개 추출
- 표본평균(X`), 표본표준편차(S)
- 분모 : 표본의 표준오차=표본평균의 표준편차(표본의 표준편차/샘플개수n의 제곱근)
- 가정 : X1,X2,,,Xn은 E(X i)=인 정규분포로부터 얻어진 랜덤표본이라고 하자.
- 귀무가설 H0
H0 : = o - 대립가설 Ha
Ha : > o (one tailed alternative 단측검정, upper tail 오른쪽꼬리)
Ha : < o (one tailed alternative 단측검정, lower tail 왼쪽꼬리)
Ha : != o (two tailed alternative 양측검정) - 신뢰도 설정하기 : 모수가 신뢰구간 안에 포함될 확률(보통 95%, 99%등을 사용)
기각역 (Rejection Region)
유의수준, P-Value와 관련이 있다반대는 채택역(acceptance region)
a=귀무가설이 맞지만 기각될 오류의 확률100(1-a)% : 신뢰구간
RR : t > ta (upper tail RR)
RR : t < -ta (lower tail RR)
RR : |t| > t*a/2 (two tailed RR)
- a는 검정의 유의수준 또는 검정수준이라 불린다. 관습적으로 a는 0.05 또는 0.01이 사용된다.
- T를 검정 통계량이라고 할 때, 'p-value'혹은 '획득된 유의수준'은 관측된 데이터가 귀무가설을 기각시킬 수 있는 가장 작은 유의수준 a이다. (=주어진 가설에 대해 얼마나 근거가 있는지에 대한 값. 0과 1사이의 값으로 scale한 지표이다.)`
- P값이 작을 수록 귀무가설을 기각할수 있는 증거는 강력해진다. p값을 바탕으로 가설에 대한 결론을 내릴 수 있다.
- t가 기각역에 빠지면 귀무가설 H0를 기각한다.
사이파이 코드
from scipy import stats
stats.ttest_1samp(샘플의데이터, 비교하려는 평균값, axis=0, nan_policy='propagate', alternative={'two-sided'’, ‘less’, ‘greater’})
2. Two-sample T-test
: 2개의 sample 값들의 평균이 서로 동일한지 혹은 크거나 작은지 비교
두개의 정규 모집단이 동일한 분산(등분산)을 가질 때 소표본으로부터 모집단의 평균을 비교하는 것.

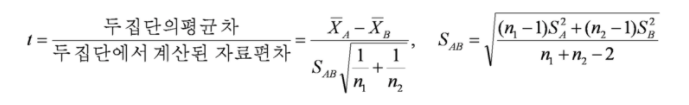
- 귀무가설 H0
1 - 2 = D0(고정된값) - 대립가설 H*a
1 - 2 > D0 (One tailed alternative 단측검정, upper tail 오른쪽꼬리)
1 - 2 < D0 (One tailed alternative 단측검정, lower tail 왼쪽꼬리)
1 - 2 != D0 (Two tailed alternative 양측검정) - 검정 통계량

- 기각역
t > ta (upper tail RR)
t < -ta (lower tail RR)
|t| > t*a/2 (Two tailed RR) - P(T > t*a)
- 자유도 : 표본1의개수 + 표본2의개수 - 2
자유도가 클수록 표준정규분포(standard normal distribution)에 가까워지는 특성이 있다.사이파이 코드
from scipy import stats
stats.ttest_ind(샘플의데이터1,샘플의데이터2, axis=0, equal_var=True, nan_policy='propagate',Alternative={‘two-sided’, ‘less’, ‘greater’})
3-2 Anova test (F-test)
: 그룹이 3개이상인 경우 그룹이 같은지 다른지 알고싶을 때 사용
참고 :Youtube (Sapientia a Dei)
1. One-way ANOVA (일원분산분석)
: 종속변인은 1개이며, 독립변인의 집단도 1개인 경우. 한가지 변수의 변화가 결과 변수에 미치는 영향을 보기 위해 사용된다.(=F값구하기)
- 종속변수 : 연속형(Continuous)변수만 가능
- 독립변수 : 이산형/범주형(Discrete/Categoricl) 변수만 가능
예시) 아이들의 폭력성을 실험하기 위해 세 그룹에 폭력영화, 드라마, 공익광고를 보여준 후 한 곳에 모아 폭력행동에 대해 점수를 매겨보았다. 이때 아이들의 폭력행동 점수는 종속변수, 영상의 종류는 독립변수이다.(독립변수는 Level이 3개일뿐 총 1개이다 )
- 귀무가설 : 1 = 2 =...= k (k=그룹의 개수)
- 대립가설 : i != j (적어도 한 그룹의 평균은 다르다.)
- 자유도 : n-1 (첫번째 분산의 자유도 + 두번째 분산의 자유도)
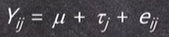
- $\mu% : 평균
- r(타우) : 독립변수 / j: 그룹
- Y : 종속변수 / i: 그 그룹 내의 ID
- e : 오차(error)
F-value (F값) 이란?
: 두개의 분산의 비율(분산분석이라 부르는 이유)
첫번째분산/두번째분산
- 첫번째 분산 : GM(전체평균)으로부터 각 그룹의 평균 사이 분산 (Between Variance)
자유도1 : df1= k-1 (k는 그룹의 개수)
Between Variance 가 크다 = 전체 평균으로부터 각 그룹의 평균이 멀리 떨어져 있다. = 적어도 어떤 그룹 한개는 다른 그룹과 평균이 다를 수 있다.
하지만 얼마나 커야 통계적으로 큰 걸까? 즉, 이 Between Variance가 우연히 클 가능성은 확률적으로 얼마나 될까? -> Between Variance와 비교할 다른 Variance가 필요함(=두번째분산) - 두번째 분산 : 전체그룹 내의 분산 (Within Variance)
자유도2 : df1= n-k (n은 샘플의크기, k는 그룹의 개수)
T-test에서의 분모의 표준편차와 같은 의미
결론 : Betwwen Variance 가 Within Variance보다 충분히 커야 우리는 Betwwen Variance가 통계적으로 크다고 말할 수 있고, 이것은 적어도 어느 한 그룹의 평균값이 전체 평균과는 다르다고 할 수 있다.
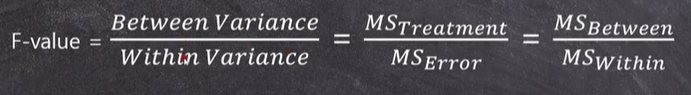
- 결론적으로, t-값과 마찬가지로 우리의 관심인 분자부분의 분산을 비교대상인 분모부분의 분산과 비교하여 비율로써 나타낸 값이 F갑시다.
- 분모의 within variance는 random한 변동값으로, between variance가 이보다는 훨씬 커야 한다는 것을 의미함.
사후검정(Post Hoc Tests)의 필요
: 만약 세 그룹이 유의한 차이가 있다(대립가설채택)이 나온다면, 어떤 그룹이 어떻게 유의한지 알 수가 없음. 그래서 ANOVA에서는 유의하다는 결과가 나오면 자동으로 사후검정을 해야함.
- 사후검정이란? : 일종의 여러 다발의 t-test 그러나 Type-1-error를 발생시키지 않음. 각 그룹의 평균이 다른 그룹의 평균과 같은지 다른지 개별 비교 가능.
- 사후검정의 종류 : Fisher's LSD/Bonferroni/Sheffe/Tukey/Duncan (아무거나쓰면됨)
- 그래프사용.
파이썬 코드
1. 사이파이 코드를 사용한 일원분석
import scipy.stats as stats
F_statistic, pVal = stats.f_oneway(group1, group2, group3)
- Statsmodel을 사용한 일원분(훨씬 간편하고 깔끔한결과)
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
import warnings
warnings.filterwarnings('ignore')
df = pd.DataFrame(data, columns=['value', 'treatment'])
#the "C" indicates categorical data
model = ols('value ~ C(treatment)', df).fit()
print(anova_lm(model))
- 사후분석하기(Tukey test)
from statsmodels.stats.multicomp import pairwise_tukeyhsd
posthoc = pairwise_tukeyhsd(df2['value'], df2['treatment'], alpha=0.05)
print(posthoc)
2. Two-way ANOVA (이원분산분석)
: 독립변인의 수가 두 개 이상일 때 집단 간 차이가 유의한지를 검증하는 데 사용.
첫번째 독립변수에서 종속변수가 변화할 것이라고 예측하고, 동시에, 두번째 독립변수에서 종속변수가 변화할 것이라고 예측함. 여기서 독립변수는 Main effect(주효과)가 있다고 함. 이원분산분석엔 Main effect가 2개.
통계적 가설 3개 필요
-
첫번째 mail effect에 대한 통계적 가설
귀무가설1 : 11 = 12 =...= 1k (k=그룹의 개수)
대립가설1 : 1i != 1j (적어도 한 그룹의 평균은 다르다.)
자유도 : k1-1(kn=n번째 독립변수의 그룹 개수) -
두번째 mail effect에 대한 통계적 가설
귀무가설2 : 22 = 22 =...= 2k (k=그룹의 개수)
대립가설2 : 2i != 2j (적어도 한 그룹의 평균은 다르다.)
자유도 : k2-1(kn=n번째 독립변수의 그룹 개수) -
Interaction에 대한 통계적 가설
귀무가설3 : 상호작용효과가 존재하지않는다.
대립가설3 : 상호작용효과가 존재한다.
자유도 : 첫번째자유도 * 두번째자유도
이원분산분석의 특징
-
상호작용효과(Interaction effect) : 한 변수의 변화가 결과에 미치는 영향이 다른 변수의 수준에 따라 달라지는지를 확인하기 위해 사용된다. (한 독립변수의 종속변수에 대한 영향관계가 다른 독립변수의 Level(=group)에 따라 변할 경우, 상호작용이 있다고함)
-
(직)선형관계(Linear relationship) : 독립변수와 종속변수의 관계가 (직)선형관계라고 이미 전제된 것. 즉, t-test이든 ANOVA이든 이미 사전에 (직)선형관계는 전제되었던 것임.
일원분산분석에서과 다른점
- 독립변수가 2개
- 따라서, F값도 2개
- 추가적으로 interaction도 유의한지 아닌지 알아야함
- 따라서, interaction에 대한 F값도 한개 더 필요함.
- 총 3개의 F값이 필요.

- Within Variance(분모)는 모두 동일함
자유도(df within) : (r-1) k1 k2 (r=각 셀의 실험 회수, kn=n번째 독립변수의 그룹 개수)
사후검정
- 첫번째 main effect가 유의할 경우 -> 사후검정필요
- 두번째 main effect가 유의할 경우 -> 사후검정필요
- Interaction이 유의할 경우 -> 사후검정필요(?),가능은 하지만 매우 복잡하니 그래프를 그려보는 것이 좋음.
파이썬 코드
1. statsmoel로 Anova test하기
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
ex)아기 3명의 머리둘레 차이
formula = 'head_size ~ C(fetus) + C(observer) + C(fetus):C(observer)'
lm = ols(formula, df).fit()
print(anova_lm(lm))
2. 사후분석하기(Tukey test)
from statsmodels.stats.multicomp import pairwise_tukeyhsd
posthoc = pairwise_tukeyhsd(df2['value'], df2['treatment'], alpha=0.05)
print(posthoc)
3-2 Chi-square test (카이제곱검정)
변수가 명목척도 일 때, 자료(데이터)값은 개수(count)이어야 함
: 자료가 빈도와 같이 범주형 자료일 경우 기존 T-test와 같은 방법으로 분석이 불가능하다. 독립변수와 종속변수의 연관성의 유의성을 검정하는 것을 교차분석이라고 하며, 대표적으로 카이제곱 검정이 있다. 즉, 카이제곱검정은 두 변수가 연관성이 없는지(독립사건인지), 연관성이 있는지(종속변수인지) 판별하는 것이다.
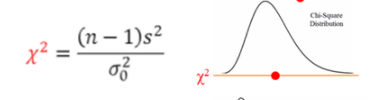
1. One-way Chi-square-test (일원 카이제곱 검정)
변수1개
- 적합도 검정(goodness of fit) : 관측값이 기대분포를 따르고 있는지에 대한 검정. 검정을 위해서 자료를 categorical data로 변환해주어야 한다. 하나의 요인을 대상으로 함.
- 단, 그룹이 단 2개인 경우 : Binomial test , 그룹이 여러개인 경우 : Chi square-test
귀무가설: 관측값과 기대분포의 기대값이 동일하다.
대립가설: 관측값과 기대분포의 기대값이 다르다.
자유도(k): n-1
검정통계량: Obs , Exp=sum(obs)/count
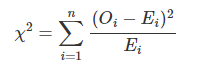
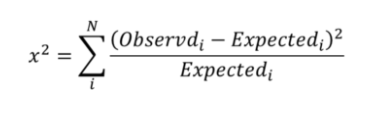
사이파이로 일원카이제곱검정
from scipy.stats import chisquare
chisquare(data)
통계치로 p-VALUE 구하기
print(1-stats.chi2.cdf,df=(n-1))
2. Two-way Chi-square-test (이원 카이제곱검정)
변수2개 two-way : 주로 2x2분할표 사용
-
독립성 검정(test of independence) : 두개의 요인들이 서로 연관이 있는지를 검정. (즉 X와 Y는 서로 독립인지 종속인지 판단) 두개의 요인을 대상으로 함
귀무가설 : 종속변수와 독립변수가 독립 사건이다.(두 변수는 연관성이없다)
대립가설 : 종속변수와 독립변수가 종속 사건이다.(두 변수는 연관성이있다)
( = 기대빈도와 차이가 크다)
자유도(K) : (X의 범주 수-1)*(Y의 범주 수-1)
검정통계량:
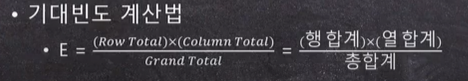
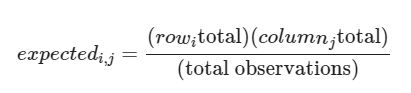
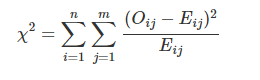
-
그 외:
동질성 검정(test of homogeneity) : 관측값이 정해진 범주 내에서 서로 비슷한지를 검정. 두개의 요인을 대상으로 함.
Likelihood-ratio test
Log-rank test
카이제곱검정의 한계 or 전제조건
- 랜덤샘플링
- 독립성 : 각 범주가 서로 배타적이어야함, 한 대상이 하나 이상의 범주에 들어갈 수 없음
- 기대빈도가 5미만인 셀이 전체의 20%를 초과하는 경우는 가설검정 결과가 정확하지 않을 수 있다.
기대빈도를 5이상으로 맞추기 위해 경우에 따라 범주를 합쳐야 함. 합칠 수 없다면, 피셔의 정확검정(Fisher's exact test)를 하거나 likelihood ratio test(G-test)를 해야함. - 많은 표본을 확보하는 것이 결과의 신뢰도를 크게 높일 수 있다.
만약 자유도가 1이라면(범주가 2개이거나 이원카이제곱검정에서 2X2인경우) 비연속성의 조건부 확률을 연속성의 카이제곱분포에 적용함으로써 문제 발생.
일원카이제곱검정의 경우 무조건 연속성 보정을 하는 Yate's correction 또는 카이제곱 continuity correction을 사용해야함. 다만, 이원 카이제곱 검정의 2x2인 경우 카이제곱테스트의 결과와 Yate's correction의 결과가 다를 때에는 Fisher's exact test 사용
사이파이로 이원카이제곱검정
from scipy.stats import chi2_contingency
chi2, pval, dof, expected = chi2_contingency(data, correction = False)통계치로
p-VALUE 구하기
print(1- stats.chi2.cdf(통계치, df = ((열변수 개수-1)*(행변수 개수-1)) ))
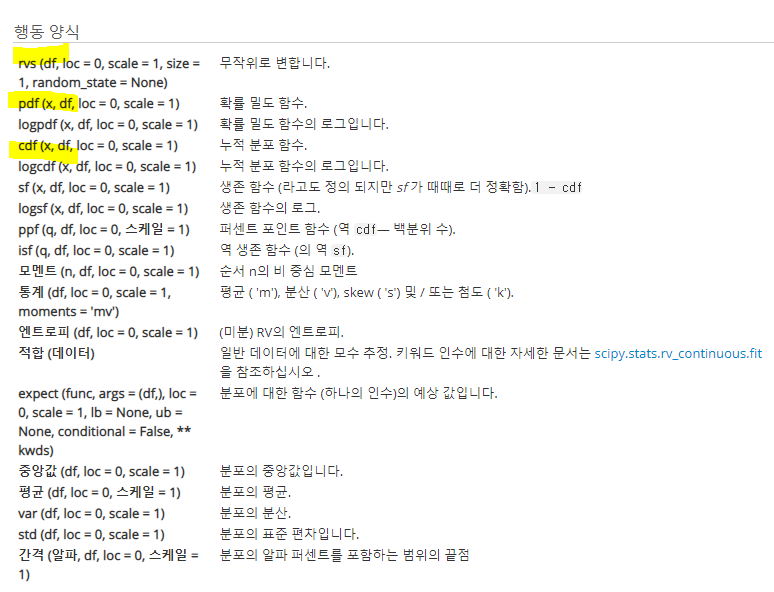
참고 : SciPy.org