통계

모집단과 모수 & 표본집단과 표본통계량

(Population, Parameter / Sample, Sample Statistic)

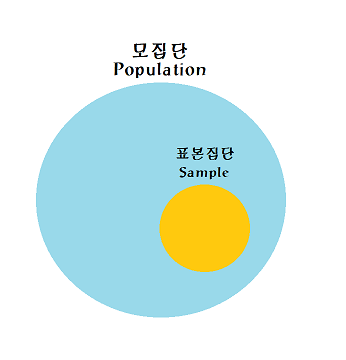
• 모집단 (Population)
  = 전체값
  = 평소에 잘 알수가 없음.
  = 전체 집단의 모든 데이터를 알지 못하더라도, 수학적으로 그 분포를 기술할 수 있는 특성값 (=모수)들을 안다면 추측가능함.

• 모수(Parameter)의 종류
  -평균
  -분산/표준편차
  -분위수(중위값,1분위수,4분위수 등)
  -모비율 등

• 표본집단 (Sample)
  = 모수를 추정하기 위해 모집단에서 추출한 샘플(일부)
  = 현실적으로 생각하면 모집단 전체에 대해 검사하기에는 비용이 너무 많이 들기 때문에 표본집단을 추출해 모수를 추정함
  = 표본은 여러개 가능
  = 그리고 매번 추출할 때마다 그 값이 달라짐. (표본집단을 100명중 15명으로 랜덤으로 뽑는다고 하면, 여러번 뽑을 때마다 매번 다른 15명이 뽑힐 것이다.)
  = 추출된 표본들에게서 표본 통계량을 구할 수 있음
  = 표본이 매번 추출할 때 마다 그 값이 변하는데, 표본 통계량도 역시나 매번 변함.
  (표본 통계량은 모수의 '추정(수)치'로 볼 수 있고, 추정된 값은 항상 오차를 수반함)

• 표본 통계량(sample statistic)의 종류
  -표본 평균
  -표본 표준편차
  -표본 비율
  -표준 오차
  (=표본 평균의 표준편차 = Standard Error of Mean(SEM))

헷갈리는 단어 주의

모수의 표준편차
표본통계량의 표준편차
표본통계량의 표본평균의 표준편차(=표준오차)