백준 14501

문제 설명

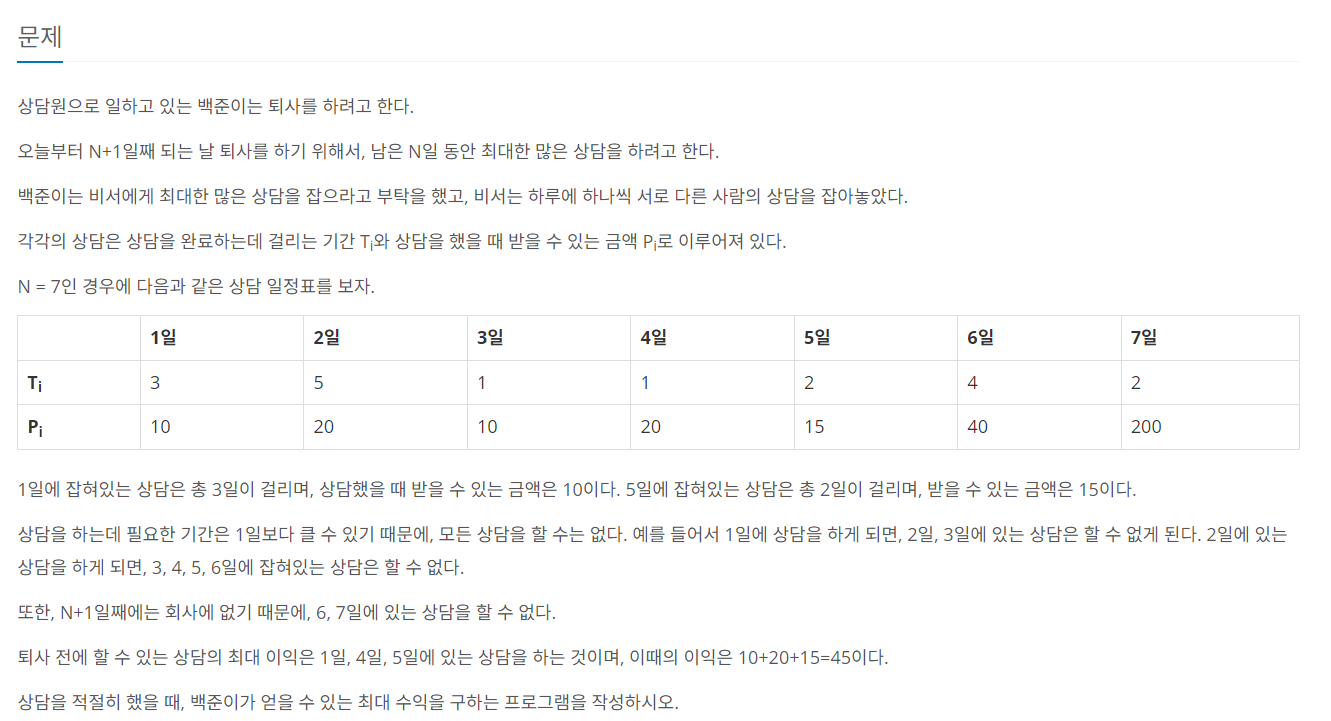
상담 일을 하며, 얻을 수 있는 최대 수익을 계산하는 문제다.

가능한 많은 일을 하는 게 항상 최선이 아닐 수 있다.

접근 방법

• i번째 일까지 일했을 때, 얻을 수 있는 최대 수익을 담기 위한 dp배열
• 배열의 가장 마지막 값이 답
• i번째까지 일했을 때 얻는 최대 수익을 계산
• j는 i번째 날에 상담을 진행했을 때, 상담이 가능한 모든 날짜,
  == i + i번째 날의 상담 기간부터 마지막날까지
• j를 기준으로 상담했을 때 얻는 최대 수익을 dp[j]에 저장

해결하지 못한 코드

import sys

input = sys.stdin.readline

n = int(input())

work = []

for i in range(n):
    time, price = map(int, input().split())
    work.append([time, price])

total_list = []

for i in range(n):
    total = 0
    
    while i < n:
        if i + work[i][0] > n:
            break

        total += work[i][1]
        i += work[i][0]
    
    total_list.append(total)

print(max(total_list))

그리디하게 접근하다가, 고려하지 못한 경우의 수가 생기는 것을 알았다.

해결한 코드

import sys

input = sys.stdin.readline

n = int(input())

work = []

for i in range(n):
    time, price = map(int, input().split())

    work.append([time, price])

dp = [0 for i in range(n+1)]

for i in range(n):
    for j in range(i + work[i][0], n+1):
        if dp[j] < dp[i] + work[i][1]:
            dp[j] = dp[i] + work[i][1]

print(dp[-1])

문제 해결 방법이 떠오르지 않아, 블로그를 참고했고, dp배열을 활용해 해결했다.