분할 정복

분할 정복도 이름에서 나는 어떤 알고리즘이다 라고 말하는 것처럼
이름만 봐도 어떤 방식으로 진행 될지 쉽게 유추할 수 있는 알고리즘이다.

주어진 문제를 둘 이상의 부분 문제로 나누고, 각 문제에 대한 답을 계산하고, 그 답을 이용해서 전체 문제의 답을 도출해내는 알고리즘이다.
물론 분할 정복을 사용하기 위해서는 문제에 몇가지 조건이 성립해야한다.

문제를 둘 이상의 부분 문제로 나누는 자연스러운 방법이 있을것
부분문제를 합쳐서 전체 문제의 답을 계산해내는 방법이 있을 것

이 같은 조건이 성립해야 분할 정복을 사용할 수 있다.

문제를 보면서 어떻게 구현하는지 알아보자.
boj 6549-히스토그램에서 가장 큰 직사각형
분할정복의 대표격 문제 중 하나인 문제로 설명해 보겠다.

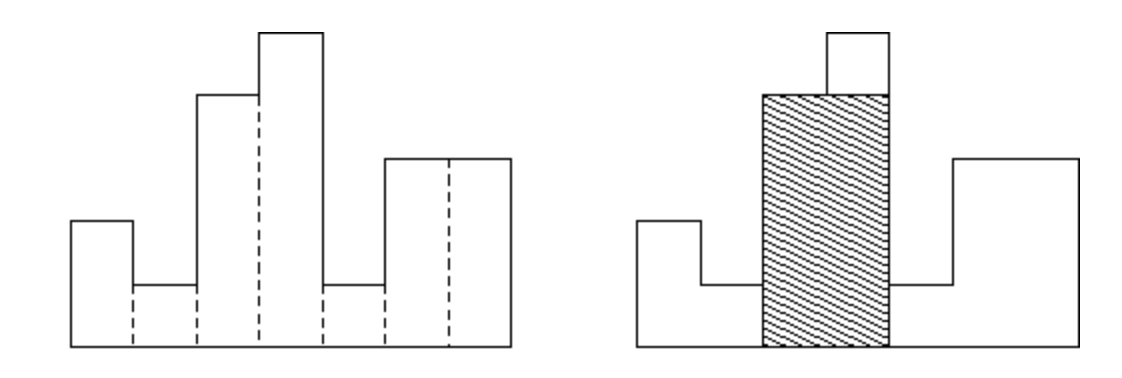
이런 히스토그램에서 어떻게 구성해야 가장 큰 크기의 사각형이 나오게 되는지 찾는 문제이다.
스택을 사용해서 푸는 방법도 있지만 여기선 분할 정복으로 푸는 법을 알아보자.

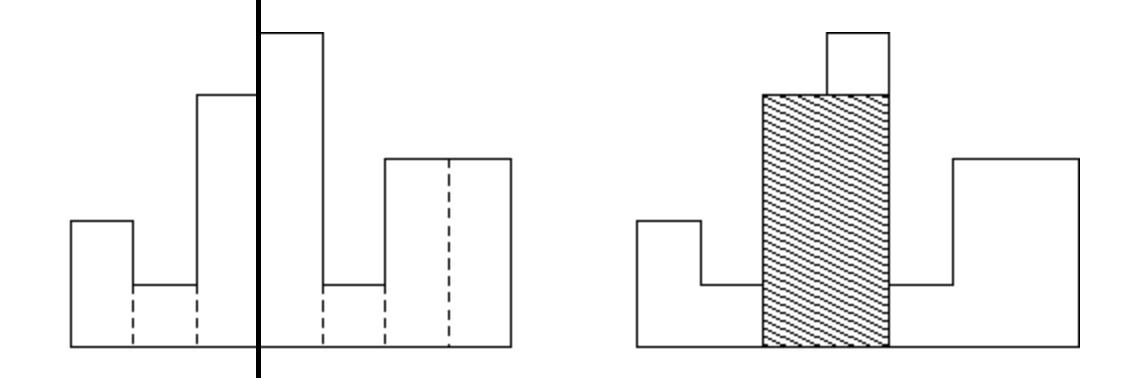
이런 식으로 먼저 반을 나눈다.
그러면 최대 직사각형은 다음 세가지 중 하나에 속하게 될 거다.

최대 직사각형은 왼쪽 부분에 존재한다.
최대 직사각형은 오른쪽 부분에 존재한다.
최대 직사각형은 왼쪽과 오른쪽에 걸쳐있다.

이 중에 단순히 오른쪽 왼쪽에 존재하는 부분은 그냥 처음에 분할한 부분을 재귀호출로 쉽게 구할 수 있다.
걸쳐있는 부분은 그 경계를 포함한 사각형을 오른쪽 한 칸 왼쪽 한칸 확장해가며 가장 큰 사각형을 찾을 수 있다.
구현한 코드로 마무리 하겠다.

vector<ll> h; //각 막대의 높이를 저장하는 벡터
ll solve(ll left, ll right){
    if(left == right) //분할을 끝낼 base case
        return h[left];
    //(left,mid)와 (mid + 1,right)로 분할 정복
    ll mid = (left + right)/2;
    ll ret = max(solve(left,mid), solve(mid + 1,right));
    //걸쳐있는 사각형 중 최대 찾기
    ll lo = mid, hi = mid + 1;
    ll height = min(h[lo],h[hi]);
    ret = max(ret, height * 2);
    //사각형이 입력 끝까지 커버하는 동안 반복
    while(left < lo || hi < right){
    	//항상 높이가 더 높은(넓이가 큰)방향으로 확장
        if(hi < right && (lo == left || h[lo-1] < h[hi+1])){
            hi++;
            height = min(height,h[hi]);
        }
        else{
            lo--;
            height = min(height, h[lo]);
        }
        ret = max(ret, height * (hi - lo + 1));
    }
    return ret;
}
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    while(1){
        h.clear();
        int n;
        cin >> n;
        if(n == 0)
            break;
        for(int i = 0; i < n; i++){
            int a;
            cin >> a;
            h.push_back(a);
        }
        cout << solve(0,n-1) << "\n";
    }

    return 0;
}