새해가 밝았습니다!
다들 새해복 많이 받으시고 하시는 일 다 잘되시길 기원합니다! 24년엔 코딩실력 많이 오르게 해주세요 ㅎㅎ...

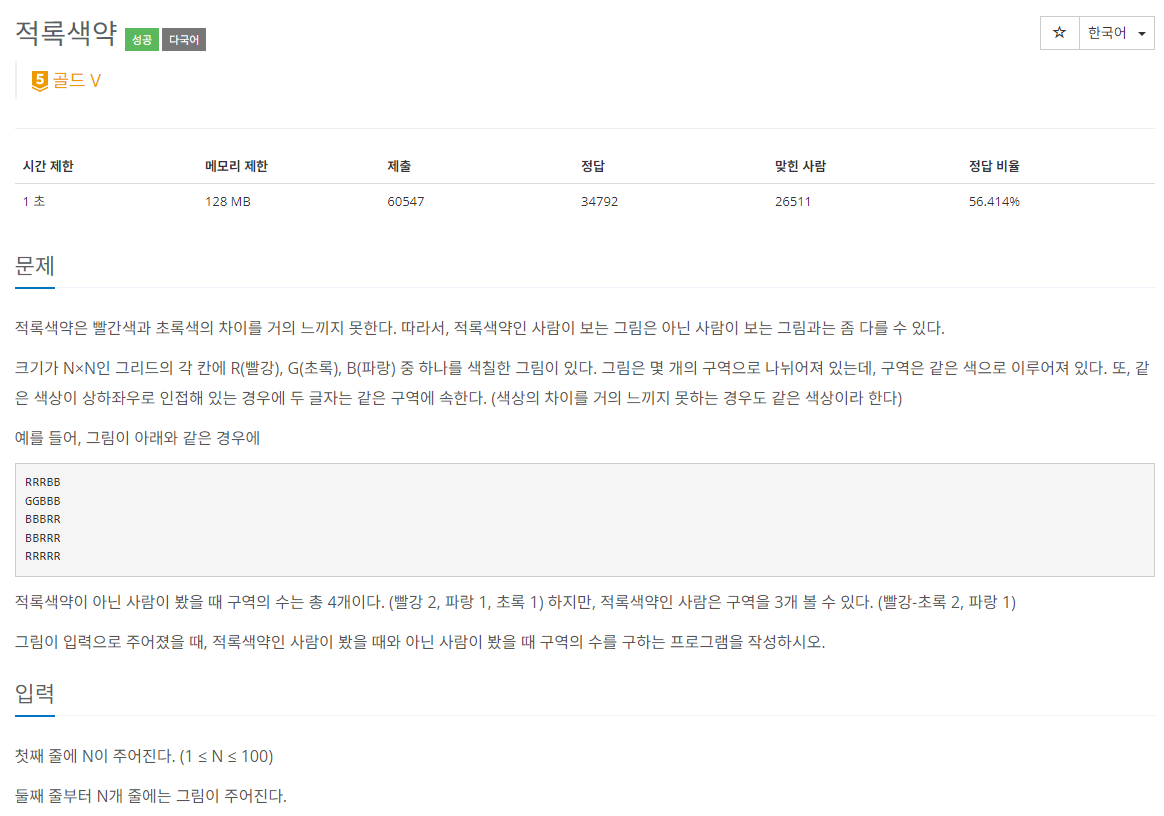
10026번 - 적록색약

위와같이 3색 배열 그림이 주어지면 구역(동일한 각 색깔이 뭉쳐있는 곳)이 총 몇 개인지 구하는 문제입니다.
단, 색약인 사람을 위해서 R과 G를 동일하게 취급하여 구한 결과 또한 출력해야 합니다.

세팅

from collections import deque
import copy
dx = [-1,1,0,0]
dy = [0,0,-1,1]

보자마자 BFS로 풀어야겠다고 생각했습니다.
항상 BFS 알고리즘을 사용하기 위한 기본적인 세팅, 상하좌우 선언과 que를 불러와줍니다.

N = int(input())
que = deque()
graph = []
for _ in range(N):
    graph.append(list(input()))
visited = [[0]*N for _ in range(N)]
graph_sakyak = copy.deepcopy(graph)

그림의 색 정보를 받아줄 graph 리스트를 하나 만들고 해당 인덱스를 방문했는지 표기해줄 visited 변수를 하나 만들어줍니다. 현재 초기값 graph와 동일한 graph_sakyak을 하나 만들어 나중에 색약인 그래프를 판별해주도록 합시다.

색약이 아닐 때

먼저 색약이 아닌 경우의 구역을 구해주도록 하겠습니다.

sum = 0
for i in range(N):
    for j in range(N):
        if not visited[i][j]:
            sum += 1
            bfs(i,j)

만약 해당 구역 방문을 안했으면 구역 방문 횟수(sum)을 높이고 해당 구역을 전부 탐색해주겠습니다.

        if graph_sakyak[i][j] == 'G':
            graph_sakyak[i][j] = 'R'

색약인 경우는 G가 R로 보이거나 R이 G로 보이기 떄문에 쓸데없는 for문 낭비를 줄이기 위해서 여기서 graph_sakyak에 R과 G를 동일하게 만들어 색맹 효과를 주겠습니다.

def bfs(x,y):
    que.append([x,y])
    while que:
        x,y = que.popleft()
        for i in range(4):
            nx = dx[i] + x
            ny = dy[i] + y
            if nx<0 or ny<0 or nx>=N or ny>=N:
                continue 

방문하지 않은 인덱스의 4방향 탐색을 돌아줍니다.

            if graph[x][y] == 'R' and graph[nx][ny] == 'R' and not visited[nx][ny]:
                visited[nx][ny] = 1
                que.append([nx,ny])
            if graph[x][y] == 'G' and graph[nx][ny] == 'G' and not visited[nx][ny]:
                visited[nx][ny] = 1
                que.append([nx,ny])
            if graph[x][y] == 'B' and graph[nx][ny] == 'B' and not visited[nx][ny]:
                visited[nx][ny] = 1
                que.append([nx,ny])

만약 자기 자신이 해당 색깔이고 그 다음 나올 것도 해당 색깔이면 그건 곧 구역이 형성되므로 방문 여부를 표시해주고 다음 나올 인덱스도 탐색에 넣어주도록 합시다.

자기 자신이 if문 조건에 들어간다면 R->R 탐색만 가능해 R->B 또는 R->G와 같이 탐색하는 경우를 없애 해당 구역만 탐색이 가능합니다.

색약일 때

색약일 때는 아까 만들어준 graph_sakyak을 graph에 덧씌워서 다시 bfs 탐색을 돌리면 됩니다.

visited = [[0]*N for _ in range(N)]
graph = graph_sakyak[:]
sum2 = 0

이런씩으로요.
참고로 graph_sakyak을 만들 때랑 graph에 덧씌울때랑 복제 방법이 다른 이유는 shallow copy랑 deep copy 기법 때문에 그렇습니다. 깊은 복사를 하지 않으면 원본 배열에 영향을 받아서 리스트가 오염될 수 있습니다.

for k in range(N):
    for p in range(N):
        if not visited[k][p]:
            sum2 += 1
            bfs(k,p)

방금 말씀드렸듯이 graph_sakyak을 덧씌운 graph를 다시 한번 BFS를 돌려주도록 합시다.

print(sum,sum2)

마지막으로 구역 합산한 결과를 출력해주면 정상적으로 답을 도출할 수 있습니다.