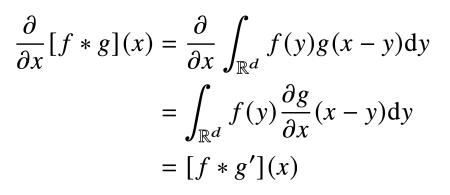CNN

중요개념

• Convolution 연산
• 역전파

목표

Convolution 연산은 오늘날 굉장히 많은 모델에서 이미지나 영상을 처리하기 위해 사용됩니다. 지금까지 배웠던 fully connected layer와 비교해서 CNN(Convolutional Neural Network)의 커널 연산이 가지는 장점과, Convolution 연산이 다양한 차원에서 어떻게 진행되는지를 이해하고 넘어가자.

권고사항

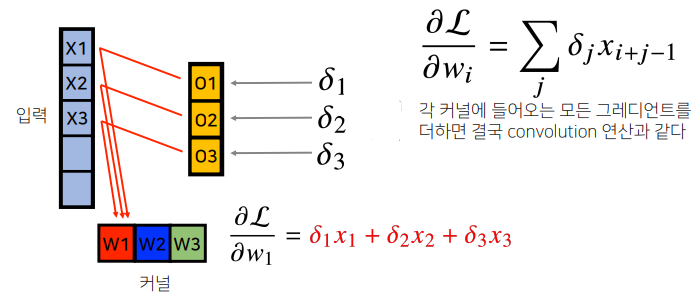
Convolution 연산의 경우, 커널의 모든 입력데이터에 대해 공통으로 적용이 되기 때문에 역전파를 계산하는 경우에도 똑같이 Convolution 연산이 나오게 됩니다. 강의에서 그림과 함께 잘 설명되어 있기 때문에 커널을 통해 그레디언트가 어떻게 전달이 되는지, 역전파가 어떻게 이루어지는지 꼭 짚고 넘어갑시다.

Convolution 연산 이해하기

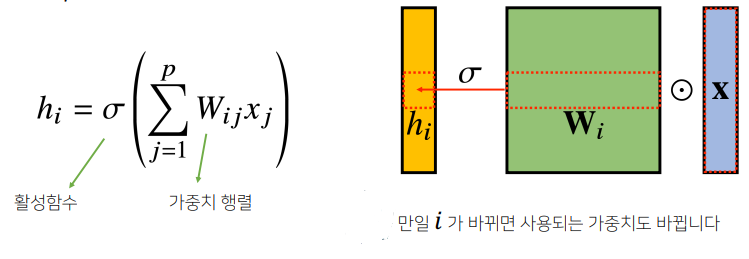
• 지금까지 배운 다층신경망(MLP)은 각 뉴런들이 선형모델과 활성함수로 모두 연결된 (fully-connected) 구조였습니다.
  

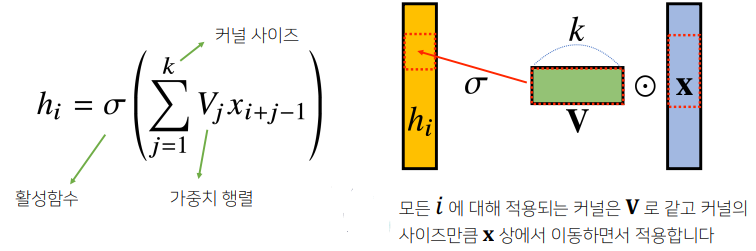
• Convolution 연산은 이와 달리 커널(Kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다.
  - 활성화함수를 제외한 Convolution 연산도 선형변환에 속합니다.
  

• Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것입니다.
  

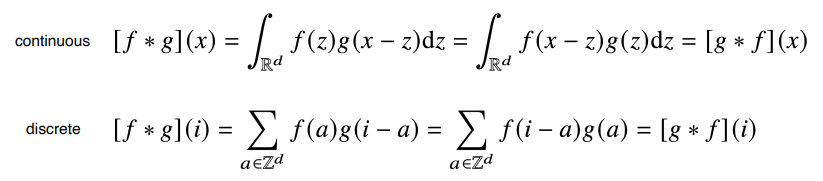
• 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용합니다.

• Convolution 연산은 1차원 뿐만 아니라 다양한 차원에서 계산 가능합니다.
  

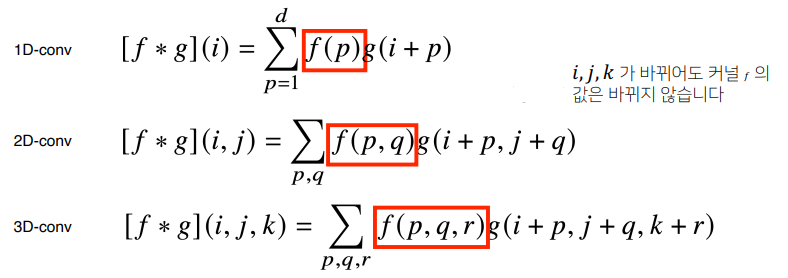
• 2D-Conv 연산은 이와 달리 커널(Kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다.

• 입력 크기를 (H,W), 커널 크기를 (KH,KW), 출력 크기를 (OH,OW)라 하면 출력 크기는 다음과 같이 계산합니다.
  

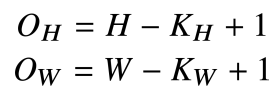
• 채널이 여러 개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다고 생각하면 됩니다.
  

• Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 Convolution연산이 나오게 됩니다.