DFS와 백트래킹 : 유사하지만 다른 탐색 알고리즘

호기성세균·2023년 6월 16일

cs

목록 보기

27/29

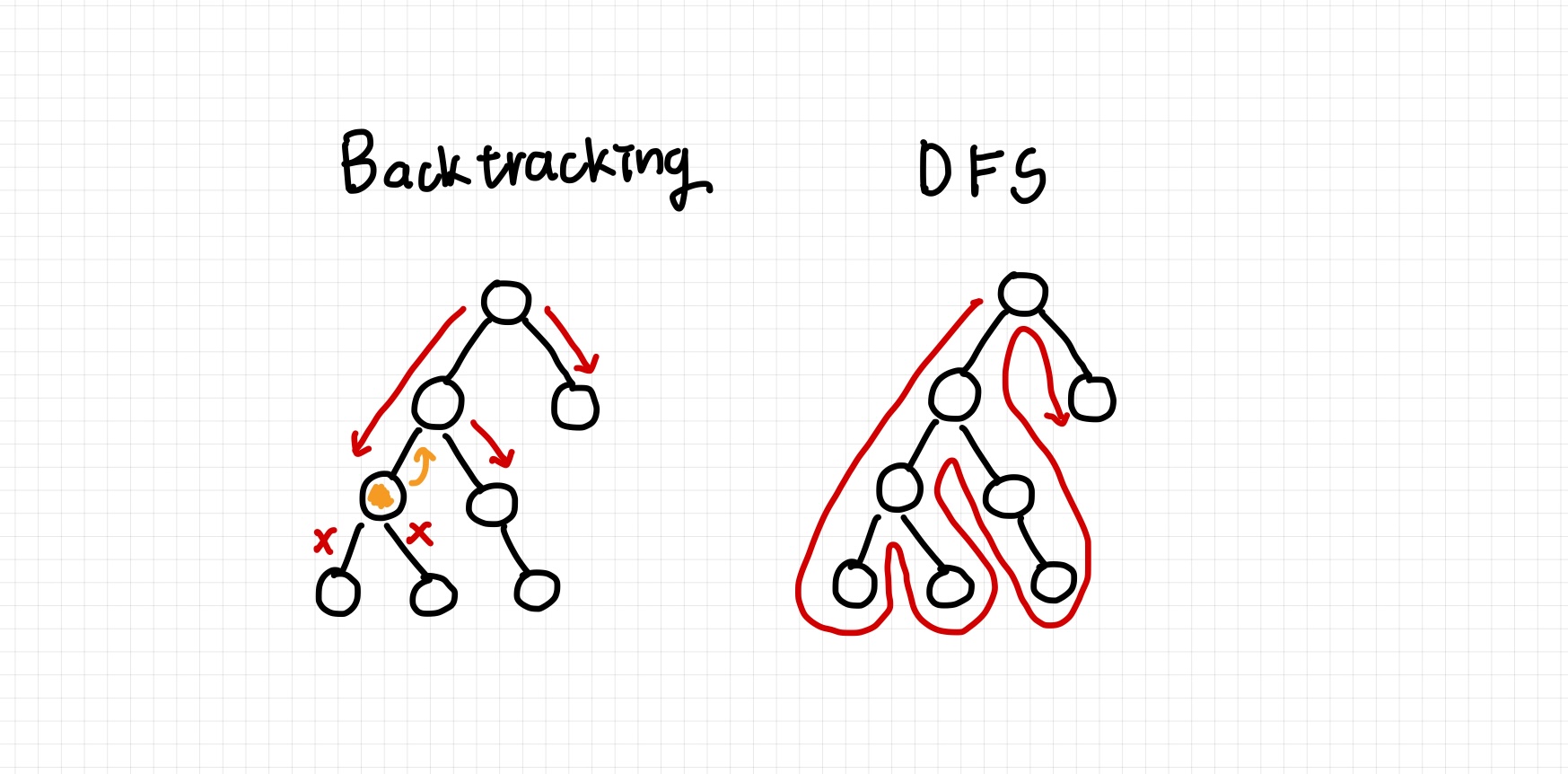
알고리즘 문제를 풀다 보면 백트래킹과 DFS 알고리즘이 매우 유사하게 느껴질 때가 많다.
실제로, 많은 문제가 DFS로 해결되면 백트래킹으로도 해결될 수 있는 경우가 많은 것을 경험했을 것이다.
하지만 과연 두 알고리즘은 동일할까?
두 알고리즘이 어떻게 다르고, 어떤 차이점이 있는지 알아보자.

[Backtracking(백트래킹)이란?]

탐색 알고리즘 중 하나로, 현재 상태에서 가능한 모든 경로를 따라 들어가며 해를 찾는다.
단, 탐색 중 불필요하거나 유효하지 않은 경로를 발견하면 즉시 탐색을 멈추고 이전 단계로 되돌아가(back) 다시 탐색을 이어간다.

[동작 방식]

백트래킹은 재귀를 사용하여 탐색을 진행하며, DFS 방식에 기반을 둔 탐색 방법이다.
❗️ 하지만 핵심 차이는 조건에 맞지 않는 경로는 더 이상 탐색하지 않고 조기에 가지치기를 한다는 점이다.

[예시 : 백트래킹을 이용한 순열 생성]

// 백트래킹을 이용한 순열 생성
void backTracking(int depth) {
    if (depth == M) {
        printAnswer();
        return;
    }
    for (int i = 1; i <= N; i++) {
        if (!visited[i]) {  // 조건 확인
            visited[i] = true;
            answer[depth] = i;
            backTracking(depth + 1);  // 더 깊이 탐색
            visited[i] = false;       // 백트래킹: 상태 복구
        }
    }
}

위 코드에서 보듯이, 탐색 도중 조건을 만족하지 않는 경우(if (!visited[i]) 조건)에만 깊이 탐색을 진행하며, 조건이 맞지 않으면 더 이상 진행하지 않고 돌아온다.

[DFS(Depth-First Search)란?]

그래프나 트리와 같은 자료 구조에서 노드를 탐색하는 기본적인 알고리즘이다. 이름 그대로, 깊이 우선으로 탐색하며 한 경로를 끝까지 탐색한 후 더 이상 갈 곳이 없으면 이전 경로로 돌아가 다른 경로를 탐색한다.

[동작 방식]

재귀나 스택을 사용하여 구현되며, 모든 경로를 탐색하는 데 사용된다.
❗️ 백트래킹처럼 중간에 가지치기를 하지 않기 때문에, 조건을 만족하지 않는 경우에도 경로의 끝까지 탐색한다.

[예시 : DFS를 이용한 그래프 탐색]

void dfs(int node) {
    visited[node] = true;
    System.out.print(node + " ");

    for (int next : graph[node]) {
        if (!visited[next]) {
            dfs(next);
        }
    }
}

이 코드는 간단한 DFS 알고리즘으로, 모든 노드를 순차적으로 방문하고 탐색이 끝나면 이전 노드로 돌아간다. (조건 없이 모든 경로를 끝까지 탐색)

⭐️ DFS와 백트래킹의 차이점 ⭐️

1. 탐색 목적

DFS: 주로 모든 노드를 탐색하거나 경로를 찾는 것이 목적
(ex. 그래프의 모든 노드를 방문 / 경로가 존재하는지 확인)
백트래킹: 해를 찾는 과정에서 조건을 만족하지 않는 경로를 조기에 중단하여 탐색 효율을 높임
(ex. 최적화된 경로나 특정 조건을 만족하는 해를 찾기)

2. 조건 검증 (가지치기)

DFS: 별도의 조건 검사를 하지 않음.
백트래킹: 탐색 도중 조건에 맞지 않으면 즉시 중단하고 이전 단계로 돌아감

3. 탐색 종료 시점

DFS: 모든 경로를 탐색할 때까지 계속 탐색을 진행
(ex. 경로가 존재하는지 or 모든 노드를 방문할 때까지 진행)
백트래킹: 조건에 맞지 않는 경로는 탐색을 조기에 중단하고, 유효한 해를 찾으면 더 이상 탐색을 진행하지 않음
(ex. 조건을 만족하는 해를 찾으면 탐색을 종료)