시간복잡도
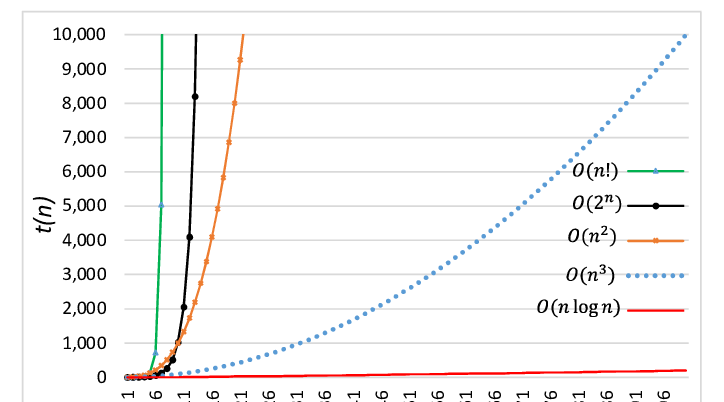
입력값에 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 걸리는 시간을 나타낸 것을 시간복잡도라 합니다.
빅오표기법
Big-O(빅-오)
Big-Ω(빅-오메가)
Big-θ(빅-세타)
빅오표기법은 시간복잡도를 표현하는 방법입니다.
각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법입니다.
일반적으로 시간복잡도를 표현할때 빅오표기법으로 나타냅니다.
O(1)
O(1)는 입력값이 아무리 증가해도 시간이 늘어나지 않는 경우입니다.
배열의 길이가 아무리 길어도 해당하는 인덱스에 접근하는 시간은 동일합니다.
function O_1 (arr, index) {
return arr[index];
}
let arr = [1,2,3,4,5];
let index = 1;
let result = O_1(arr, index);
console.log(result); // 2O(n)
O(n)는 입력값에 따라 시간이 같은 비율로 증가하는 경우입니다.
입력값이 1일때 1초의 시간이 걸리면, 입력값이 100일때 100초의 시간이 걸립니다.
function O_n(n) {
for (let i = 0; i < n; i++) {
// do something
}
}
function another_O_n(n) {
for (let i = 0; i < 2n; i++) {
// do something
}
}위의 알고리즘은 O_N(n)에서 n의 시간이 걸리고 another_O_n(n)에서 2n의 시간이 걸립니다.
따라서 총 3n의 걸리지만 빅오표기법에서는 계수의 크기에 상관없이 O(n)으로 표현합니다.
마찬가지로 다른 알고리즘이 추가되어서 3n + 1 같은 시간이 걸리다고 할지라도 상수를 무시하고
O(n)로 표현합니다.
O(log n)
입력값에 따라 log n 만큼 시간이 증가하는 경우입니다.
log n 이기 때문에 O(n) 보다 빠릅니다.(알고리즘 연산이 효율적입니다.)
log n의 시간복잡도를 가지는 알고리즘으로는 BST(이진 탐색 트리)가 있습니다.
O(n^2)
입력값에 따라 n^2 만큼 시간이 증가하는 경우입니다.
2중 for문, 3중 for문을 사용하는 알고리즘이 O(n^2)에 해당합니다.
n^3 n^4 n^5 같은 경우도 전부 빅오표기법에서는 O(n^2)로 표현합니다.
function algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for(let k = 0; k < n; k++){
// do something
}
}
}
}O(2^n)
빅오표기법중 가장 느린 시간복잡도 입니다.
재귀를 이용한 연산들이 이에 해당합니다.
굉장히 비효율적이기 때문에 다른 방식을 고민하는것이 좋습니다.
fucntion fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}시간복잡도의 법칙
계수 법칙
상수 k가 0보다 클 때 f(n) = O(g(n))이면 kf(n) = O(g(n))이다.
n이 무한에 가까울수록 k의 크기는 의미가 없기 때문이다.
-> 시간복잡도의 계수는 생략한다.
for (let i = 0;i < n;i += 1){
// ...
}
for( let i = 0;i < n *5; i+= 1){
// ...
}곱의 법칙
f(n) = O(h(n))이고 g(n) = O(p(n))이면 f(n) g(n) = O(h(n)) O(p(n))이다.
빅오는 곱해질 수 있다.
for (let i = 0; i< n; i +=1){
for (let i = 0; i< m * 5; i += 1){
// ...
}
} 다항 법칙
f(n)이 k차 다항식이면 f(n)은 O(n^k)이다.
for(let i = 0; i < n * n *n; i+=1){
// ...
}코딩테스트를 위해 두가지만 기억하세요
- 상수항은 무시
- 가장 큰 항 외엔 무시
성능 측정 방법
Date 객체를 이용
const start = new Date().getTime();
// ...
const end = new Date().getTime();
console.log(end - start);