#5 딥러닝

👍 퍼셉트론을 여러개 사용하여 보다 복잡한 결정 경계에서도 적용이 가능한 MPL의 학습 방법인 오류 역전파에 의해서 인공신경망에 대한 관심은 높아졌다 ❗❗

인공 신경망에서 딥러닝으로 발전하게 된 원인은 바로 MLP의 학습 성능 때문 😨 ❓

• 이전의 다층 퍼셉트론의 경우에는 층의 개수를 2~3 정도로 하여 학습을 하였는데, 학습이 잘 되었다.

• 하지만 층의 개수를 얕게 하여 학습하는 것에는 한계가 존재했고 층의 개수를 늘리면 늘릴수록 학습이 잘 되지 않았다 💦

해당 문제의 원인은 기울기 손실의 문제였던 것 ❗❗

✔️ 기울기 소실 문제

• 기울기 소실의 문제점이 생긴 이유는 MLP의 학습 방법의 문제였는데, 다층 퍼셉트론의 학습 방법은 오류 역전파를 이용하는것이었다.

• 오류 역전파는 경사하강법을 기반으로 학습을 시키는데, 이때 미분된 값이 사용이 된다.

• 경사 하강법은 현재 파라미터에 미분된 값을 곱해주게 되는데, 퍼셉트론의 경우에는 활성 함수를 사용하여 출력값을 결정한다.

• 그래서 처음에는 충부한 값을 가지나, 계속해서 미분된 값을 곱해줌으로써 '0'에 가까운 값을 가지게 되면서 기울기 소실의 문제점이 발생하게 된 것 😮😮

✔️ 기울기 소실 해결 : 활성 함수 변경 🧡

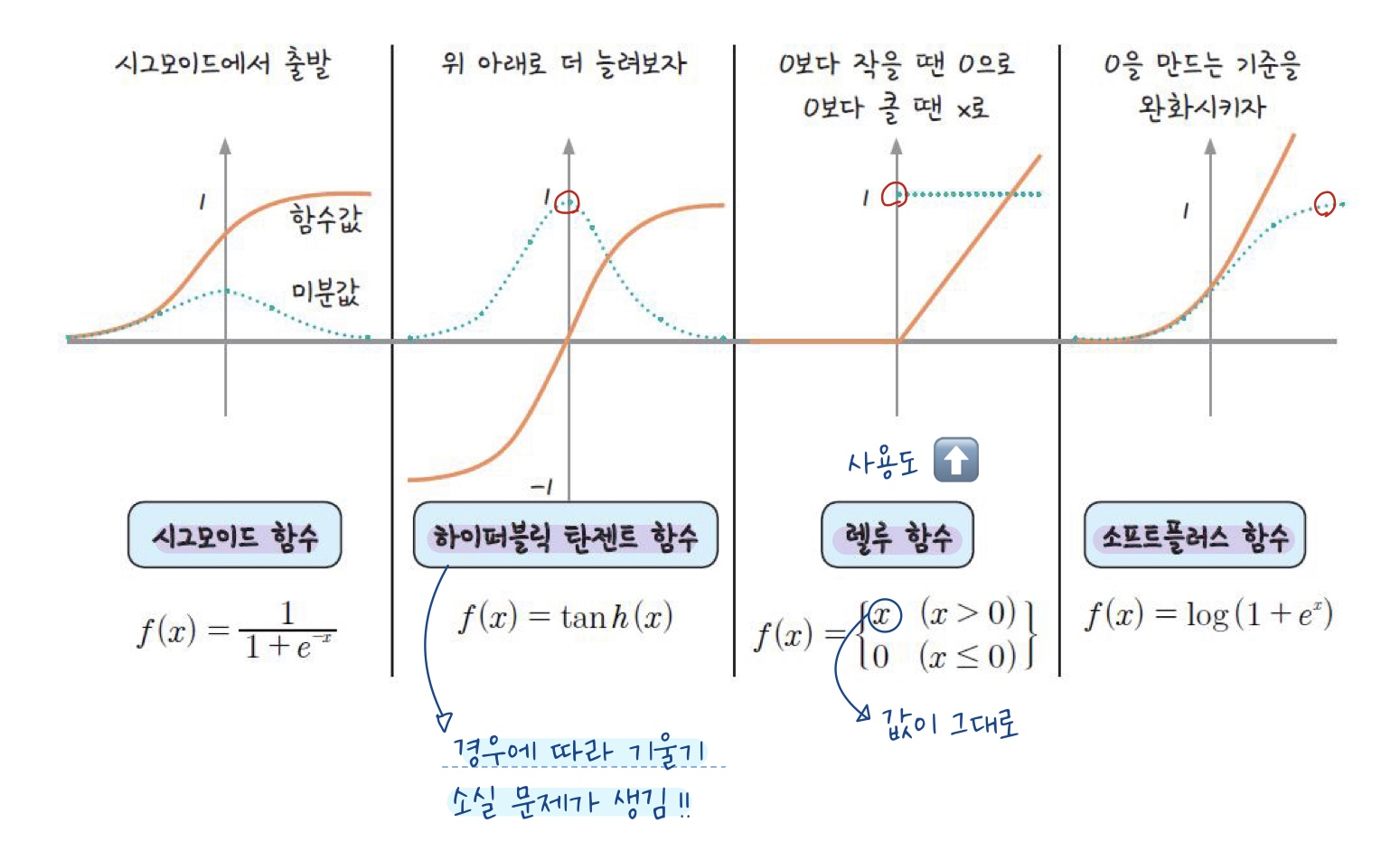
• 본래 사용하던 시그모이드의 경우에는 미분을 적용하게 되면 최대 0.3의 값을 가지게된다.

• 따라서 미분을 하더라도 값이 많이 작아 지지 않는 활성 함수를 사용하여 기울기 소실 문제를 해결하면서 깊게 층을 쌓아도 학습이 가능해지게 되었다 😭👍

💚새로운 활성 함수💚 : 미분을 하더라도 비교적 큰 값을 지닌다 ❗

✔️ 그 외 딥러닝 성능을 높이기 위한 제안

1. 가중치를 임의의 값으로 초기화 하지말고 조금 더 선명한 값을 사용하자는 것

2. 딥러닝의 경우층을 많이 쌓을 수록 학습이 더 잘 된다는 것

✔️ 다양한 층을 사용할 경우의 특징

• 딥러닝의 가장 큰 특징 중 하나는 특징 설계를 하지 않아도 된다는 것이었다 👍

• 기존의 기계학습의 경우 특징 추출을 위해 사람이 직접적으로 특징을 설계해야 했지만, 딥러닝의 경우에는 학습 과정에 특징 추출이 포함되어있어 특징 설계가 필요없다는 것이다.

• 딥러닝의 경우에는 각 층에서나오는 결과값이 다르다 ❗❗

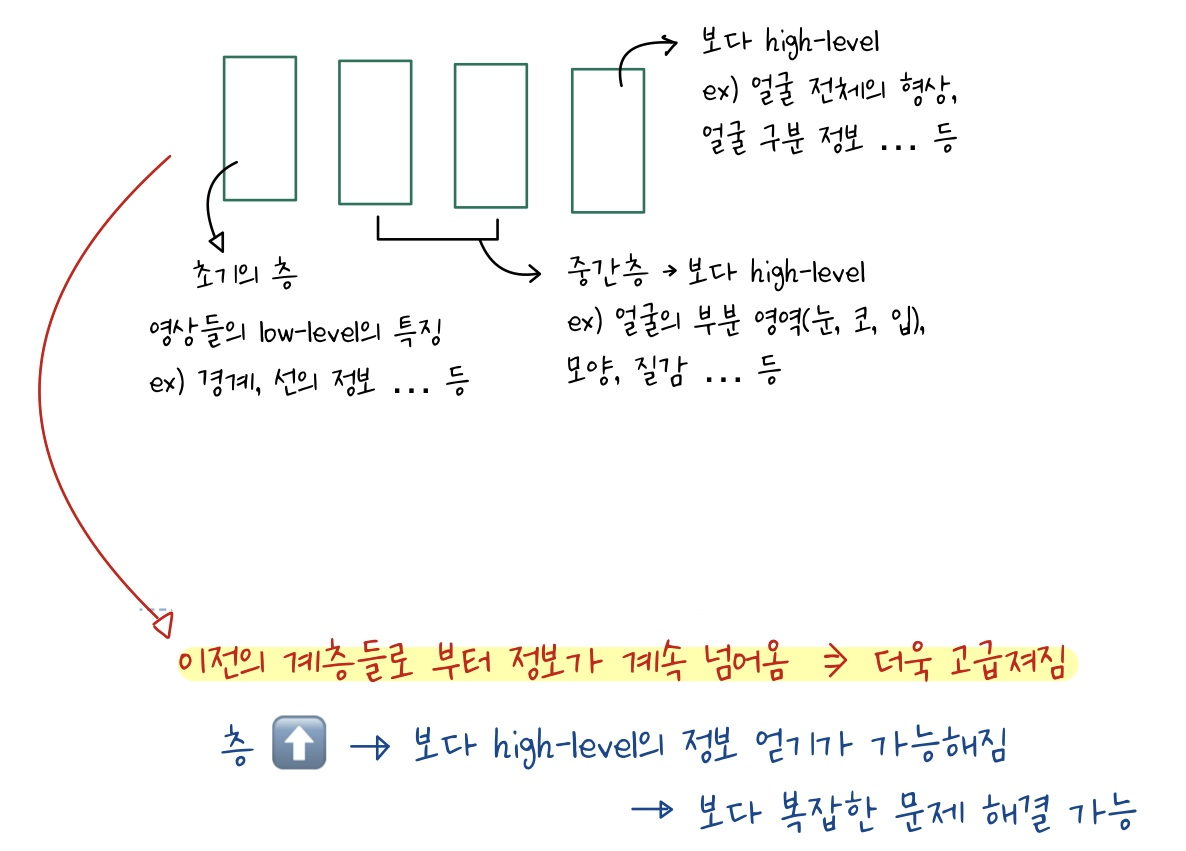
• 딥러닝에서 찾아내는 특징들은 각 구성한 네트워크 계층에 따라 다르게 나타나는 것 🙄🙄

• 입력층과 가까운 층의 결과값은 보다 low-level의 특징을 가지게 되고 출력 층과 가까운 층의 경우에는 보다 high-level의 특징을 가지게 된다.

• 이러한 형태를 띄게 된 이유는 이전층의 출력값이 다음층으로 전달이 되기 때문에 점차 고급진 정보를 가질 수 있게 되는 것이다 👍