Dynamic Programming

✅ Dynamic Programming(동적 계획법)

• 메모리 공간을 약간 더 사용하면 연산 속도를 비약적으로 증가시킬 수 있는 방법

• 큰 의미에서 분할 정복과 같은 접근 방식을 의미함 ➡ 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법

• 분할 정복과는 나누는 방식에서 차이점이 생기는데 동적 계획법 같은 경우에는 한 번만 계산하고 그 결과를 다른 문제에도 계속해서 계산 결과를 재활용하여 적용 ➡ 문제들이 서로 영향을 미침

• 두번 이상 반복 계산 되는 부분 문제들의 답을 미리 저장함으로써 속도의 향상을 꾀하는 알고리즘 설계법

▶ 예제

출처 https://rh-tn.tistory.com/32

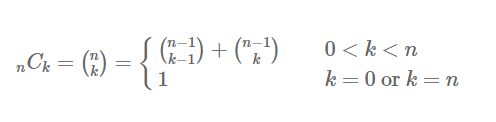
💨 구상

• 재귀 호출을 이용한 이항계수 계산

def bino(int n, int r) :
   if r == 0 or n == r :
   	return 1
   return binot(n-1, r-1) + bino(n-1, r)

<문제점> n과 r이 커짐에 따라 함수의 중복 호출이 기하급수적으로 늘어남 + 수행시간

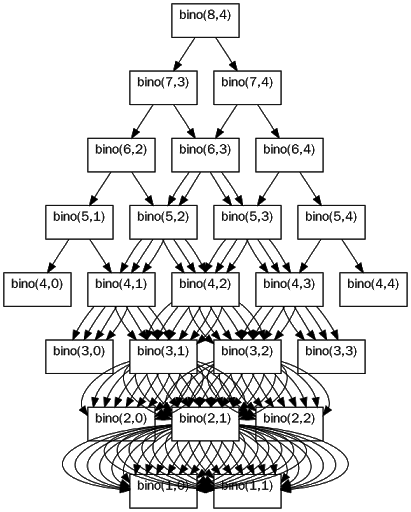
시간 복잡도 : O(2^N)

🔔 해결 방안 - 다이나믹 프로그래밍

• 적용 가능한 경우
  1 큰 문제를 작은 문제로 나눌 수 있는 경우
  2 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제도 동일한 경우

🔔 메모이제이션 => 캐싱

• 함수의 결과를 저장하는 장소를 마련해 두고 한 번 계산한 값을 저장 해뒀다 재활용하는 최적화 기법

• 모든 부분 문제가 한 번씩만 계산된다노 보장 ➡ 함수 호출 횟수 급격한 감소

cache = [[0]*2]*100

def bino2(int n, int r) :
    if r == 0 or n == r: 
    	return 1;
        
    if cache[n][r] != 0:
        return cache[n][r]
    
    cache[n][r] = binot(n-1, r-1) + bino(n-1, r);
    return cache[n][r]

➰ 메모이제이션 적용 방법

1 기저 사례를 먼저 처리함
2 함수의 반환값이 항상 0이라는 점을 이용해 cache[]를 모두 -1로 초기화
3 참조를 이용하여 cache이용

➰ 탑 다운 방식

• 재귀 함수를 이용하여 다이나믹 프로그래밍 소스코드를 작성하는 방법

• 메모이제이션과 같은 것 !!!!!!!

• 사용되는 결과 저장용 리스트를 'DP 테이블'이라고 부름