Greedy Algorithms

✅ Greedy Algorithms(탐욕법, 탐욕 알고리즘)

• 문제를 해결하는 과정에서 그 순간순간마다 최적이라고 생각되는 결정을 하는 방식으로 진행하여 최종 해답에 도달하는 문제 해결 방식

• 동적 프로그래밍 사용 시 지나치게 많은 일을 한다는 것에서 착안하여 고안된 알고리즘

• 꼭 정답을 내는 것이 아니라서 프로그래밍 대회에서는 대개 발목을 잡기도 함

• 문제에서 '큰 순서대로', '작은 순서대로' 등 기준 제시 => 정렬 알고리즘과 짝을 이루어 출제될 가능성 높음

💫 사용되는 경우

1 탐욕법을 사용해도 항상 최적해를 구할 수있는 문제를 만난 경우, 탐욕법은 동적 계획법보다 수행 시간이 훨씬 빠르기 때문에 유용

2 시간이나 공간적 제약으로 인해 다른 방법으로 최적해를 찾기 너무 어렵다면 최적해 대신 적당히 괜찮은 근사해를 찾는 것으로 타협할 수 있음. 탐욕법은 이럴때 최적은 아니지만 임의의 답보다는 좋은 답을 구하는 용도로 유용함.

▶ 예제

출처 https://blog.naver.com/thdgksqls369/222211817166

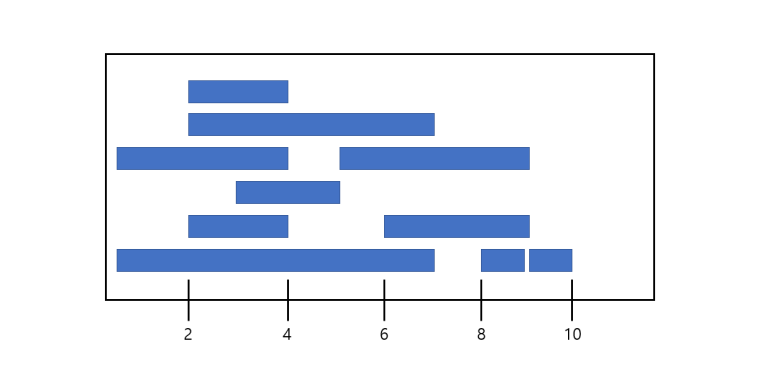
❓ 회의하고 싶은 시간을 제출한 인데 회의실이 하나 밖에 없음. 이 중 서로 겹치치 않는 회의들만 골라서 진행하려 한다면 최대 몇개 선택을 할까?

💨 구상

• 첫번째 구상

  길이가 짧은 회의부터 하나씩 순회하면서 겹치지 않는 것을 들 추가하는 방법

  <문제점> 긴 회의 두개와 짧은 회의 하나가 겹친다면 긴 회의 두개 대신 짧은 회의 하나만을 개최함

• 두번째 구상

  길이와 상관없이 먼저 끝나는 회의부터 선택하는 방법

🔔 정당성 증명 : 탐욕적 선택 속성

• 탐욕적 선택 속성은 모든 부분을 고려하지 않고 탐욕적으로만 선택하더라도 최적해를 구할 수 있다는 것

• 어떤 알고리즘에 이 속성이 성립할 경우, 우리가 각 단계에서 탐욕적으로 내리는 선택은 항상 최적해로 가는 길 중 하나

🔔 정당성 증명 : 최적 부분 구조

• 첫번째 선택을 하고 나서 남는 부분 문제는 쵲거이 아닌 방법으로 풀어야 하는 경우

• 부분 문제의 최적해에서 전체 문제의 최적해를 만들 수 있음을 보여야함

• ex) 첫번째 회의를 잘 선태갈고 겹치는 회의를 모두 걸러냈다면, 남은 회의 중에 최대한 많은 회의를 선택하는 것