조이스틱
오락실 게임을 하다보면 이름을 조이스틱으로 입력하게 된다. 조작 횟수의 최솟값을 구해보자.
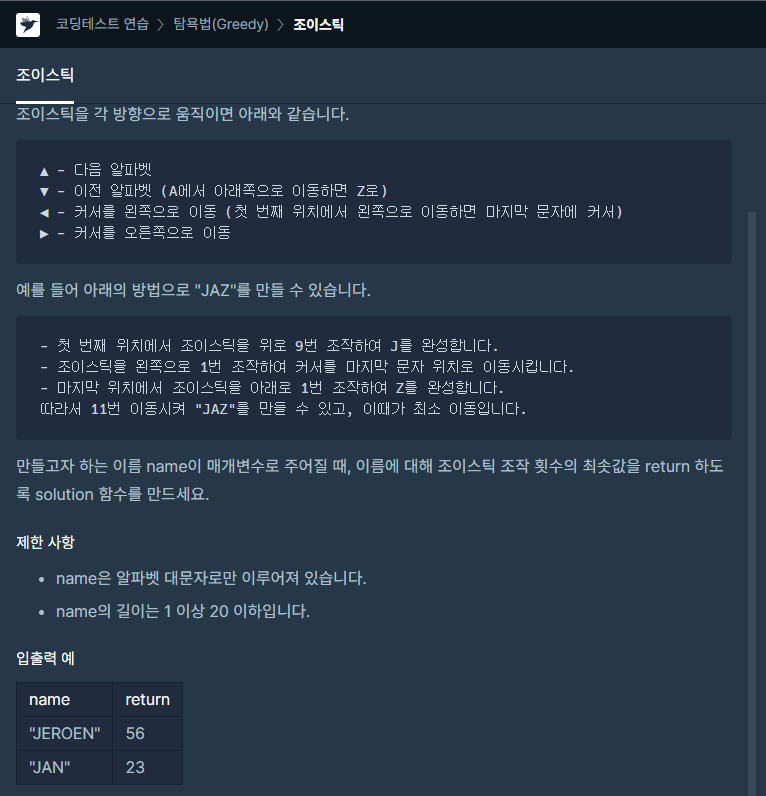
구현 아이디어
- 왼쪽 끝에서 오른쪽 끝으로, 또한 그 반대로도 1조작에 이동한다.
- 알파벳의 경우, Z에 가깝다면 A에서 Z로 1 조작에 이동한다.
- 양 끝에 가까운 연속된 A 가 미치는 영향을 생각한다.
구현
-
입력에 A가 존재하지 않는다면, 모든 자리를 알맞는 문자로 고치고, 모든 자리를 순회해야 하므로 총 조작 횟수는 이동 조작의 합 + 문자 변경 조작의 합이다.
-
문자 변경 조작: A의 아스키 코드를 ord로 구하고, ASCII_A에 저장한다. 입력의 각 알파벳에 대해, A와의 아스키 코드 차이를 구해 difference로 저장한다. 이때, 차이가 13 초과 나게 된다면 Z에서 접근하는 것이 최적이다. A와 Z는 1 조작 거리이고, Z에서 변경하는 데 필요한 조작은
ord("Z") - ord(char)이므로,1 + (ord("A") + 25) - ord(char) = 26 - difference로 정리할 수 있다.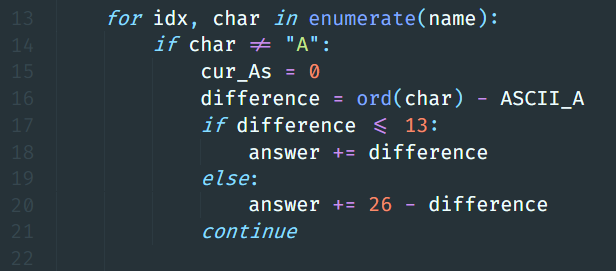
- 연속된 A 찾기 (최대 길이, 우측 끝)
- A를 찾게 되면
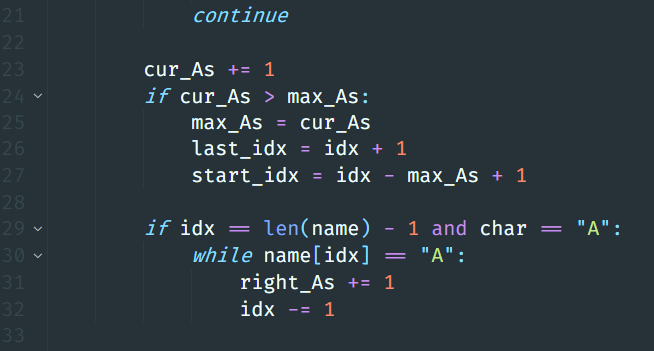
continue하단의 코드가 작동한다. A가 아닌 경우 0으로 초기화되던cur_As에 값을 하나씩 더한다. max_As를 업데이트하게 되면, 가장 긴 A 묶음의 시작과 끝 index를start_idx, last_idx로 지정한다. (name[start_idx: last_idx] =="AAA..AA") - 가장 우측의 문자가 A라면,
idx를 하나씩 줄여나가 A가 아닐 때까지 반복하여 우측의 A 묶음의 크기를right_As에 저장한다
- 이동 조작
본 문제의 핵심이다. 처음 시작 커서의 위치는 가장 좌측에 있는 문자를 변경할 수 있다. 해당 위치에서 최소한의 조작으로 변경이 필요한 모든 자리에 가려고 한다. 전략은 총 3가지이다.
- 돌아가기 (BAAAAAABBBB)
- 뚫고가기 (BBBBAABBBAA)
- 전부순회 (COMPUTER)
돌아가기
A의 묶음 중 가장 큰(A의 연속이 긴) 묶음의 크기 max_As가 크다면, 그 묶음을 뚫고 가는 대신 좌측 끝이나 우측 끝을 이용하여 반대로 이동하는 전략을 택한다.
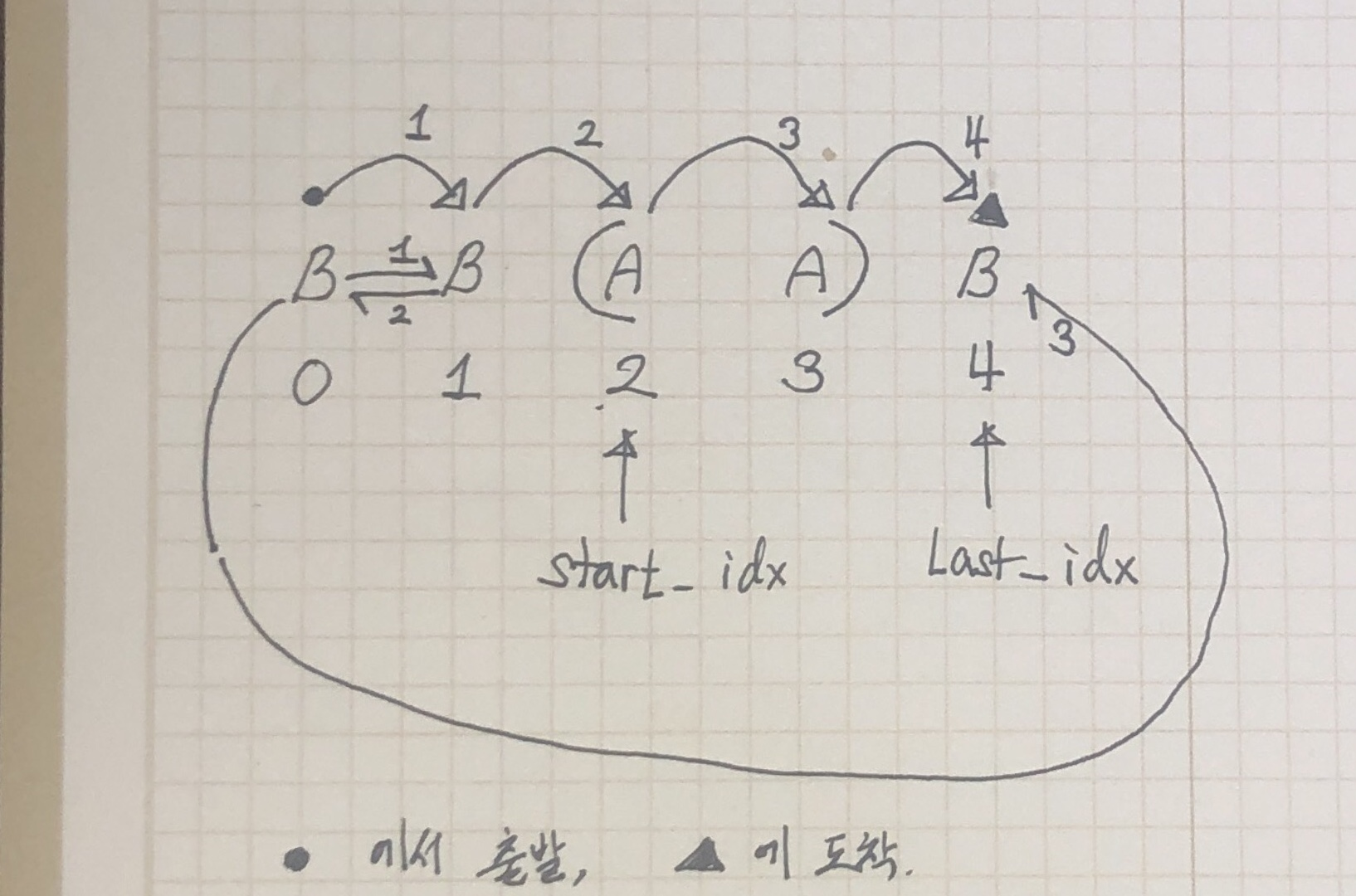
위의 상황에서 뚤고 간다면 이동에 4가 필요하고, 돌아간다면 3만 필요하다. 초기 위치로 돌아가는데 start_idx -1의 조작이 추가된 것이다(좌측을 향하는 2번 화살표). 따라서 max_As > start_idx일 때, 돌아가기가 유리하다. 오른쪽 끝에 대해서도 같은 논리를 적용하면, max_As > len(name) - last_idx일 때 돌아가기가 유리하다.
초기 위치에서 start_idx직전까지 이동할 때 필요한 횟수를 move_1, 초기 위치에서 last_idx로 이동할 때 필요한 횟수를 move_2로 저장한다. 돌아가기의 전략은 초기 위치에서 move_1과 move_2중 더 적은 횟수를 갖는 쪽으로 이동했다 돌아와서 택하지 않은 방향으로 이동하는 것이다. 따라서 move_1과 move_2 을 더하고, 둘 중 더 작은 쪽을 추가로 더한다.
뚤고가기
뚫고가기는 모든 위치를 순회하는 전부순회와 비슷하다. 그러나 A의 묶음이 우측에 존재한다면 그 묶음이 시작하기 직전에 멈출 수 있다.

이때, 돌아가기가 유리해 보이는 상황에서도 뚤고가기가 최적인 경우가 존재한다. 따라서 마지막으로 둘을 비교하여 더 작은 쪽을 이용한다.
code
def solution(name):
ASCII_A = ord("A")
right_As = 0 # 우측에 연이은 A의 개수
max_As = 0 # 최대 연이은 A의 개수
cur_As = 0
start_idx = None # 최대로 연속된 A가 시작하는 위치
last_idx = None # 최대로 연속된 A가 끝나는 위치
answer = 0
for idx, char in enumerate(name):
if char != "A":
cur_As = 0
difference = ord(char) - ASCII_A
if difference <= 13:
answer += difference
else:
answer += 26 - difference
continue
cur_As += 1
if cur_As > max_As:
max_As = cur_As
last_idx = idx + 1
start_idx = idx - max_As + 1
if idx == len(name) - 1 and char == "A":
while name[idx] == "A":
right_As += 1
idx -= 1
if start_idx is not None: # A가 존재할때
if right_As:
answer_straight = len(name) - 1 - right_As # 뚫고가기
if max_As > start_idx - 1 or max_As > len(name) - last_idx: # 돌아가기가 유리한 경우
move_1 = max(start_idx - 1, 0)
move_2 = len(name) - last_idx
answer_detour = min(move_1, move_2) + move_1 + move_2
answer += min(answer_straight, answer_detour) # 최적값을 선택한다
else: # 뚫고가기가 유리한 경우
answer += len(name) - 1 - right_As
else: # 전부 순회하는 경우
answer += len(name) - 1
return answer