
Sentencepiece tokenizer는 언어에 무관하고, 띄어쓰기 유무에 영향을 받지 않으며, 매우 빠르고, 기존의 vocab_size를 벗어난 경우 발생하던 [UNK] 토큰을 확연히 줄여줍니다. 어절 안쪽을 쪼개서("안녕하세요" -> "안녕, 하세요") tokenize하기 때문에 더 발전된 언어 모델을 만들 수 있습니다. 그 원리는 무엇일까요?
KAIST AAILab youtube 기계학습 강좌 1~9강, SentencePiece Demystified을 참고했습니다
Unigram Language Model
글은 순서를 갖는 sequence 이기 때문에 어떠한 문장이든 앞에 나온 단어에 기반하여 뒤에 나올 단어를 유추할 수 있습니다.
- ex) 오늘 마라탕 먹어야 하는데 같이 갈 사람 구함
위 문장에서 맥락을 고려한다면 "갈" 뒤에 "사람" 이 나올 확률은 "앵무새" 보다 높을 것입니다. 이전 몇 개의 토큰을 바탕으로 예측하는지에 따라 N-gram 에서 N이 바뀝니다. 이를 N-gram model이라고 합니다. 예를 들어, N=2인 경우 bigram model이 되며, 오늘 마라탕, 마라탕 먹어야 등에서 볼 수 있듯 직전 1개의 토큰을 고려한 확률분포를 사용합니다.
그러나 unigram model은 맥락을 전혀 신경쓰지 않습니다.어떠한 문장이 등장할 확률은 그저 전체 말뭉치(Corpus)에서 각 토큰이 등장할 확률을 곱한 것에 불과하고, 이는 토큰의 순서를 고려하지 않으므로 어절별로 토큰화한다고 했을 때
-
ex) 오늘 마라탕 먹어야 하는데 같이 갈 사람 구함
-
ex) 오늘 사람 갈 먹어야 하는데 마라탕 같이 구함
위의 두 문장은 같은 등장 확률을 보입니다.
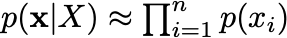
구현한 SentencePiece 역시 Unigram Model을 사용하고, 정식 package는 Byte Pair Encoding 혹은 Unigram(특정한 tokenizer model)을 지원합니다.
Byte Pair Encoding
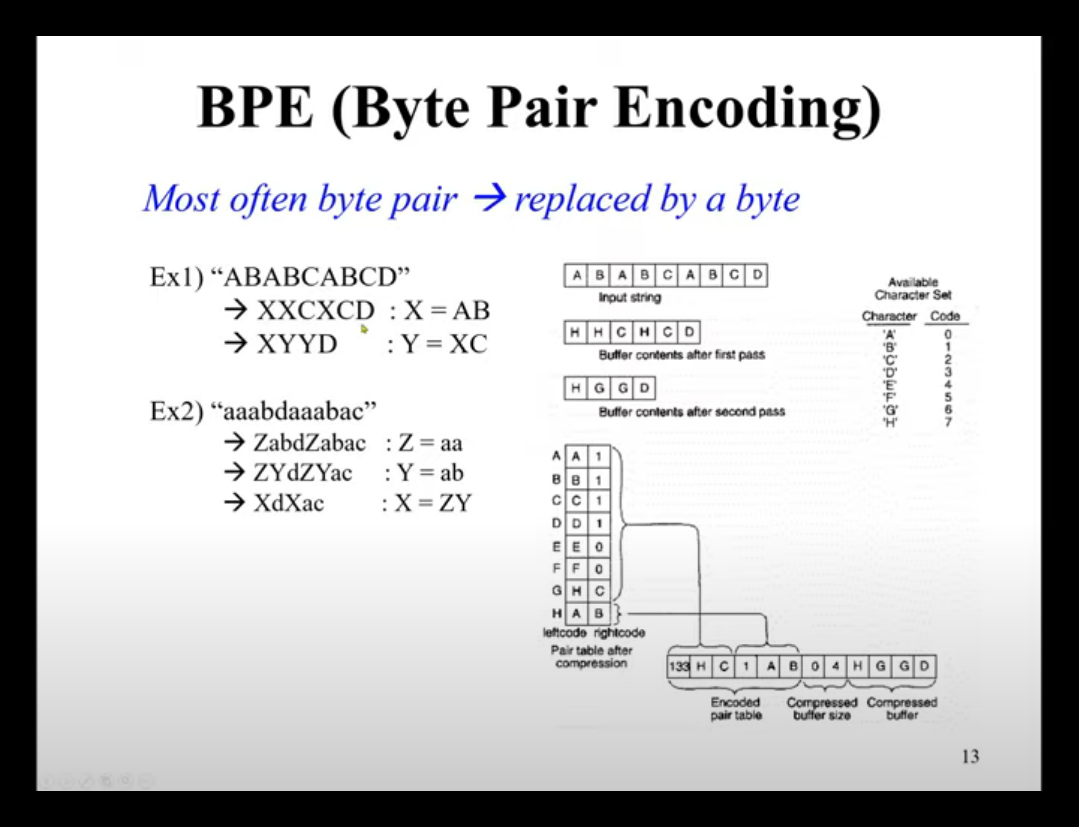
BPE는 말뭉치에서 자주 등장하는 연이은 토큰이 있다면, 그것을 하나의 토큰으로 합쳐버리는 과정입니다. 아래의 그림에서 AB가 X로 , XC가 Y로 바뀌는 과정이 핵심입니다. 이 때, 합쳐진 토큰의 등장 빈도도 함께 저장합니다. BPE는 SentencePiece 모델에서 초기 unigram 빈도를 얻는데 활용됩니다.
import re
import collections
class BytePairEncoder:
def __init__(self):
self.merges = None
self.characters = None
self.tokens = None
self.vocab = None
def format_word(self, text, space_token="_"):
return " ".join(list(text)) + " " + space_token
def initialize_vocab(self, text):
text = re.sub("\s+", " ", text)
all_words = text.split()
vocab = {}
for word in all_words:
word = self.format_word(word)
vocab[word] = vocab.get(word, 0) + 1
tokens = collections.Counter(text)
return vocab, tokens
def get_bigram_counts(self, vocab):
pairs = {}
for word, count in vocab.items():
symbols = word.split()
for i in range(len(symbols) - 1):
pair = (symbols[i], symbols[i + 1])
pairs[pair] = pairs.get(pair, 0) + count
return pairs
def merge_vocab(self, pair, vocab_in):
vocab_out = {}
bigram = re.escape(" ".join(pair))
p = re.compile(r"(?<!\S)" + bigram + r"(?!\S)")
bytepair = "".join(pair)
for word in vocab_in:
w_out = p.sub(bytepair, word)
vocab_out[w_out] = vocab_in[word]
return vocab_out, (bigram, bytepair)
def find_merges(self, vocab, tokens, num_merges):
merges = []
for i in range(num_merges):
pairs = self.get_bigram_counts(vocab)
best_pair = max(pairs, key=pairs.get)
best_count = pairs[best_pair]
vocab, (bigram, bytepair) = self.merge_vocab(best_pair, vocab)
merges.append((r"(?<!\S)" + bigram + r"(?!\S)", bytepair))
tokens[bytepair] = best_count
return vocab, tokens, merges
def fit(self, text, num_merges):
vocab, tokens = self.initialize_vocab(text)
self.characters = set(tokens.keys())
self.vocab, self.tokens, self.merges = self.find_merges(
vocab, tokens, num_merges
)
if __name__ == "__main__":
bpe = BytePairEncoder()
for i in range(0, 3):
bpe.fit("house home hostile", i)
print("--" * 12)
print(f"BPE vocabs - {i} merges")
print(bpe.vocab, "\n")
print(f"BPE tokens - {i} merges")
print(bpe.tokens)
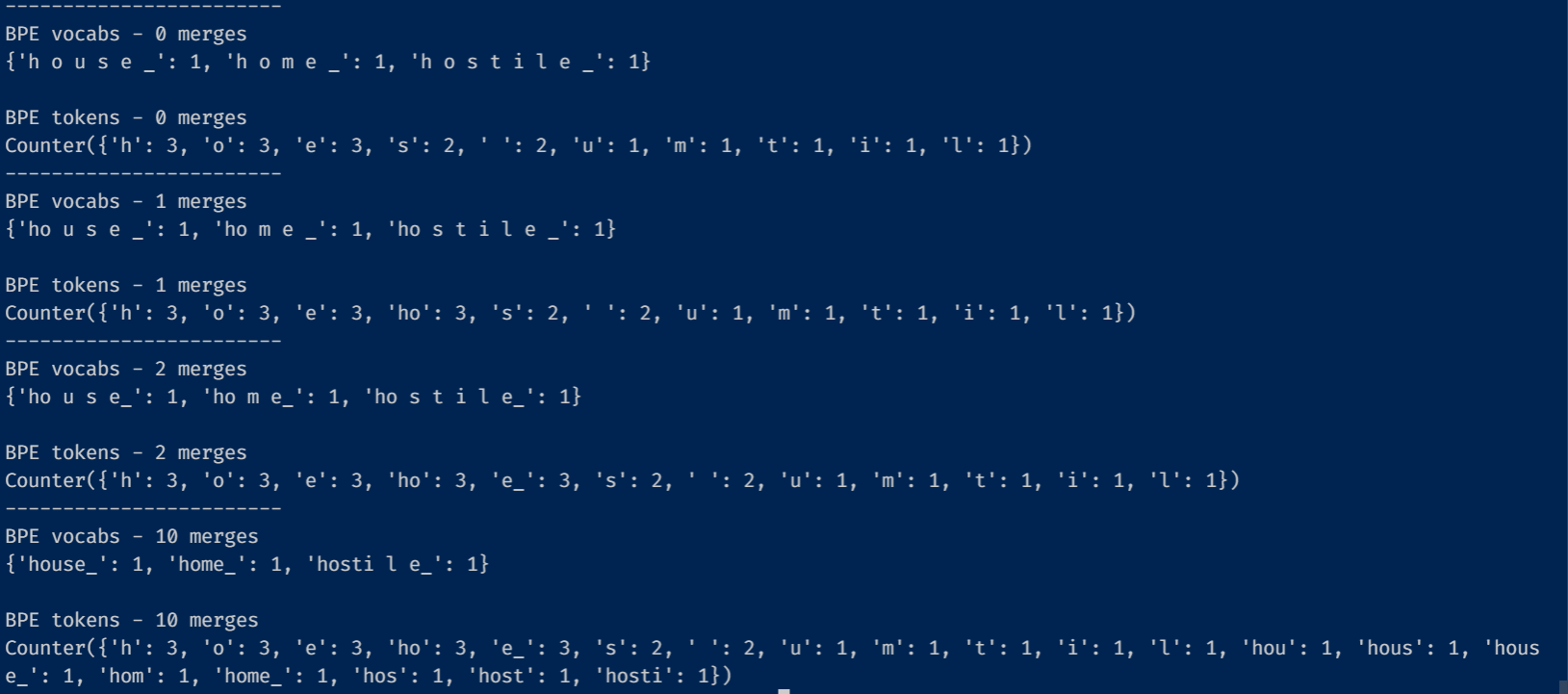
"house home hostile"로 BPE를 해본 결과입니다. 초기에는 'h o u s e _' 처럼 모든 글자가 분해되어 있고, 토큰 역시 한 글자씩 이루어진 것을 볼 수 있습니다. 1번 merge하면, 'ho u s e _', 'ho m e _'로 'ho'가 합쳐지고, 'ho'와 그 등장빈도 3번이 토큰에 기록되었습니다. 2번째 merge에서는 'e_'가 추가되었습니다.
Training SentencePiece
SentencePiece를 훈련하는 과정은 Variational inference의 일종으로, 관측한 데이터(Evidence)와 모델 파라미터(theta)가 있을 때, 가설(Hypothesis)에 대한 분포 를 variational parameter 를 도입해 로 근사합니다. 근사의 목적은 자체를 찾아내는 것은 너무 복잡하기 때문입니다. 이때 가 여러 개일 경우 각각은 서로 독립이고, 해당하는 숨겨진 변수에만 의존한다는 Mean Field theory를 사용합니다.
근사의 목적은 Evidence Lower Bound 를 극대화하는 것으로, 이 값이 커질수록 근사 와 실제의 사후분포 의 차이가 작아집니다.
동시에 최적화(의 극대화) 하는 대신, 각 마다 차례로 최적화한다면,
번째 variational parameter 에 대해 극대화해야 하는 식은 다음과 같습니다.
정리하면 아래의 식이 됩니다
KL Divergence는 0 이상이므로, 를 최대화하려면 KLD를 0으로 만들면 되고, 이는 두 분포를 같게 만듦으로서 실현됩니다. 따라서 아래와 같은 결론을 얻습니다
이 계산을 하다보면 의 분포를 계산할 때, 의 기댓값, 분산이 필요한 경우가 있습니다. 특히 서로의 기댓값 등을 필요로 하는 경우, 에 대해 최적화하고, 이를 바탕으로 에 대해 최적화하고, 다시 에 대해 최적화하여 분포가 수렴할 때까지 iterative하게 반복하는 coordinated optimization을 사용하는데, SentencePiece도 그런 경우입니다.
SentencePiece의 evidence log-likelihood
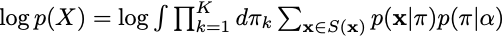
unigram probability를 사용하기 위해 숨겨진 변수 를 도입합니다. 또한 베이즈 정리를 사용하기 위해, 사전분포로 Dirichlet Distribution을 이용합니다. Dirichlet Distribution은 model parameter 에 의존하는 확률분포로 베이즈 정리에 의해 다음이 성립할 때,
다항분포를 가능도로, Dirichlet Distribution을 사전분포로 하는 경우 사후분포 역시 Dirichlet Distribution이 되어 conjugacy를 가지므로, 다항 분포의 모델링에 장점이 있어 Dirichlet prior을 사용합니다.
는 sequence에서 번째 토큰이 번째 unigram인 경우에는 1이고, 아닌 경우에는 0이 되어, 는 sequence을 특정한 segmentation으로 tokenize 했을 때, 등장하는 각 토큰의 unigram probability을 곱한 것과 같습니다. (unigram language model)
중간정리) 는 unigram probability를 표현하기 위해 도입한 숨겨진 변수(variational parameter)이며, 는 BPE 등으로 얻어진 가능한 토큰을 표현하기 위해 도입한 숨겨진 변수(variational parameter)입니다.(ex- h ell o 로 쪼개졌다면 h, ell, o 모두 로 표현할 수 있습니다 )
사후분포 를 추정하기 위해 mean field 근사로 두 변수이 독립이라고 하면, 위 섹션의 결론인 ()에 의해 다음이 성립합니다.
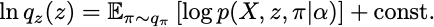
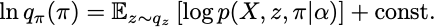
실제 분포를 넣어서 계산하면 다음으로 정리할 수 있습니다.
와 에 대해 기댓값을 구해보면,
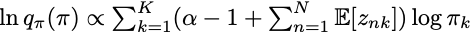
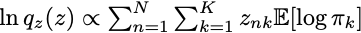
이 되므로 와 의 기댓값이 엮여 있어 coordinated optimization을 시행해야 합니다.
추가적인 정리를 하면 는 Dirichlet Distribution의 형태인 것을 알 수 있고, 는 등장 유무를 로 표현하는 변수이므로, 기댓값은 등장 횟수에 의존합니다. 번째 토큰에 대한 의 기댓값은 새로운 변수를 도입하여 다음과 같이 표현할 수 있습니다.
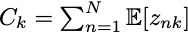
Dirichlet Distribution의 기댓값은 Digamma function 을 이용해 표현할 수 있으므로, (wikipedia)
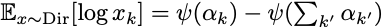
와 에서 기댓값을 위에서 얻은 수식을 통해 정리할 수 있습니다.
를 로 업데이트하여 계산합니다. 이때 는 model parameter가 로 변화한 것을 고려하여 coordinated optimization 한다면 다음과 같습니다.
마지막으로, 를 0으로 지정합니다.
와 에 대해 와 가 수렴할때까지 교대로 최적화한다면 는 원래의 분포의 좋은 근사가 됩니다.
python code에서는 가장 높은 확률을 갖는 tokenization을 구한 뒤, 토큰의 등장 빈도를 업데이트하는 과정의 반복으로 구현되었습니다.
자세한 python 코드 구현은 reference를 참고 바랍니다
Reference
SentencePiece Demystified: 코드 구현 및 설명의 일부를 이용했습니다.
Dirichlet Distribution: Conjugate Prior for Multinomial Distribution
