시간복잡도 + Big O를 이용한 점진적 접근

⏰ 1. 시간복잡도란?

알고리즘이 입력 크기(n)에 따라 얼마나 빠르게 실행되는지를 나타내는 척도입니다.

• 코드가 실행되는데 걸리는 시간을 측정하는 것이 아니라,

• 입력의 크기가 커졌을 때 얼마나 시간이 늘어나는지를 표현합니다.

✅ 예시: 두 코드의 차이

// 1번: 1부터 n까지 더하기 (반복문)
int sum = 0;
for (int i = 1; i <= n; i++) {
    sum += i;
}

→ 시간복잡도: O(n) ← n번 반복함

// 2번: 가우스 공식 이용
int sum = n * (n + 1) / 2;

→ 시간복잡도: O(1) ← 실행 시간은 입력 크기와 무관

🧠 2. 점근적 표기법 (Asymptotic Notation)

"입력 크기 n이 매우 커졌을 때" 알고리즘의 성능을 평가하는 방식

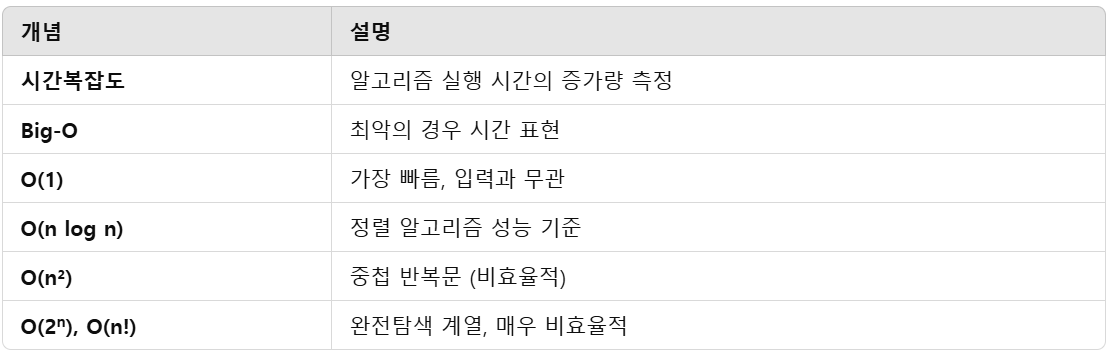
🔹 Big-O (O) – 최악의 경우

• 가장 많이 사용하는 표기

• 가장 느린 경우의 성능

🔹 Ω (오메가) – 최선의 경우

• 최소 시간 (가장 빨리 끝나는 경우)

🔹 Θ (세타) – 평균적인 경우

• 알고리즘의 정확한 성능 (상한 & 하한이 같을 때)

✅ 실무에서는 주로 Big-O를 사용합니다 (최악의 경우를 대비하기 위해)

📏 3. Big-O 시간복잡도 표

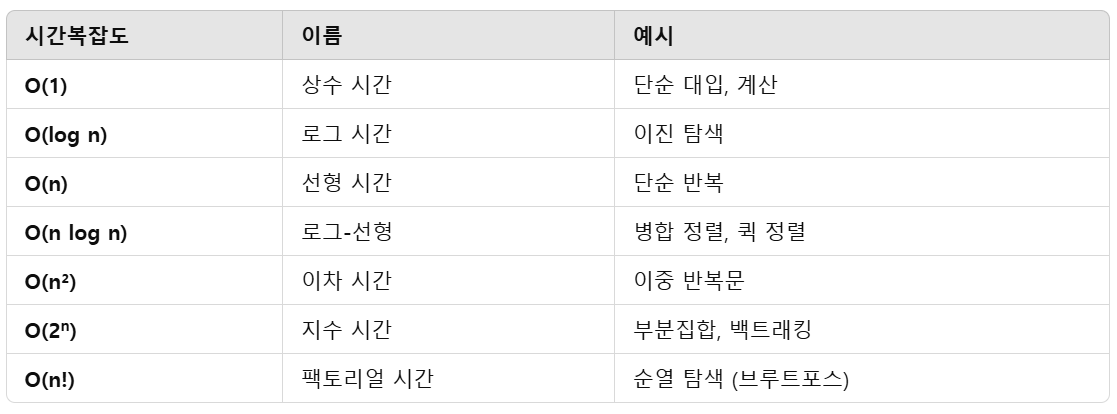
✅ 예제 코드별 시간복잡도

1️⃣ O(1)

int a = arr[0]; // 인덱스 접근은 상수 시간

2️⃣ O(n)

for (int i = 0; i < n; i++) {
    System.out.println(arr[i]);
}

3️⃣ O(n²)

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        System.out.println(i + ", " + j);
    }
}

4️⃣ O(log n)

// 이진 탐색
int binarySearch(int[] arr, int target) {
    int left = 0, right = arr.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (arr[mid] == target) return mid;
        else if (arr[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

📚 보충 개념: 시간복잡도 계산법

• 반복문 한 번 → O(n)

• 이중 반복문 → O(n²)

• 반으로 나누는 반복문 → O(log n)

• 재귀 함수 호출이 분기되는 경우 → O(2ⁿ), O(n!) 가능

💡 공간복잡도(Space Complexity)도 있어요

알고리즘이 사용하는 메모리의 양을 측정하는 개념

예: 배열을 n개 만든다면 → O(n) 공간복잡도

🎯 정리 요약