1. 정수론

소수(Prime Number)

정의: 1과 자신 이외의 양의 정수로 나누어 떨어지지 않는 수
응용: 소수 판별, 소수 나열, 소인수 분해, 최대공약수

Greatest Common Divisor(GCD)와 Greatest Common Divisor (LCM)

정의: 두 수의 가장 큰 공약수를 GCD, 가장 작은 공배수를 LCM이라고 함
응용: 유클리드 알고리즘으로 GCD 계산, LCM(a,b) = a*b/GCD(a,b) 관계로 LCM 계산

모듈러 연산 (Modular Arithmetic)

정의: 주어진 정수 n에 대해 나머지 값에만 관심을 갖는 연산
응용: 큰 수 연산의 오버플로 방지, 암호학, 고속 거듭제곱
(줄여서 mod)

확장된 유클리드 알고리즘 (Extended Euclidean Algorithm)

Euclidean algorithm

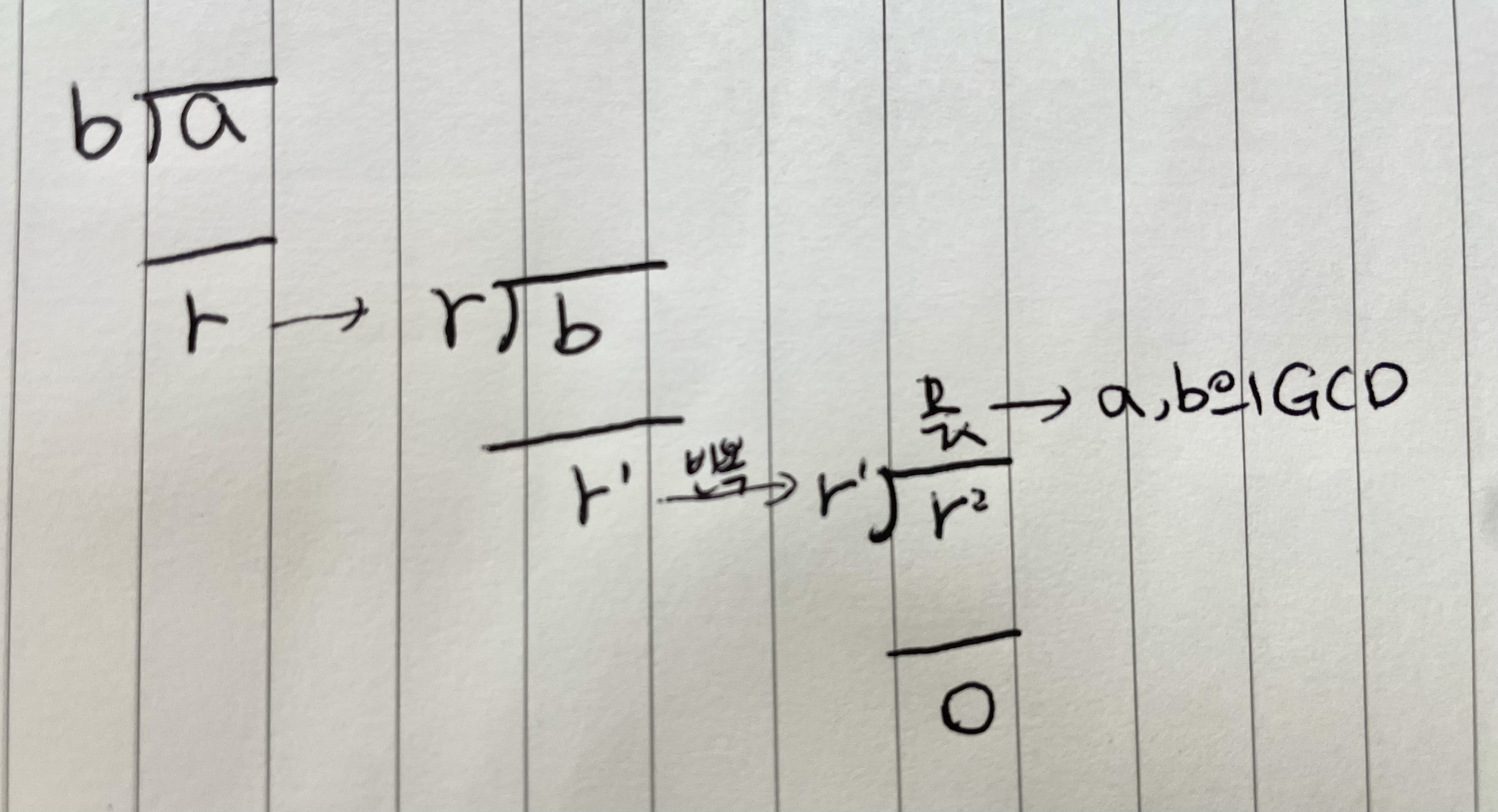
정의: GCD 계산을 확장하여 ax + by = GCD(a, b) 형태의 해 (x, y) 찾기
응용: 모듈러 역원 계산, 선형 디오판틴 방정식의 해

페르마의 소정리 (Fermat's Little Theorem)

정의: p가 소수이고 a가 p의 배수가 아닐 때, a^(p-1) ≡ 1 mod p 성립
응용: 모듈러 연산의 거듭제곱 계산, 소수 판별 (페르마 테스트)

중국인의 나머지 정리 (Chinese Remainder Theorem)

정의: 서로소인 모듈러 값들에 대한 연립 나머지 방정식의 해 찾기
응용: 큰 수 연산, 동시 합동 시스템

2. 탐색

분할정복

재귀에서 쓰는 방법. 큰 문제를 작은 문제들로 쪼개서

완전탐색

brute force attack. 모든 방법을 시도

이분탐색

퀵소트랑 비슷. 트리구조. 탐색 범위를 줄여가면서. 업앤다운 게임. 정렬 되있을때만 쓸 수 있겠다.
그럼 퀵소트 같은 경우에는 이분탐색 plus 분할정복 이겠다.

깊이 우선 탐색

3. 문제풀이

백트랙킹

정의: 해를 찾는 도중 해가 아니어서 막히면, 되돌아가서 다시 해를 찾아가는 기법
응용: 임의의 집합(set)에서 주어진 기준(criterion)대로 원소의 순서를 선택하는 문제를 푸는데에 적합(N-Queen,부분집합의 합, 0-1 배낭문제, etc)

• 트리 자료구조의 변형된 깊이우선탐색
• 모든 사례에 대해 효율적이라고 할 수는 없지만 많은 문제사례에 대해서 효율적.

미로찾기 문제를 생각하면 막다른 길을 만났을 때 스택을 이용해서 해결할 수 있었다.
이 문제를 트리 탐색 문제로 해석하면

• 갈림길을 하나의 노드(갈래 길의 왼쪽은 왼쪽 서브트리, 오른쪽은 오른쪽 서브트리)
• 깊이우선탐색(DFS)를 통한 문제 해결. 트리 구조의 preorder 방문

백트랙킹에는 상태공간트리(State Space Tree)가 있어야한다.

• 상태공간 : 해답을 탐색하기 위한 탐색 공간
• 상태공간트리 : 탐색 공간을 트리 형태의 구조로 암묵적으로 해석. 트리를 구현할 필요 없이 배열이 있다고 해도 트리로 해석하는 것.

최적화 문제라면 모든 상태공간 트리를 DFS로 방문해야 한다.

유망함(promising) : 하위 노드가 해답을 발견할 가능성이 있으면 promising. 아니면 nonpromising.

가지치기(pruning) : 방문중인 노드가 유망한지 체크. 유망하지 않으면 부모 노드로 되돌아감.(백트랙킹)

• 유망하지 않으면 하위 트리를 가지치기함
• 가지치기한 상태(pruned state): 방문한 노드의 방문하지 않은 하위 트리

일반적인 백트랙킹 알고리즘

def checknode (node v):
node u
if promising(v):
   if (v에 해답이 있으면)
       해답을 출력;
   else
       for (v의 모든 자식 노드 u에 대해서)
         checknode(u)