1026-TIL(DP, Greedy, Pointer)

동적 프로그래밍

1. DP는 큰 문제를 작은 문제들로 분할하여 그것을 이용해 큰 문제를 해결하는 방법입니다.

2. 분할정복과 다른점은 DP의 경우 작은 부분 문제의 답이 항상 같아야 한다는것 입니다.

problem과 subproblem을 정의하는게 어렵다. 문제에 많이 노출되는 수 밖에 없다.

그리디 알고리즘

1. 기본 개념 이해

• 그리디 알고리즘이란?

  그리디 알고리즘(그리디 알고리즘, Greedy Algorithm)은 문제를 해결할 때 항상 그 순간에 가장 최적인 선택을 하는 알고리즘 설계 방법입니다. 그리디 알고리즘은 각 단계에서 현재 상황에서 최선의 선택을 하는 방식으로 동작하며, 이 선택들의 조합이 전체 문제의 최적해가 되는 것을 기대합니다.

• 최적 부분 구조 & 탐욕적 선택 속성의 개념

  최적 부분 구조 (Optimal Substructure): 최적 부분 구조란 전체 문제를 부분 문제로 나눌 수 있고 각 부분 문제가 독립적으로 최적해를 가지는 성질을 의미합니다.

  탐욕적 선택 속성 (Greedy Choice Property): 그리디 알고리즘이 항상 최적해를 찾을 수 있는지 여부는 문제마다 다르며, 이를 판단하기 위해 탐욕적 선택 속성을 사용합니다. 탐욕적 선택 속성은 각 단계에서 한 번 선택한 요소를 다시 선택하지 않는 것이 좋은 선택일 때 적용됩니다.

• 그리디 알고리즘의 장단점

  장점	단점
  간단하고 직관적	최적해를 보장하지 않는 경우
  빠른 실행 시간	전체 문제 고려 부족
  메모리 사용량 낮음	문제 의존성
  일부 문제에 대해 최적해 보장	복잡한 문제 처리 어려움

2. 탐욕적 선택 기법과 동적 프로그래밍의 차이점

탐욕적 선택 기법은 각 단계에서 현재 최선의 선택을 하는 간단한 방법이며, 최적해를 보장하지 않는 경우가 많지만 빠르게 동작합니다. 반면, 동적 프로그래밍은 부분 문제의 최적해를 계산하고 이를 이용하여 전체 문제의 최적해를 찾는 더 복잡한 방법이며, 최적해를 보장하고 메모이제이션을 사용하여 중복 계산을 피합니다.

특성	탐욕적 선택 기법	동적 프로그래밍
기본 개념	현재 단계에서 가장 최선의 선택	부분 문제의 최적해를 계산하고 이를 이용하여 전체 문제의 최적해를 찾음
문제 유형	일부 문제에 적합	많은 종류의 문제에 적용 가능
최적해 보장 여부	보장되지 않는 경우가 많음	보장됨
부분 문제 간의 관계	독립적이며 중복이 없음	종종 중복되는 부분 문제가 있음
메모이제이션 (Memoization) 사용	사용하지 않음	사용함
시간 복잡성	일반적으로 빠름	부분 문제의 개수와 관련이 있음
공간 복잡성	메모리 사용량이 낮음	추가 메모리 사용
예시	거스름돈 문제, 프림 알고리즘	피보나치 수열 계산, 최단 경로 알고리즘

3. 그리디 알고리즘의 유형

• 활동 선택 문제
• 거스름돈 문제
• 허프만 코딩
• 프림 알고리즘
• 크루스칼 알고리즘

4. 탐욕적 선택 기법

• 동전 거스름돈 문제
• 프랙탈 러거
• 태스크 스케줄링
• 다익스트라 알고리즘

5. 실전 예제 및 응용

• 스케줄링과 태스크 배정 문제
• 최소 신장 트리 구축
• 문제 해결을 위한 그리디 알고리즘 적용

6. 그리디 알고리즘의 한계와 제약 사항

• 최적해가 보장되지 않는 경우

a. 최적 부분 구조 부재: 만약 문제가 최적 부분 구조를 가지지 않는다면, 그리디 알고리즘을 사용하는 것이 어려울 수 있습니다. 최적 부분 구조란 전체 문제를 부분 문제로 나눌 수 있고 각 부분 문제가 독립적으로 최적해를 가질 때 해당합니다.

b. 탐욕적 선택 속성이 부재: 탐욕적 선택 속성은 각 단계에서 한 번 선택한 요소를 다시 선택하지 않는 것이 좋은 선택일 때 적용됩니다. 만약 이 속성이 부재하면 그리디 알고리즘이 최적해를 보장하지 않을 수 있습니다.

c. 음수 가중치 혹은 비선형 문제: 그리디 알고리즘이 일부 문제에는 효과적이지만, 음수 가중치가 있는 경우나 비선형 문제 등에는 적합하지 않을 수 있습니다.

d. 완전 탐색 필요: 만약 문제가 모든 가능한 상태나 조합을 탐색해야 하는 경우, 그리디 알고리즘은 최적해를 보장하지 않을 수 있습니다. 이런 경우 동적 프로그래밍이나 백트래킹과 같은 전체 탐색 알고리즘을 고려해야 합니다.

e. 문제의 제약 조건: 문제의 제약 조건이 그리디 알고리즘을 사용하기 어렵게 만드는 경우도 있습니다. 예를 들어, 최단 경로 문제에서 음수 가중치 엣지가 있는 경우 그리디 알고리즘을 사용하기 어려울 수 있습니다.

f. 프렉탈 문제: 프렉탈 문제와 같이 자기 유사한 패턴이 반복되는 경우, 그리디 알고리즘이 최적해를 보장하지 않을 수 있습니다.

이러한 경우들을 고려할 때, 그리디 알고리즘을 사용하기 전에 문제의 특성과 제약을 신중하게 검토하고, 최적해가 보장되지 않을 가능성을 고려해야 합니다. 때로는 다른 알고리즘을 사용해야 하며, 알고리즘 선택에 대한 이해가 중요합니다.

• 예외 상황 및 한계

7. 그리디를 응용하는 알고리즘

• 거스름돈 문제 (Change-Making Problem): 가장 작은 동전 개수로 거스름돈을 주는 문제로, 그리디 알고리즘을 사용하여 해결할 수 있습니다.

• 최소 신장 트리 (Minimum Spanning Tree): 프림 알고리즘과 크루스칼 알고리즘은 그리디 알고리즘을 사용하여 최소 신장 트리를 찾는데 활용됩니다.

• 최단 경로 문제 (Shortest Path Problem): 다익스트라 알고리즘과 벨만-포드 알고리즘은 그리디 알고리즘을 사용하여 최단 경로를 찾는 문제를 해결하는 데 사용됩니다.

• 캐시 알고리즘 (Cache Algorithms): LRU (Least Recently Used)와 LFU (Least Frequently Used)와 같은 캐시 알고리즘은 그리디 방식을 사용하여 캐시의 데이터 교체 정책을 결정합니다.

• 허프만 코딩 (Huffman Coding): 데이터 압축 알고리즘 중 하나로, 그리디 알고리즘을 사용하여 각 문자의 이진 코드를 생성합니다.

• 작업 스케줄링 (Job Scheduling): 작업을 처리하는데 걸리는 시간과 데드라인이 주어진 경우, 그리디 알고리즘을 사용하여 작업 스케줄링을 수행할 수 있습니다.

• 부분 배낭 문제 (Fractional Knapsack Problem): 제한된 가방 용량 내에서 물건을 최대한 가치 있게 넣는 문제를 그리디 알고리즘으로 풀 수 있습니다.

• 스케줄링 문제 (Scheduling Problem): 각 작업의 시작 및 종료 시간이 주어진 경우, 그리디 알고리즘을 사용하여 작업을 최적으로 스케줄링할 수 있습니다.

• 클러스터링 (Clustering): 데이터를 그룹화하는 문제에서 그리디 알고리즘을 사용하여 데이터 포인트를 클러스터로 그룹화합니다.

• 최소 비용 신경망 문제 (Minimum Cost Spanning Tree Problem): 그리디 알고리즘을 사용하여 최소 비용 신경망을 생성하는데 활용됩니다.

8. 실제 응용 분야

• 그리디 알고리즘의 실제 응용 사례: 스케줄링, 압축 알고리즘, 네트워크 라우팅 등

그리디 알고리즘의 정당성

그리디 알고리즘으로 해법을 찾았을 때에는 그 해법이 정당한지 검토 할 수 있어야 답을 도출할 수 있다.

포인터

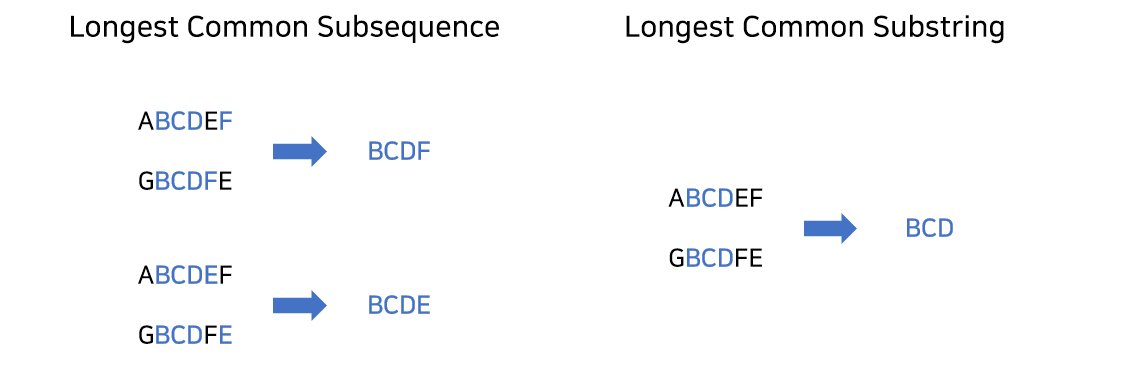
LCS