left_rotation 부터 format 다시 맞추기
rbtree
following the psuedo
new_rbtree(void)
이건 psudo code가 교재에 없다
static node_t *new_node(const key_t key, node_t *nil) {
node_t *newNode = (node_t *)malloc(sizeof(node_t));
newNode->parent = nil;
newNode->left = nil;
newNode->right = nil;
newNode->key = key;
newNode->color = RBTREE_RED;
return newNode;
}
rbtree *new_rbtree(void) {
rbtree *t = (rbtree *)calloc(1, sizeof(rbtree));
t->nil = (node_t *)malloc(sizeof(node_t));
t->nil->color = RBTREE_BLACK;
t->root = NULL;
return t;
}
Left/Right rotation
psuedo code
LEFT-ROTATE(T, x)
1 y = x.right
2 x.right = y.left
3 if y.left != T.nil
4 y.left.p = x
5 y.p = x.p
6 if x.p == T.nil
7 T.root = y
8 elseif x == x.p.left
9 x.p.left = y
10 else x.p.right = y
11 y.left = x
12 x.p = y수도코드 c언어로 옮기기
static void left_rotation(rbtree *t, node_t *x){
node_t *y = x->right; // y 설정
x->right = y->left; // y의 왼쪽 서브트리를 x의 오른쪽 서브트리로 옮긴다.
if (y->left != t->nil){
y->left->parent = x;
}
y->parent = x->parent; // x의 부모를 y로 연결한다.
if (x->parent == t->nil){
t->root == y;
} else if(x == x->parent->left){
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x; // x를 y의 왼쪽으로 놓는다.
x->parent = y;
}
static void right_rotation(rbtree *t, node_t *y){
node_t *x = y->left;
y->left = x->right;
if (x->right != t->nil) {
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == t->nil) {
t->root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}
x->right = y;
y->parent = x;
}Insertion
psuedo code
RB-INSERT(T, z)
1 y = T.nil
2 x = T.root
3 while x != T.nil
4 y = x
5 if z.key < x.key
6 x = x.left
7 else x = x.right
8 z.p = y
9 if y == T.nil
10 T.root = z
11 elseif z.key < y.key
12 y.left = z
13 else y.right = z
14 z.left = T.nil
15 z.right = T.nil
16 z.color = RED
17 RB-INSERT-FIXUP(T, z)수도코드 c언어로 옮기기
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *z = new_node(key, t->nil);
node_t *y = t->nil;
node_t *x = t->root;
while (x != t->nil){
y = x;
if (z->key < x->key){
x = x->left;
} else {
x = x->right;
}
}
z->parent = y;
if (y == t->nil){
t->root = z;
} else if (z->key < y->key){
y->left = z;
} else {
y->right = z;
}
z->left = t->nil;
z->right = t->nil;
z->color = RBTREE_RED;
rbtree_insert_fixup(t, z);
return z;
}Insert fixup
psuedo code
RB-INSERT-FIXUP(T, z)
1 while z.p.color == RED
2 if z.p == z.p.p.left
3 y = z.p.p.right
4 if y.color == RED
5 z.p.color = BLACK // case 1
6 y.color = BLACK // case 1
7 z.p.p.color = RED // case 1
8 z = z.p.p // case 1
9 else if z == z.p.right
10 z = z.p // case 2
11 LEFT-ROTATE(T, z)/ // case 2
12 z.p.color = BLACK // case 3
13 z.p.p.color = RED // case 3
14 RIGHT-ROTATE(T, z.p.p) // case 3
15 else (same for z.p as a z.p.p.right subtree) // case 4 ~ 6
16 T.root.color = BLACK
c로 옮기기
static void rbtree_insert_fixup(rbtree *t, node_t *z){
while (z->parent->color == RBTREE_RED){
if (z->parent == z->parent->parent->left){
node_t *y = z->parent->parent->right;
if (y->color == RBTREE_RED){
z->parent->color = RBTREE_BLACK; // case 1
y->color = RBTREE_BLACK; // case 1
z->parent->parent->color = RBTREE_RED; // case 1
z = z->parent->parent; // case 1
} else {
if (z == z->parent->right){
z = z->parent; // case 2
left_rotation(t,z); // case 2
}
z->parent->color = RBTREE_BLACK; // case 3
z->parent->color = RBTREE_RED; // case 3
right_rotation(t,z->parent->parent); // case 3
}
} else { // z->parent == z->parent->parent->right -> case 4~6 (위 while 밑 if 안에를 right를 left로 바꾼것과 같다)
node_t *y = z->parent->parent->left;
if (y->color == RBTREE_RED){
z->parent->color = RBTREE_BLACK; // case 1
y->color = RBTREE_BLACK; // case 1
z->parent->parent->color = RBTREE_RED; // case 1
z = z->parent->parent; // case 1
} else {
if (z == z->parent->left){
z = z->parent; // case 2
right_rotation(t,z); // case 2
}
z->parent->color = RBTREE_BLACK; // case 3
z->parent->color = RBTREE_RED; // case 3
left_rotation(t,z->parent->parent); // case 3
}
}
t->root->color = RBTREE_BLACK;
}
}버리기
gpt 참고용
#include "rbtree.h"
#include <stdlib.h>
#include <stdio.h>
// 주어진 키와 기본 속성으로 새 노드를 생성하는 도우미 함수
static node_t *new_node(const key_t key, node_t *nil) {
node_t *newNode = (node_t *)malloc(sizeof(node_t));
newNode->key = key;
newNode->left = nil;
newNode->right = nil;
newNode->parent = nil;
newNode->color = RBTREE_RED;
return newNode;
}
// 왼쪽 회전을 수행하는 도우미 함수
static void left_rotate(rbtree *t, node_t *x) {
node_t *y = x->right;
x->right = y->left;
if (y->left != t->nil) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == t->nil) {
t->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
// 오른쪽 회전을 수행하는 도우미 함수
static void right_rotate(rbtree *t, node_t *y) {
node_t *x = y->left;
y->left = x->right;
if (x->right != t->nil) {
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == t->nil) {
t->root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}
x->right = y;
y->parent = x;
}
// Red-Black 트리에서 위반 사항을 수정하는 도우미 함수
static void rbtree_insert_fixup(rbtree *t, node_t *z) {
while (z->parent->color == RBTREE_RED) {
if (z->parent == z->parent->parent->left) {
node_t *y = z->parent->parent->right;
if (y->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
} else {
if (z == z->parent->right) {
z = z->parent;
left_rotate(t, z);
}
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
right_rotate(t, z->parent->parent);
}
} else {
node_t *y = z->parent->parent->left;
if (y->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
} else {
if (z == z->parent->left) {
z = z->parent;
right_rotate(t, z);
}
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
left_rotate(t, z->parent->parent);
}
}
}
t->root->color = RBTREE_BLACK;
}
// 새로운 Red-Black 트리를 생성하고 그에 대한 포인터를 반환합니다
rbtree *new_rbtree(void) {
rbtree *t = (rbtree *)malloc(sizeof(rbtree));
t->nil = (node_t *)malloc(sizeof(node_t));
t->nil->color = RBTREE_BLACK;
t->root = t->nil;
return t;
}
// 트리의 모든 노드를 재귀적으로 삭제합니다
static void rbtree_delete_nodes(rbtree *t, node_t *node) {
if (node != t->nil) {
rbtree_delete_nodes(t, node->left);
rbtree_delete_nodes(t, node->right);
free(node);
}
}
// Red-Black 트리를 삭제하고 해당 메모리를 해제합니다
void delete_rbtree(rbtree *t) {
rbtree_delete_nodes(t, t->root);
free(t->nil);
free(t);
}
// 주어진 키를 가진 새로운 노드를 Red-Black 트리에 삽입합니다
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *z = new_node(key, t->nil);
node_t *y = t->nil;
node_t *x = t->root;
while (x != t->nil) {
y = x;
if (z->key < x->key) {
x = x->left;
} else {
x = x->right;
}
}
z->parent = y;
if (y == t->nil) {
t->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
rbtree_insert_fixup(t, z);
return z;
}
// 주어진 키와 일치하는 노드를 트리에서 찾는 도우미 함수
static node_t *rbtree_find_node(const rbtree *t, const key_t key) {
node_t *x = t->root;
while (x != t->nil) {
if (key == x->key) {
return x;
} else if (key < x->key) {
x = x->left;
} else {
x = x->right;
}
}
return t->nil;
}
// Red-Black 트리에서 주어진 키를 가진 노드를 찾습니다
node_t *rbtree_find(const rbtree *t, const key_t key) {
return rbtree_find_node(t, key);
}
// Red-Black 트리에서 최소 키를 가진 노드를 찾습니다
node_t *rbtree_min(const rbtree *t) {
node_t *x = t->root;
while (x->
응 망친거
#include "rbtree.h"
#include <stdlib.h>
#include <stdio.h>
// 새 노드 생성
static node_t *new_node(const key_t key, node_t *nil) {
node_t *newNode = (node_t *)malloc(sizeof(node_t));
newNode->key = key;
newNode->left = nil;
newNode->right = nil;
newNode->parent = nil;
newNode->color = RBTREE_RED;
return newNode;
}
// 트리 생성
rbtree *new_rbtree(void) {
// tree 구조체 생성
rbtree *t = (rbtree *)calloc(1, sizeof(rbtree));
// root 노드를 nil로 초기화
t->root = t->nil;
// nil_node 구조체 생성 및 초기화
node_t *nil_node = (node_t *)calloc(1, sizeof(node_t));
nil_node->color = RBTREE_BLACK; // nil node의 색깔은 블랙
// tree의 nil을 nil_node로 설정(tree가 빈 경우 root는 nil_node를 가리킴)
t->nil = nil_node;
return t;
}
// 각 노드와 그 자식 노드들의 메모리 반환 함수
void travle_and_delete_node(rbtree *t, node_t *node) {
if (node->left != t->nil) { // 왼쪽 자식이 nil 노드가 아닐 때까지
travle_and_delete_node(t, node->left);
}
if (node->right != t->nil) { // 오른쪽 자식이 nil 노드가 아닐 때까지
travle_and_delete_node(t, node->right);
}
free(node); // 노드 구조체 메모리 반환
}
// 트리 순회하며 각 노드의 메모리 반환
void delete_rbtree(rbtree *t) {
node_t *node = t->root;
if (node != t->nil) { // nil 노드가 아닐 때까지
travle_and_delete_node(t, node);
// 닐노드와 rbtree 구조체 메모리 반환
free(t->nil);
free(t);
}
}
// 왼쪽 회전 함수
void left_rotate(rbtree *t, node_t *node){
node_t *parent=node->parent;
node_t *grand_parent=parent->parent;
node_t *left_child=node->left;
// 부모가 루트인 경우: 현재 노드를 루트로 설정(노드를 삭제한 경우에만 발생)
if(parent==t->root){
t->root=node;
}
else{ // 부모가 루트가 아닌 경우: 조부모의 자식을 현재 노드로 설정
if(grand_parent->left==parent){ // 부모가 조부모의 왼쪽 자식인 경우
grand_parent->left=node;
}
else{ // 부모가 조부모의 오른쪽 자식인 경우
grand_parent->right=node;
}
}
node->parent=grand_parent; // 현재 노드의 부모를 조부모로 설정
parent->parent=node; // 조부모를 현재 노드로 설정
node->left=parent; // 현재 노드의 왼쪽 자식을 부모로 설정
parent->right=left_child; // 부모의 오른쪽 자식을 왼쪽 자식으로 설정
left_child->parent=parent; // 왼쪽 자식의 부모를 부모로 설정
}
// 오른쪽 회전 함수
void right_rotate(rbtree *t, node_t *node){
node_t *parent=node->parent;
node_t *grand_parent=parent->parent;
node_t *right_child=node->right;
// 부모가 루트인 경우: 현재 노드를 루트로 설정(노드를 삭제한 경우에만 발생)
if(parent==t->root){
t->root=node;
}
else{
if(grand_parent->left==parent){ // 부모가 조부모의 왼쪽 자식인 경우
grand_parent->left=node; // 1-1) 노드를 조부모의 왼쪽 자식으로 설정
}
else{ // 부모가 조부모의 오른쪽 자식인 경우
grand_parent->right=node;
}
}
node->parent=grand_parent; // 1-2) 현재 노드의 부모를 조부모로 설정
parent->parent=node; // 2-1) 조부모를 현재 노드로 설정
node->right=parent; // 2-2) 부모를 현재 노드의 오른쪽 자식으로 설정
right_child->parent=parent; // 3-1) 부모를 오른쪽 자식의 부모로 설정
parent->left=right_child; // 3-2) 오른쪽 자식을 부모의 왼쪽 자식으로 설정
}
void exchange_color(node_t *a, node_t *b)
{
int tmp = a->color;
a->color = b->color;
b->color = (tmp == RBTREE_BLACK) ? RBTREE_BLACK : RBTREE_RED;
}
// 불균형 해소 함수
void rbtree_insert_fixup(rbtree *t, node_t *node){
node_t *parent = node->parent; // 새 노드의 부모 노드
node_t *grandparent = parent->parent; // 새 노드의 조부모 노드
node_t *uncle; // 새 노드의 삼촌 노드
int is_left=node == parent->left; // 새 노드가 부모 노드의 왼쪽 자식인지 여부 (?여기 문법)
int is_parent_left_child; // 부모 노드가 조부모 노드의 왼쪽 자식인지 여부
// case0-1) 새 노드가 root인 경우: 새 노드를 black으로 변경
if(node==t->root){
node->color=RBTREE_BLACK;
return;
}
// case0-2) 새 노드의 부모 노드가 black인 경우: do nothing
if(parent->color==RBTREE_BLACK){
return;
}
is_parent_left_child=grandparent->left==parent; // 부모 노드가 조부모 노드의 왼쪽 자식인지 여부
uncle=is_parent_left_child?grandparent->right:grandparent->left; // 삼촌 노드 설정
// 부모가 레드인 경우 이제 약간 머리아픔(아래 3가지 케이스로 나뉨)
// case1) 부모와 삼촌 노드 모두가 red인 경우
// 부모와 삼촌 노드를 black으로 변경
// 조부모 노드를 red로 변경
// 조부모 노드의 불균형이 해소될 때까지 재귀적으로 불균형 해소
if(uncle->color==RBTREE_RED){
parent->color=RBTREE_BLACK;
uncle->color=RBTREE_BLACK;
grandparent->color=RBTREE_RED;
rbtree_inert_fixup(t,grandparent);
return;
}
// case 2 & 3 : 부모의 형제가 블랙
// case 2:
// case 2-1
// 부모가 왼쪽자식 & 내가 왼쪽 자식
// case 2-2
// 부모가 오른쪽자식 & 내가 오른쪽 자식
// case 3:
// case 3-1
// 부모가 왼쪽자식 & 내가 오른쪽
// case 3-2
// 부모가 오른쪽자식 & 내가 왼쪽
// 그래서 분기를 나누면 순서가 약간 뒤죽박죽인 느낌
// 부모가 왼쪽 자식일 때
// case2-1(내가 왼쪽) & 3-1(내가 오른쪽)
// 부모가 오른쪽 자식일 때
// case2-2(내가 오른쪽) & 3-2(내가 왼쪽)
// 이렇게 됨
if(is_parent_left_child){ // 부모가 왼쪽 자식일 때
if(is_left){ // case 2-1
right_rotate(t,parent);
exchange_color(parent,parent->right); //여기 말 됨?
}
else{ // case 3-1
left_rotate(t,node);
right_rotate(t,node);
exchange_color(node,node->right);
return;
}
} else { // 부모가 오른쪽 자식일 때 (나 근데 여기 궁금해 만약에 else안넣고 그냥 if(is_left)하면 안되낭)
if(is_left){ // case 3-2
right_rotate(t,node);
left_rotate(t,node);
exchange_color(node,node->left);
return;
}
else{ // case 2-2
left_rotate(t,parent);
exchange_color(parent,parent->left);
}
}
}
// insert 함수
node_t *rbtree_insert(rbtree *t, const key_t key) {
// 1) 새 노드 생성
node_t *new_node = (node_t *)calloc(1, sizeof(node_t));
new_node->key = key; // 새 노드의 key값 설정
new_node->color = RBTREE_RED; // 새 노드의 색깔은 레드
new_node->left = new_node->right = t->nil; // 새 노드의 자식 노드는 nil 노드를 가리킴
// 2) 새 노드를 삽입할 위치 탐색
node_t *current= t->root; // 현재 노드를 root 노드로 설정
while(current!=t->nil){ //
if (key < current->key) { // 새 노드의 key값이 현재 노드의 key값보다 작으면
if (current->left == t->nil) { // 현재 노드의 왼쪽 자식이 nil 노드이면
current->left = new_node; // 현재 노드의 왼쪽 자식으로 새 노드를 삽입
break;
}
current = current->left; // 현재 노드를 왼쪽 자식 노드로 설정
} else { // 새 노드의 key값이 현재 노드의 key값보다 크면
if (current->right == t->nil) { // 현재 노드의 오른쪽 자식이 nil 노드이면
current->right = new_node; // 현재 노드의 오른쪽 자식으로 새 노드를 삽입
break;
}
current = current->right; // 현재 노드를 오른쪽 자식 노드로 설정
}
}
new_node->parent = current; // 3) 새 노드의 부모 지정
if(current==t->root){ //root가 nil이면 새노드를 root로 지정
t->root=new_node;
}
// 불균형 발생 시 불균형 해소
rbtree_insert_fixup(t, new_node);
return new_node;
}
node_t *rbtree_find(const rbtree *t, const key_t key) {
// TODO: implement find
return t->root;
}
node_t *rbtree_min(const rbtree *t) {
// TODO: implement find
return t->root;
}
node_t *rbtree_max(const rbtree *t) {
// TODO: implement find
return t->root;
}
int rbtree_erase(rbtree *t, node_t *p) {
// TODO: implement erase
return 0;
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
// TODO: implement to_array
return 0;
}
csapp 7장 linker
7.1 Compiler Drivers
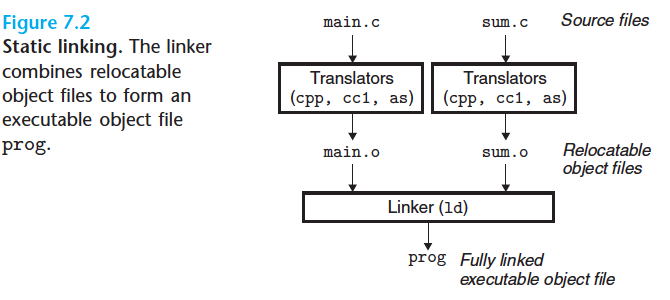
Drivers and the flow
-
C preprocessor(cpp) translates
C source filemain.c-> ASCII intermediate filemain.i -
C compiler(cc1) translates
main.i-> ASCII assembly-language filemain.s -
assembler(as) translates
main.s-> binary relocatable object filemain.o -
runs same process to generate sum.o
-
linker program(ld) combines
main.o+sum.o-> executable object fileprog
7.4 Relocatable Object Files
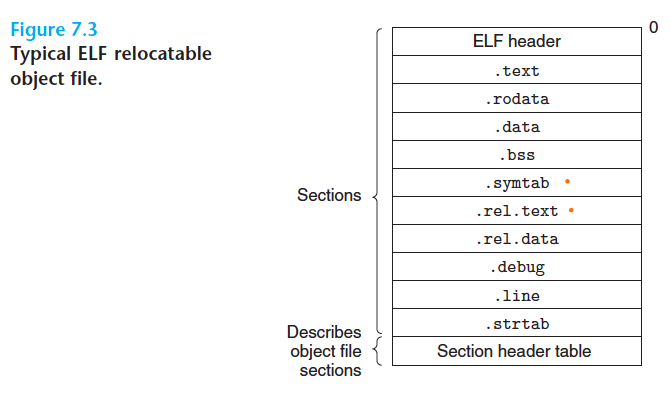
- .text - the machine code
- .rodata - Read-only data (such as format string in printf and jump tables for switch)
- .data - Initialized global and static C variables.
- .bss - (better save space) Uninitialized global and static C variables. 실제로 공간 차지 안함.
- .symtab - A symbol table with info about functions and global variables. 하지만 컴파일러 안에 있는 심볼테이블과 다르게 여기에선 local varibales를 위한 entries를 포함하지 않는다.
- .rel.text - A list of locations in the .text section that will need to be modified when the linker combines. 당연한 얘기지만 대부분의 외부 함수와 글로벌 변수는 수정이 필요하다. 반면 로컬은 수정될 필요가 없다.
- .debug - A devugging symbol table
- .line - A mapping btw line nums in the original C source program and machine code instructions in the
.text. - .strtab - A string table for the symbol tables in the
.symtaband.debugsection. 이 string table은 sequence of null-terminated character strings임.
7.9 Loading Executable Object Files
Loader 라는 친구는 아래와 같은 두가지 일을 한다.
- copies the code and data in the executable object file from disk into memory
- runs the program by jumping to its first instruction, or entry point
그래서 loading 이라고 말하는 것은 프로그램을 메모리에 카피하고 실행시키는 것을 일컫는다.
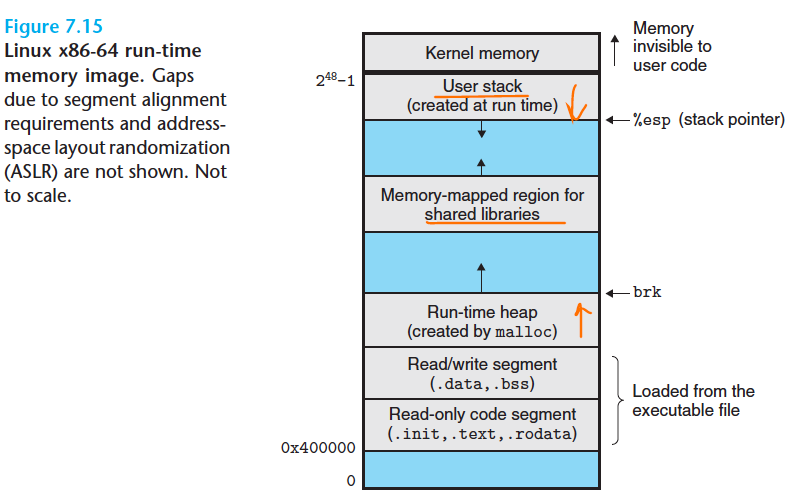
위 그림을 보면 Run-time heap이 아래에서 위로 자라고,
중간에 shared libs가 있고
User stack이 위에서 아래로 (낮은 주소 숫자로) 자라는 것을 볼 수 있다.
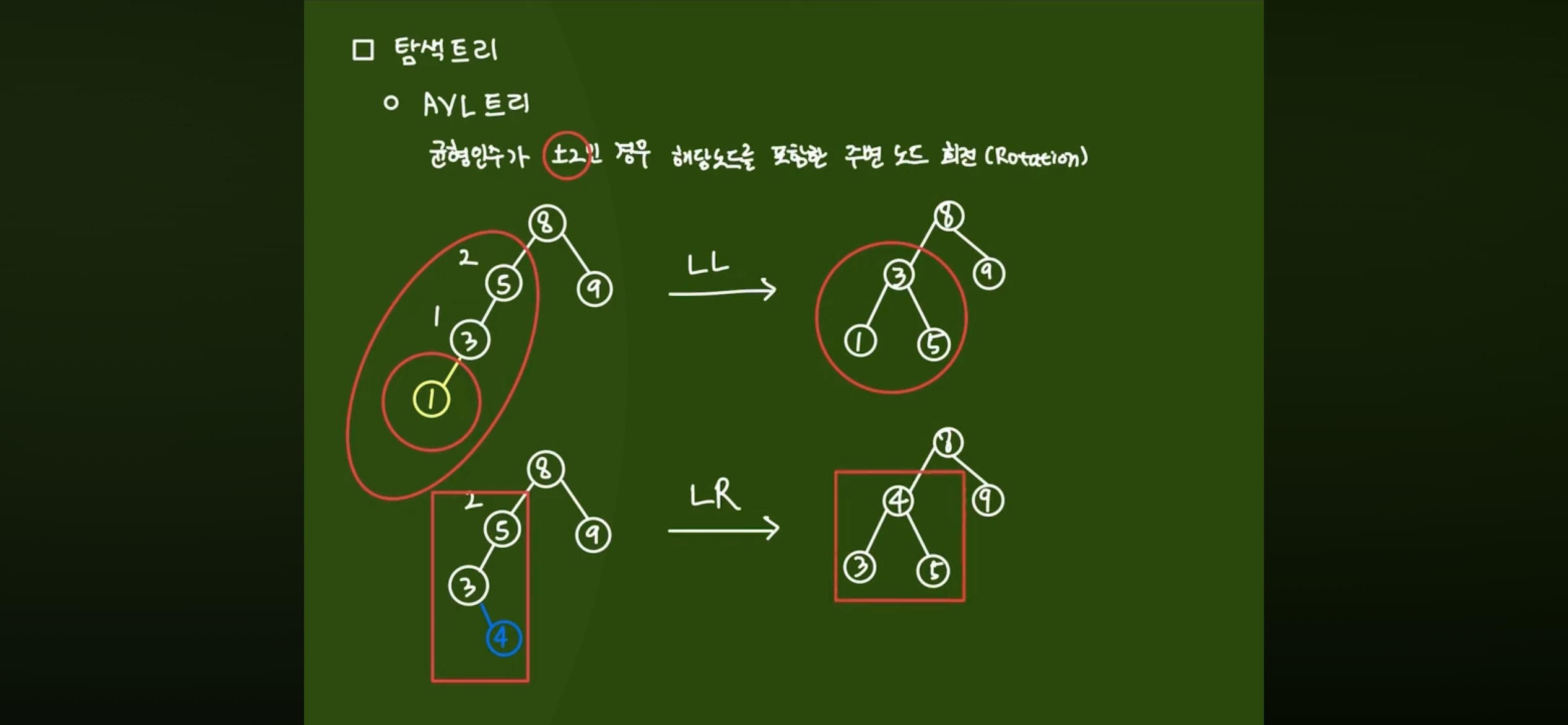
avl tree
youtube link
LL 은 right rotation
LR 은 left rotation 해서 LL 만들고 right rotation
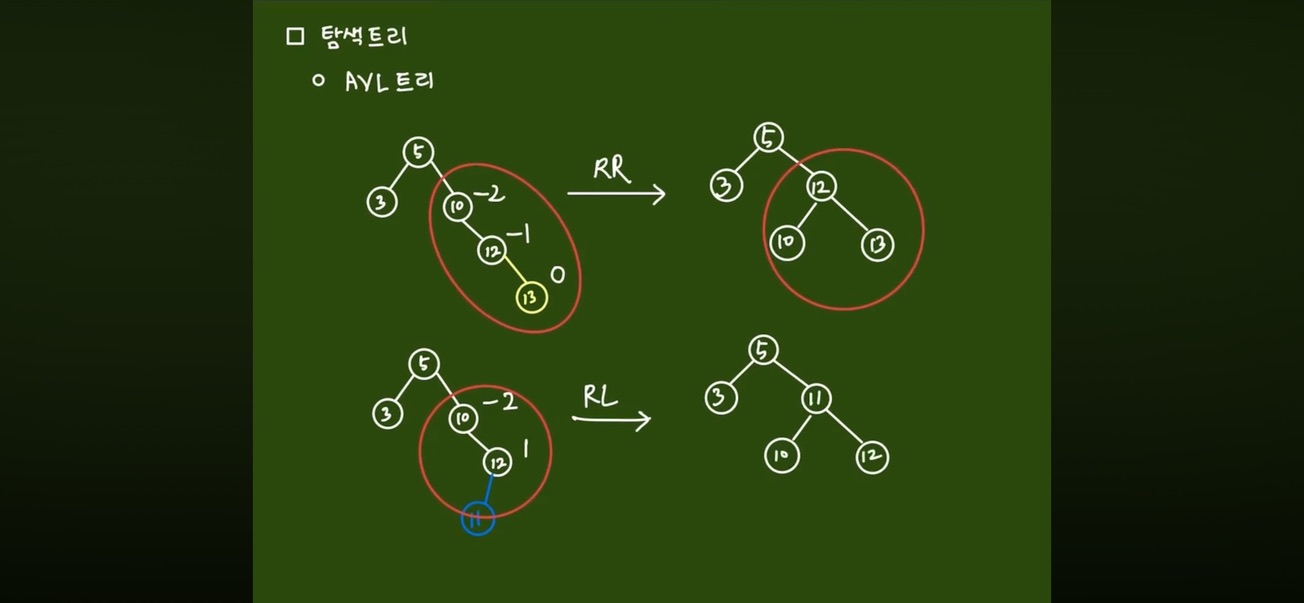
RR 은 left rotation
RL 은 right rotation 해서 RR 만들고 left rotation
concepts
AVL 트리란 서브트리의 높이를 적절하게 제어해 전체 트리가 어느 한쪽으로 늘어지지 않도록 한 이진탐색트리(Binary Search Tree)의 일종입니다. 트리의 높이가 ℎ일 때 이진탐색트리의 계산복잡성은 𝑂(ℎ) 이기 때문에 균형된 트리를 만들어 ℎ를 줄이고자 하는 발상에서 비롯됐습니다.
AVL 트리의 핵심 개념 가운데 하나가 Balance Factor(BF)입니다. 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 것입니다. 두 서브트리의 높이가 같거나 잎새노드라면 BF는 0입니다(empty tree의 BF는 -1로 정의).
Balance Factor(BF) : 왼쪽 서브트리 높이 - 오른쪽 서브트리의 높이
BF가 +2 혹은 -2인 인자가 포함 된 것만 회전(아래에서부터)
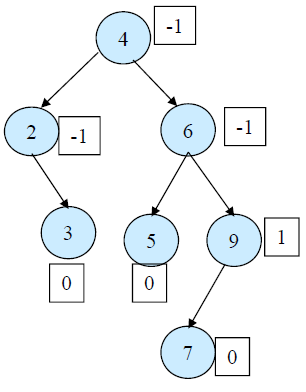
single rotation
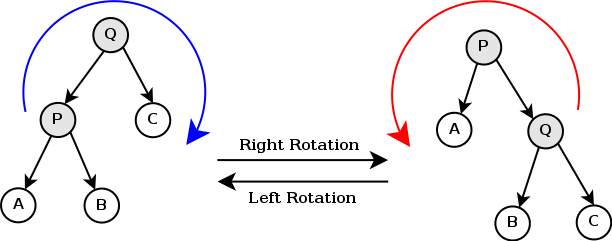
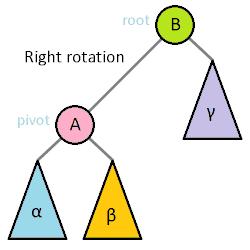
left rotation code(python)
def lrotate(self):
# 현재 트리의 기존 root를 A라고 두자
A = self.node
# 기존 root의 right child를 B라고 두자
B = self.node.right.node
# B의 left child(위 그림에서 베타)를 T라고 두자
T = B.left.node
# B를 새로운 root로 지정
self.node = B
# A를 root(B)의 새로운 left child로 지정
B.left.node = A
# T(위 그림에서 베타)를 A의 새로운 right child로 지정
A.right.node = T def rrotate(self):
A = self.node
B = self.node.left.node
T = B.right.node
self.node = B
B.right.node = A
A.left.node = Tdouble rotation
rotation 한 차례만으로 원하는 삽입 결과를 내지 못하는 케이스가 존재합니다. 다음 두 가지 경우 double rotation을 수행해 줍니다.
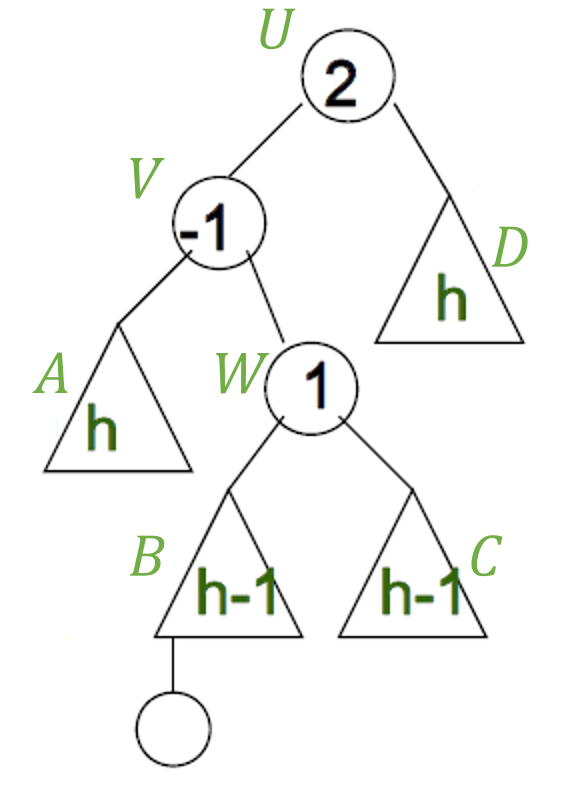
아래 그림과 같은 트리 구조에서 𝐵에 새로운 요소를 추가한다고 가정해 보겠습니다 (동그라미는 노드, 세모는 서브트리를 가리킵니다) 이렇게 되면 요소 하나를 삽입한 후의 𝑈, 𝑉, 𝑊의 BF는 각각 2, -1, 1이 됩니다. 따라서 𝑈를 루트노드로 하는 서브트리가 재구성 대상이 되겠습니다.
그런데 𝑉는 𝑈의 왼쪽 자식노드이고, 새 노드는 𝑉의 오른쪽 서브트리에 추가됐으므로 double rotation을 수행해 줍니다. 여기에서 𝑊는 𝑉의 오른쪽 자식노드입니다. 다음과 같습니다.
- 첫번째 : 𝑊를 중심으로 left rotation 수행 (𝐴를 잡아 당겨 내리는 과정)
- 두번째 : 𝑊를 중심으로 right rotation 수행 (𝐷를 잡아 당겨 내리는 과정)
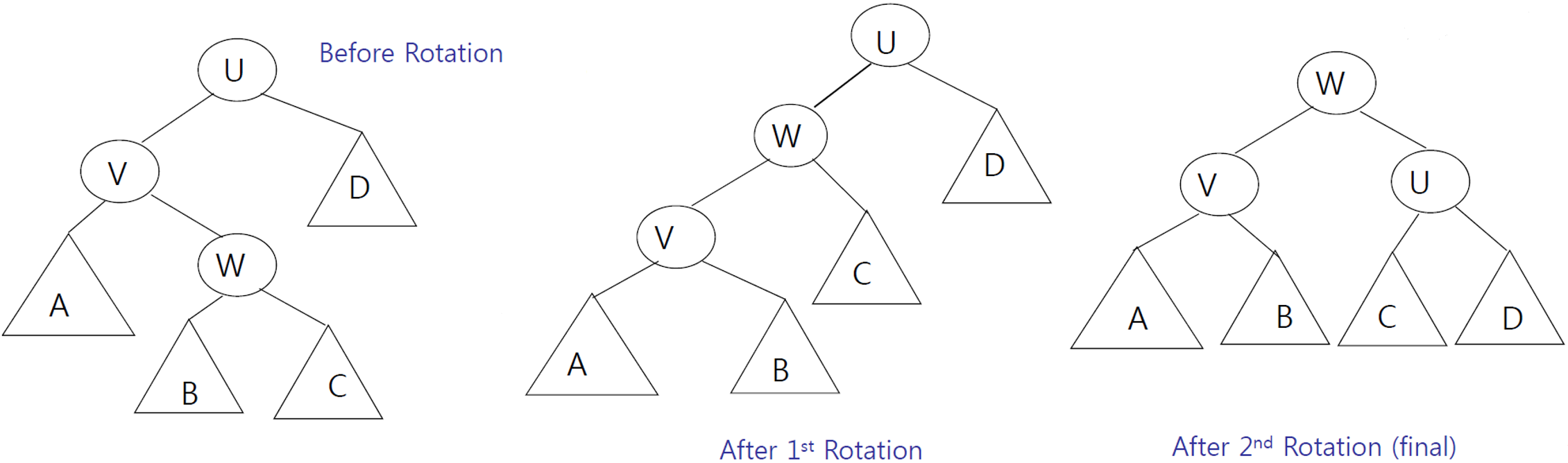
수행하고 나면 아래와 같은 모습입니다.
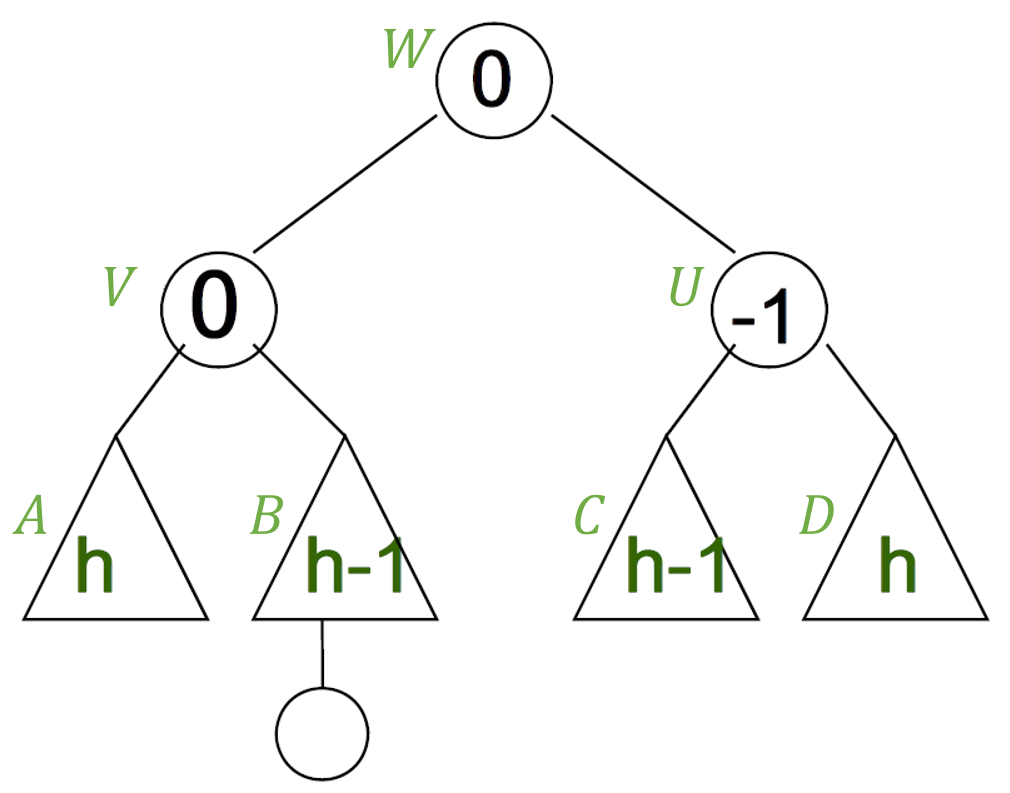
시나리오별 rotation
- 시나리오1 : 𝑈의 왼쪽 자식노드의 왼쪽 서브트리 𝐴에 새 노드 삽입 : single right rotation
- 시나리오2 : 𝑈의 왼쪽 자식노드의 오른쪽 서브트리 𝐵에 새 노드 삽입 : double rotation(left-right)
- 시나리오3 : 𝑈의 오른쪽 자식노드의 왼쪽 서브트리 𝐶에 새 노드 삽입 : double rotation(right-left)
- 시나리오4 : 𝑈의 오른쪽 자식노드의 오른쪽 서브트리 𝐷에 새 노드 삽입 : single left rotation
이를 구현한 파이썬 코드
def rebalance(self):
# 현재 노드(루트)~잎새노드에 이르는 경로의
# 모든 노드에 대해 Balance Factor 업데이트
self.update_heights(False)
self.update_balances(False)
# 현재 노드(루트, 위 그림에서 U)의 BF 절대값이 2 이상이면
# 불균형트리이므로 rotation 수행
while self.balance < -1 or self.balance > 1:
# U의 Balance Factor가 2 이상이면
# U의 왼쪽 서브트리 높이가 오른쪽보다 크므로
# 시나리오1 혹은 시나리오2에 해당
if self.balance > 1:
# U의 왼쪽 자식노드의 왼쪽 서브트리보다
# 오른쪽 서브트리의 높이가 클 경우 시나리오2에 해당
# 우선 single left rotation
if self.node.left.balance < 0:
self.node.left.lrotate()
# rotation이 됐으므로 BF 업데이트
self.update_heights()
self.update_balances()
# U의 왼쪽 자식노드의 왼쪽 서브트리가
# 오른쪽 서브트리보다 높이가 클 경우 시나리오1에 해당
# single right rotation (시나리오2도 이 작업 수행)
self.rrotate()
# rotation이 됐으므로 BF 업데이트
self.update_heights()
self.update_balances()
# U의 Balance Factor가 -1 이하이면
# U의 오른쪽 서브트리 높이가 왼쪽보다 크므로
# 시나리오3 혹은 시나리오4에 해당
if self.balance < -1:
# U의 오른쪽 자식노드의 오른쪽 서브트리보다
# 왼쪽 서브트리의 높이가 클 경우 시나리오3에 해당
# 우선 single right rotation
if self.node.right.balance > 0:
self.node.right.rrotate()
# rotation이 됐으므로 BF 업데이트
self.update_heights()
self.update_balances()
# U의 오른쪽 자식노드의 왼쪽 서브트리보다
# 오른쪽 서브트리보다 높이가 클 경우 시나리오4에 해당
# single left rotation (시나리오2도 이 작업 수행)
self.lrotate()
# rotation이 됐으므로 BF 업데이트
self.update_heights()
self.update_balances()coretime-c에서 const
https://modoocode.com/24
자세한건 여기 참고
int a = 13;
int* p = &a;
일 때
- const int* p 하면 포인터가 가르키는 값을 변경 못하게 하는거고,
- int* const p 하면 포인터를 변경 못하게 하는거
coretime- code review
- format, convention들을 팀에서 정한대로 하는거니까 지금은 없겠지만 그래도 한 가지로 정해서 일관성 있게 쓰자.
- 잘 쓴 코드는 코드별로 주석이 필요가 없다. 그렇지만 함수 위에 아래와 같이 간략하게 어떤 함수이고 어떤 파라미터를 가져오고 어떤 것을 리턴하는지 정도는 써주는 것이 좋겠다.
- 의사코드에서는 그냥 x,y,z이렇게 쓰지만 이름을 그대로 그렇게 가져다 쓰면 가독성이나 의미 전달이 어렵기 때문에 이름을 적절하게 바꿔주자.(지정해 준 것들을 제외하고)
-by Jungmin
/**
* @brief : 새로운 노드 node_t를 생성하고 0으로 초기화
* @param[in] t : 노드를 생성할 rbtree
* @param[in] key : 해당 노드의 키 값
* @return : 생성된 node_t의 포인터를 반환
*/
node_t *new_node(rbtree *t, const key_t key) {
node_t *new_node = (node_t *)malloc(sizeof(node_t));
new_node->parent = t->nil;
new_node->left = t->nil;
new_node->right = t->nil;
new_node->key = key;
new_node->color = RBTREE_RED;
return new_node;
}