
니모닉(Mnemonic)
- 메타마스크나 카이카스 같은 암호화폐 지갑을 복구하기 위한 값
- 단어 12개를 순서대로 나열하는 것으로 암호화
- 핵심은, 니모닉 자체는 개인키가 아님. 단순히 사람이 기억하기 쉽게 만든 백업 문장.
https://velog.io/@rlaekgks111/%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8-%EB%8B%88%EB%AA%A8%EB%8B%89Mnemonic
니모닉(Mnemonic) 생성방법
1. 엔트로피 생성
- 128, 160, 192, 224, 256비트 중 선택
엔트로피(Entropy)란?
- 무작위 비트의 집합
- 블록체인 지갑에는 예측 불가능한 값이 필요
- 예시: 128비트, 256비트 엔트로피
- 128비트: 2^128가지 경우의 수
- 256비트: 2^256가지 경우의 수
- 길이가 길수록 보안 강도는 높아짐.
2. 체크섬(checksum)추가
- 엔트로피를
SHA-256해시 함수에 넣고 실행 - 해당 결괏값의 상위 비트 일부를 체크섬으로 채택
3. 엔트로피 + 체크섬 합치기
- 128비트 엔트로피를 생성 했을 경우 + 4비트 체크섬 = 132비트
4. 11비트 단위로 나누기
- 132비트 / 11 비트 = 12개 단어
- 1개의 단어 당 11비트(2^11 = 0 ~ 2047 범위)
BIP-39단어 리스트에서 선택
BIP-39단어 리스트
ENG: https://github.com/bitcoin/bips/blob/master/bip-0039/english.txt
KOR: https://github.com/bitcoin/bips/blob/master/bip-0039/korean.txt
5. 니모닉 완성
- 총 12단어(11비트*12개 단어, 128비트) 생성 완료 128비트) 생성 완료
니모닉 생성 방법 요약
랜덤 엔트로피 (128~256비트)
│ SHA-256 체크섬 추가
▼
엔트로피 + 체크섬 비트열
│ 11비트씩 분할
▼
BIP-39 단어 매핑
▼
니모닉 12~24 단어 완성- 엔트로피 = 지갑 생성의 랜덤 재료
- 체크섬 = 입력 오류 방지용
- 11비트 단위 매핑 → 사람이 기억 가능한 단어 12~24개
- 하나의 니모닉으로 BIP-32/44 지갑 전체 복구 가능
시드(Seed)
- 니모닉은 사람이 기억하기 쉬운 단어 집합
- 그러나, 실제 지갑 키 생성 재료로는 사용 불가
- 즉, 안전한 512비트 짜리 시드(Seed)가 필요
- 그래서, 니모닉을 시드로 변환시키는 작업이 필요
[BIP-39] 니모닉 → 시드(Seed) 생성 방법
1. 니모닉 문장 + (선택) 패스프레이즈
패스프레이즈
- 25번째 단어라고 불림.
- 그저 단어 하나 혹은 다른 문장을 추가하는 것
2. PBKDF2-HMAC-SHA512 함수를 2048회 반복
PBKDF2(Password-Based Key Derivation Function 2)
- 비밀번호나 니모닉을 안전한 암호키로 바꿔주는 함수
- 설탕(니모닉)을 여러 번 녹여서 단단한 설탕 블록(시드) 만드는 법
HMAC-SHA512
HMAC= Keyed-Hash Message Authentication Code
- “비밀 키와 메시지를 합쳐서 생성하는 해시”
SHA512= 해시 함수, 출력 512비트(64바이트)
HMAC 계산 방법
HMAC(key, message) = SHA512((key ⊕ opad) || SHA512((key ⊕ ipad) || message)) // key: 비밀 키 (시드 등) // message: 입력 메시지 // ⊕ : XOR 연산 // opad: 0x5c 반복, ipad: 0x36 반복 (64바이트) // || : 연결(concatenation)
3. 시드(seed) 생성
그럼 BIP-39는 니모닉 ⇌ 시드 변환 과정인걸까?
-
답은 YES
-
BIP = Bitcoin Improvement Proposal
- 비트코인 개선안, 표준화 문서 번호
-
BIP마다 고유 번호 부여
예:
BIP-32: HD 지갑(Key Derivation)
BIP-44: 다중 코인/계층 구조
BIP-39: 니모닉 → 시드 변환 -
즉, “39”는 그냥 순서 번호일 뿐, 기술적 의미나 암호학적 의미는 없음
마스터키(Master Key)
- 시드(Seed)에서 최초로 생성되는 루트 확장 개인키(root extended private key)
- 총 64바이트(512비트)로 개인키 32B + 체인코드 32B + 메타데이터로 구성
- 체인코드와 함께 자식키(개인키) 생성 가능
개인키(Private Key)
- 블록체인 자산을 제어할 수 있는 비밀 번호
- 256비트의 정수
- 절대 공개되면 안 됨(공개될 경우 누구든 해당 코인 이동 가능!)
- 해당 정수값(개인키)를 타원 곡선 암호(ECDSA, secp256k1)에 넣으면 공개키가 계산됨.
- 마스터키와 다르개 자식키 생성 불가. 이미 본인이 자식임.
개인키와 공개키에 대한 설명이 필요하다면?
BIP-32
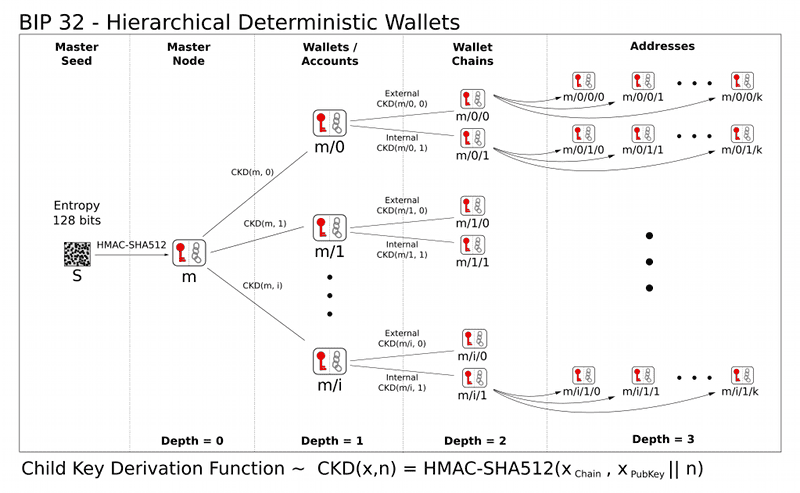
- 계층적 결정적 지급(HD Wallet, Hierarchical Deterministic Wallet)을 정의한 표준
- 시드 하나만 있으면 무한히 많은 개인키·공개키를 체계적으로 파생할 수 있게 해주는 규칙.
- 즉, BIP-32는 시드에서 마스터키를 만들고, 그 마스터 키에서 체계적으로 개인키들을 파생하는 표준 규격 문서
- 시드 → 마스터키 → (여러) 개인키
💡 비유:
시드 = "나무의 씨앗"
마스터키 = "나무 줄기"
자식 개인키들 = "가지와 잎들"
https://trezor.io/learn/advanced/standards-proposals/what-is-bip32
[BIP-32 1단계] 시드 → 마스터키(Master Key) 생성
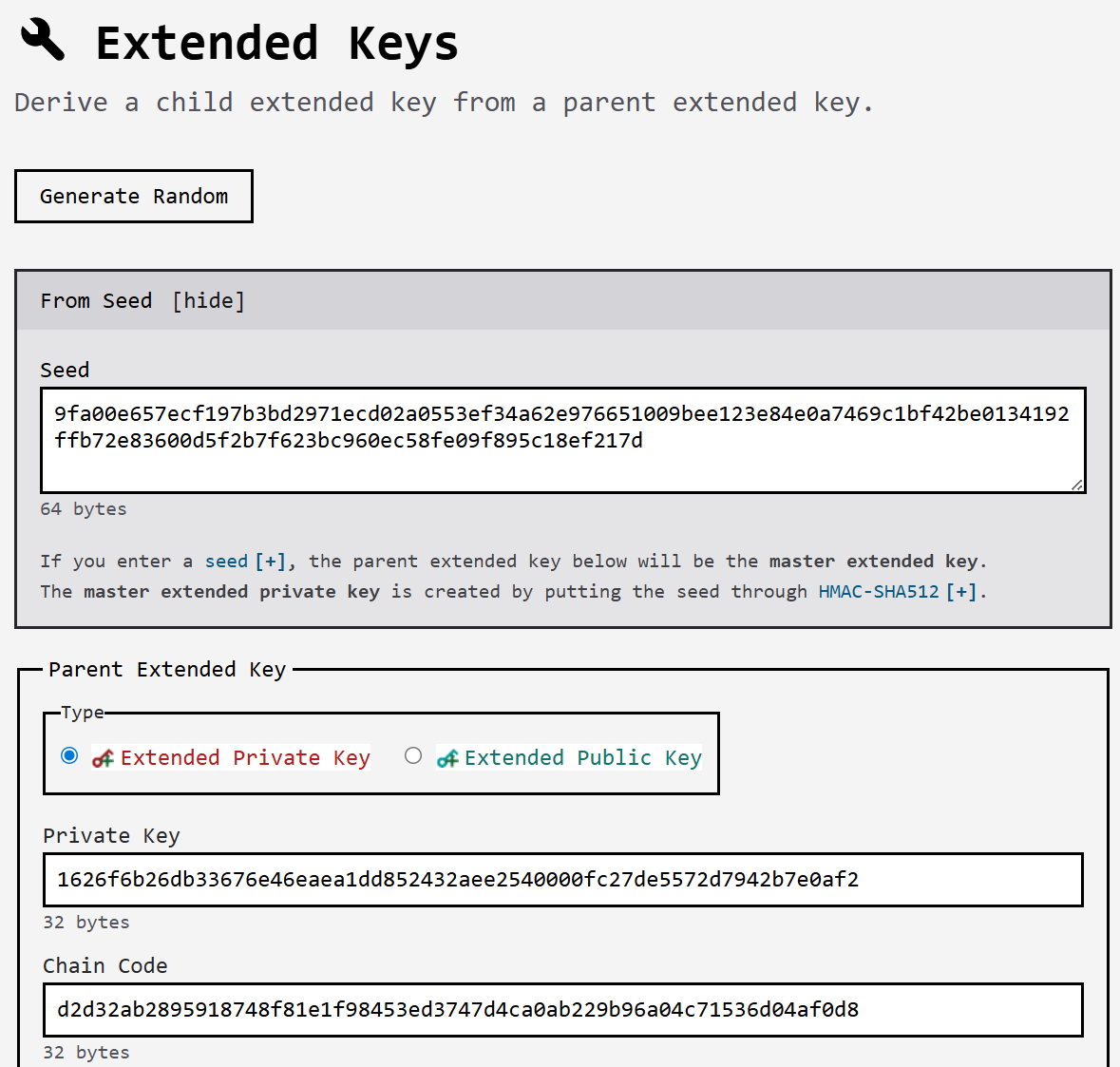
1. 시드에 HMAC-SHA512 실행
- 512비트(64B)의 시드에 HMAC-SHA512 실행
- (1)번 실행에 대한 결과: 512비트
- 결과의 앞 32바이트: 마스터 개인키(m)
- 결과의 뒤 32바이트: 체인코드(chain code)
Ref. https://learnmeabitcoin.com/technical/keys/hd-wallets/extended-keys/
2. 마스터 확장 개인키(Xprv, eXtended PRiVate key) 생성
| 필드 | 길이 | 설명 |
|---|---|---|
| 버전 | 4바이트 | xprv용 고유값 |
| 깊이(Depth) | 1바이트 | 트리 레벨 (0=마스터) |
| 부모 지문 | 4바이트 | 부모 공개키 지문 |
| 자식 번호 | 4바이트 | CKD에서 사용된 인덱스 |
| 체인코드 | 32바이트 | 키 파생용 HMAC 값 |
| 개인키 | 32바이트 | 실제 마스터 개인키 값 |
| 체크섬 | 4바이트 | Base58Check 체크 |
- 합치면 총 78바이트
3. Xprv를 Base58Check로 인코딩
Base58Check를 통한 인코딩 진행- 총 111자로 변환
- 즉, 내부는 78바이트이지만, base58Check를 통해 111자로 바꿔 읽기 편하게 한 것
정리
- 64바이트 시드는 마스터 키를 만들기 위한 재료
- 시드에 HMAC-SHA512를 실행하여 마스터 개인키와 체인코드를 취득
- Xprv(마스터 개인키 + 체인코드 + 메타데이터, 약 78바이트) 생성
- Xprv를 Base58Check로 인코딩해서 읽기 쉬운 111문자로 변환
[BIP-32 2단계] 마스터키 → 자식키 파생 (CKD, Child Key Derivation)
1. HMAC 입력 준비(Non-Hardended, 일반 경우)
- HMAC 키 = 부모의 32바이트 체인코드
- HMAC 데이터 = 부모의 33바이트 공개키
+) 부모의 공개키가 33바이트 인 이유
- 타원공선의 공개키는 (x, y)의 좌표 쌍으로
- x, y는 각각 32B -> 총 64B
- 그러나 ECC에서는 x좌표만 있다면, y좌표의 절댓값을 알 수 있고,
- 1비트를 추가하여 y의 홀/짝 여부만 표시하면
- 32B + 1b로 절약 가능
- 단, 접두사는 1B로 규정하도록 Secp256k1 규격에 정의되어 있으므로 1바이트로 늘려서 정의
- 짝수: 0x002, 홀수: 0x03
- 결론: 접두사 1B + X좌표 32B = 33B 짜리 압축 공개키 생성 가능
2. HMAC-SHA512 수행
- 결과 64B
- 앞 32B(IL): 자식 개인키 계산 재료
- 뒤 32B(IR): 자식 체인 코드
3. 자식 개인키 계산
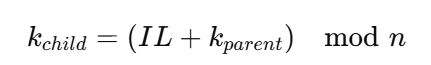
- n = secp256k1 곡선 order
- IL을 부모 키에 더해서 새로운 자식 개인키 생성
4. 자식 Xprv 만들기
- 자식 xprv = 확장 개인키 (78B 구조)
| 필드 | 길이 | 설명 |
|---|---|---|
| 버전 | 4바이트 | xprv용 |
| 깊이(Depth) | 1바이트 | 부모 Depth+1 |
| 부모 지문 | 4바이트 | 부모 공개키 지문 |
| 자식 번호 | 4바이트 | i |
| 체인코드 | 32바이트 | IR |
| 개인키 | 32바이트 | k_child(자식 개인키) |
| 체크섬 | 4바이트 | Base58Check 체크 |
- 이후 Base58Check 인코딩(111문자)
BIP-32 요약
HD Wallet & CKD (Child Key Derivation)
- BIP-32 = Hierarchical Deterministic Wallet(HD Wallet) 규격
- 한 마스터 키(xprv)로 무한히 자식 키 파생 가능
- 자식 키 = 개인키 + 체인코드 → 안전하게 트리 구조로 관리
BIP-32 특징
- 한 마스터 시드로 무한히 자식 키 생성 가능
- 체인코드 + HMAC → 자식 키 안전하게 독립적 파생
전체 흐름 정리
[니모닉 12~24단어]
│ (BIP-39 PBKDF2)
▼
[시드(seed, 64B)]
│ (BIP-32 HMAC-SHA512)
▼
[마스터 개인키(xprv) + 체인코드]
│
├─> [자식 개인키 1] → 공개키 1 → 주소 1
├─> [자식 개인키 2] → 공개키 2 → 주소 2
└─> [자식 개인키 3] → 공개키 3 → 주소 3
│ (BIP-44 경로 표준 적용)
▼
[무한히 많은 지갑 주소 생성 가능]- 니모닉 하나만 있으면 지갑 전체 복구 가능
- 패스프레이즈를 추가하면 다른 지갑으로 분리 가능
- xpub만 있어도 입금용 주소 생성 가능, 출금은 불가
